当前位置：首页 > news >正文

代码随想录刷题Day43

news 2025/8/28 12:53:23

二叉搜索树中的众数

这道关于二叉搜索树的众数求解，还是基于二叉搜索树的遍历来完成的，一边遍历，一边计数比较当前该值出现的次数是否是最多的次数：

class Solution {
public:map<int,int> treecnt;int max_cnt= 1;vector<int> ans;void dfs(TreeNode* root){//深度遍历if(!root) return;else{if(treecnt.find(root->val)==treecnt.end()){//该值第一次出现treecnt[root->val] = 1;}else{//该值已经出现过treecnt[root->val]++;}if(treecnt[root->val]>max_cnt){//出现的次数超过max_cnt，ans中的值重新清除，max_cnt也更新max_cnt = treecnt[root->val];ans.clear();ans.push_back(root->val);}else if(treecnt[root->val]==max_cnt){//当前的值出现的次数与max_cnt一样，则放入ans中ans.push_back(root->val);}//孩子节点处理   if(root->left) dfs(root->left);if(root->right) dfs(root->right);}}vector<int> findMode(TreeNode* root) {dfs(root);return ans;}
};

这道题，感觉搜索二叉树的中序遍历递增的性质没能用上，只好当普通的二叉树求众数来求解。

二叉树的最近公共祖先

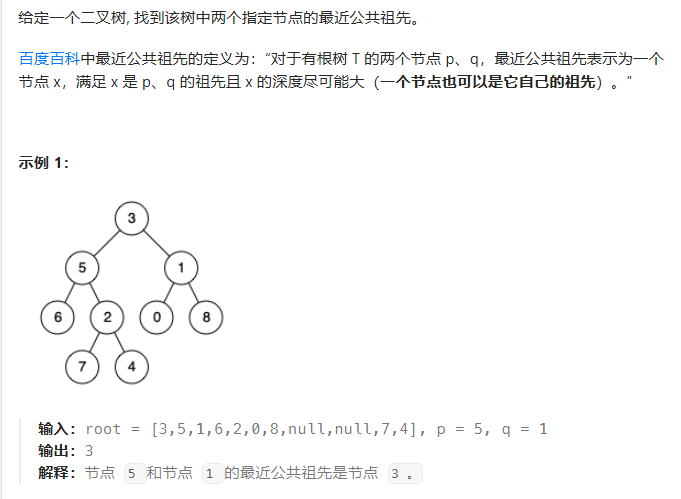
LCA问题是比较经典的题目了，但是自己还是一时间忘记怎么做了。之前学数据结构的时候，学习的方法是用数组的方式构造的树。基本思路是，先确定要找到p和q在哪两层，把两个层数先统一一下，再开始同步向根的方向递减，直到寻找的方向交汇，则停止查找：

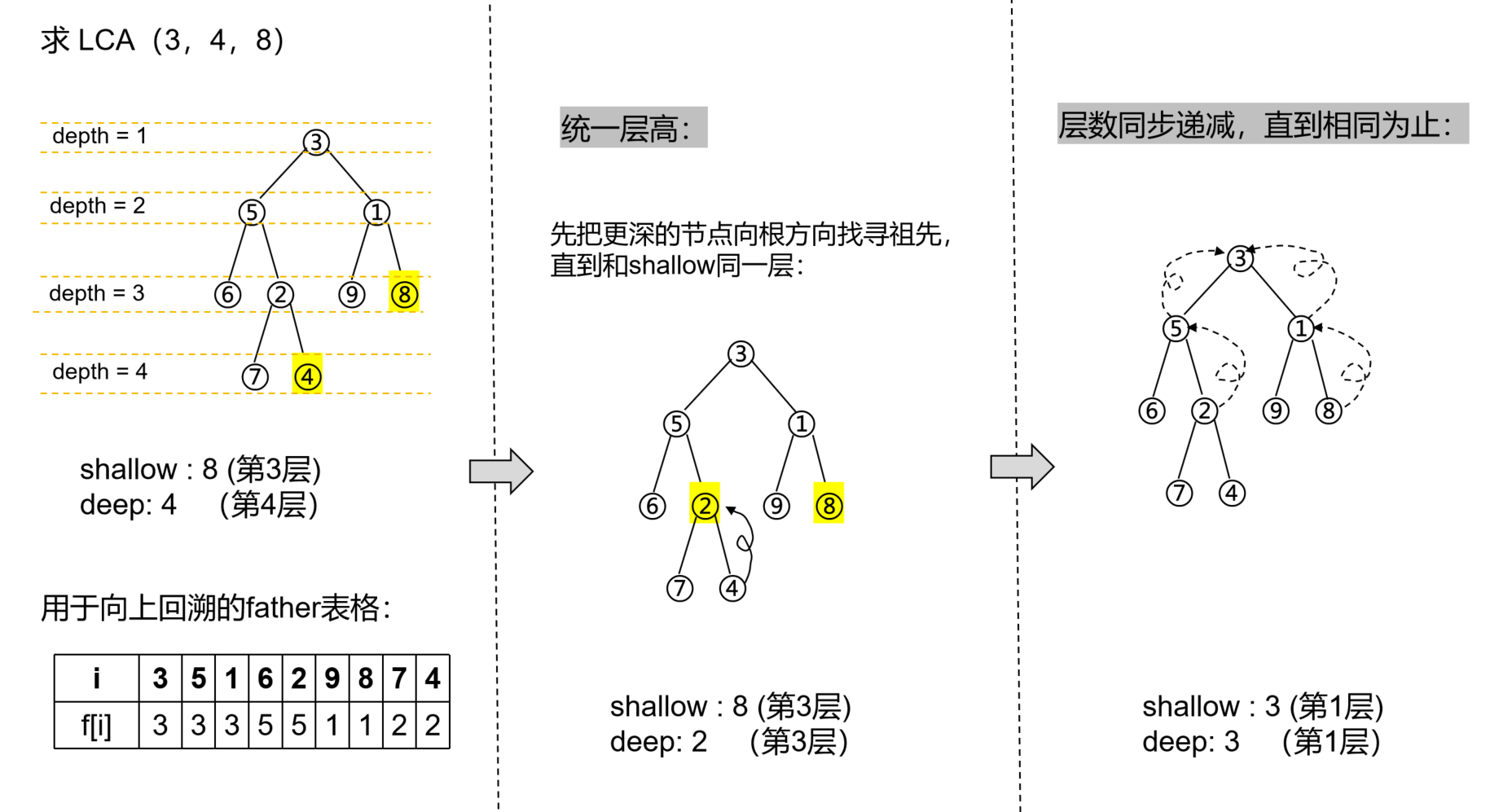
对应的代码如下：

class Solution {
public:TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {queue<TreeNode*> queueTree;queueTree.push(root);map<TreeNode*,int> nodeDepth;map<TreeNode* ,TreeNode*> fatherNode;int depth = 1;int queue_size = 1;TreeNode* tmp;//初始化queueTree.push(root);nodeDepth[root]=depth;fatherNode[root]=root;//层序遍历，确定节点深度，以及father关系while(!queueTree.empty()){queue_size = queueTree.size();while(queue_size--){tmp = queueTree.front();queueTree.pop();nodeDepth[tmp] = depth;if(tmp->left){fatherNode[tmp->left] = tmp;queueTree.push(tmp->left);}if(tmp->right){fatherNode[tmp->right] = tmp;queueTree.push(tmp->right);}}depth++;}//让两个节点设置到同一深度TreeNode* shallow;TreeNode* deep;if(nodeDepth[p]==nodeDepth[q]){shallow = p;deep = q;}else if(nodeDepth[p]<nodeDepth[q]){shallow = p;deep = q;}else if(nodeDepth[p]>nodeDepth[q]){shallow = q;deep = p;}while(nodeDepth[shallow]!= nodeDepth[deep]){deep = fatherNode[deep];}//从同一深度开始沿着根的方向找if(shallow == deep) return shallow;while(fatherNode[deep]!=fatherNode[shallow]){deep= fatherNode[deep];shallow = fatherNode[shallow];}return fatherNode[deep];}
};

但是这种方法时空消耗较多，查看代码随想录的参考思路，知道了回溯的递归解决方法：

后序遍历的处理方式
先从左子树和右子树查看是否可以找到p和q，如果可以，则返回找到的p或者q节点；如果没有找到则返回空节点
接着是根据左右子树的查询情况来判断当前节点左右子树查找情况，如果都找到了，那么当前节点就是答案，但如果不是，就继续回溯，直到某个节点两个子树找到了p和q为止。

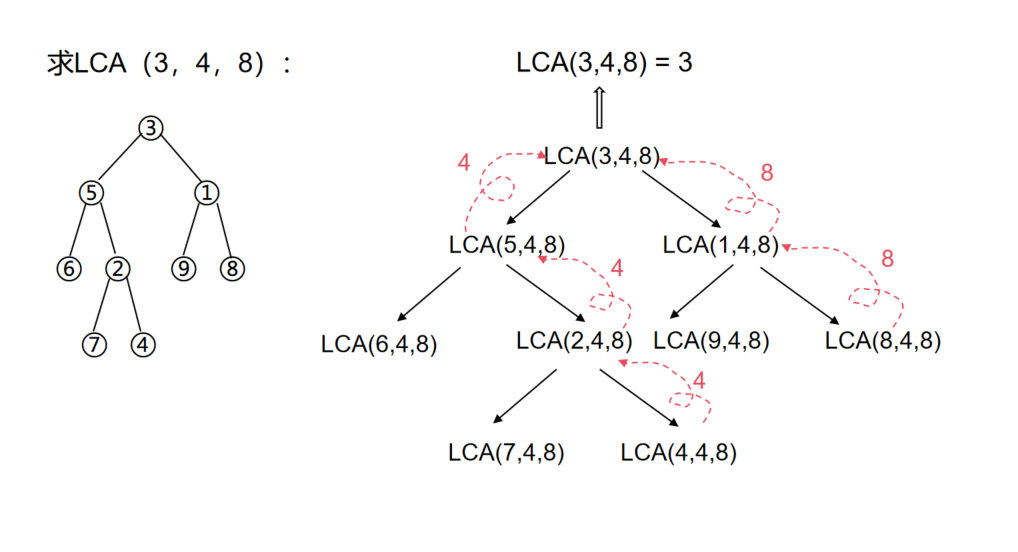
如上，先从根节点往叶子节点扩展递归，然后是从找到的节点开始往根节点回溯找到的答案，直到某个节点的左右子树都找到了p和q，返回结果。

class Solution {
public:TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {//递归的终止条件是：要么找到p或者q,要么是从空树中找节点if(root==p||root==q||root==nullptr) return root;//沿着左子树找p或者q,返回找寻结果，如果是空说明没找到，如果非空表示找到了TreeNode* left = lowestCommonAncestor(root->left,p,q);//沿着右子树找p或者q，如果空则说明没找到，如果非空表示找到了TreeNode* right = lowestCommonAncestor(root->right,p,q);if(left ==nullptr && right==nullptr){return nullptr;}else if(left == nullptr && right != nullptr){//右子树找到一个节点return right;}else if(left != nullptr && right == nullptr){//左子树找到一个节点return left;}else{//左右子树中正好找到了p,q.return root;}}
};

这个递归思路对自己来说还是有些难想到。递归分为三部分：