DFT、CHORD
DFT (Dynamic Fine-Tuning)
来自 ON THE GENERALIZATION OF SFT: A REINFORCEMENT LEARNING PERSPECTIVE WITH REWARD RECTIFICATION(https://arxiv.org/abs/2508.05629),中文版介绍可以参考https://mp.weixin.qq.com/s?__biz=MzkxNTU5NDM4Mg==&mid=2247485349&idx=1&sn=4dc110ffc2ca356959547bf51603ce74&chksm=c05bfa1784226f3b775834e9c37e30028c899b2aeaf5c7299a97bbb4bfc52603315b2f19d24f#rd

DFT的梯度如下公式,梯度绝对值正比于∇θπθ(yt⋆∣y<t⋆,x)\nabla_{\theta} \pi_{\theta}(y_{t}^{\star} \mid y_{<t}^{\star}, x)∇θπθ(yt⋆∣y<t⋆,x),也就是next tokens predictions的概率越大,梯度越大。模型倾向于学习Demonstrations中梯度较大的解,也就是和原模型输出pattern差异较大的冷门解,而忽略了常规性。
∇θLDFT(θ)=E(x,y⋆)∼D[−∑t=1∣y⋆∣sg(πθ(yt⋆∣y<t⋆,x))πθ(yt⋆∣y<t⋆,x)∇θπθ(yt⋆∣y<t⋆,x)]\nabla_{\theta} \mathcal{L}_{\text{DFT}}(\theta) = \mathbb{E}_{(x, y^{\star}) \sim \mathcal{D}} \left[ - \sum_{t=1}^{|y^{\star}|} \frac{\text{sg} \left( \pi_{\theta}(y_{t}^{\star} \mid y_{<t}^{\star}, x) \right)}{\pi_{\theta}(y_{t}^{\star} \mid y_{<t}^{\star}, x)} \nabla_{\theta} \pi_{\theta}(y_{t}^{\star} \mid y_{<t}^{\star}, x) \right]∇θLDFT(θ)=E(x,y⋆)∼D−t=1∑∣y⋆∣πθ(yt⋆∣y<t⋆,x)sg(πθ(yt⋆∣y<t⋆,x))∇θπθ(yt⋆∣y<t⋆,x)
DFT的缺陷如下“Based on our evaluations and community feedback, DFT performs strongly on tasks with non-deterministic solution trajectories—i.e., those that admit multiple valid reasoning paths—such as mathematical chain-of-thought (CoT) reasoning, solutions to highly complex coding problems, and multimodal reasoning with informative CoT. By contrast, its performance is weaker on tasks with a single, well-specified ground-truth answer, particularly when the associated CoT (if exists) is highly constrained and near-deterministic (low-entropy).”,摘录自https://github.com/yongliang-wu/DFT,也就是说更开放的问题上,DFT的效果才会更好
CHORD
来自阿里的论文 ON-POLICY RL MEETS OFF-POLICY EXPERTS: HARMONIZING SUPERVISED FINE-TUNING AND REINFORCEMENT LEARNING VIA DYNAMIC WEIGHTING(https://arxiv.org/pdf/2508.11408),实际上是对上述DFT的改进

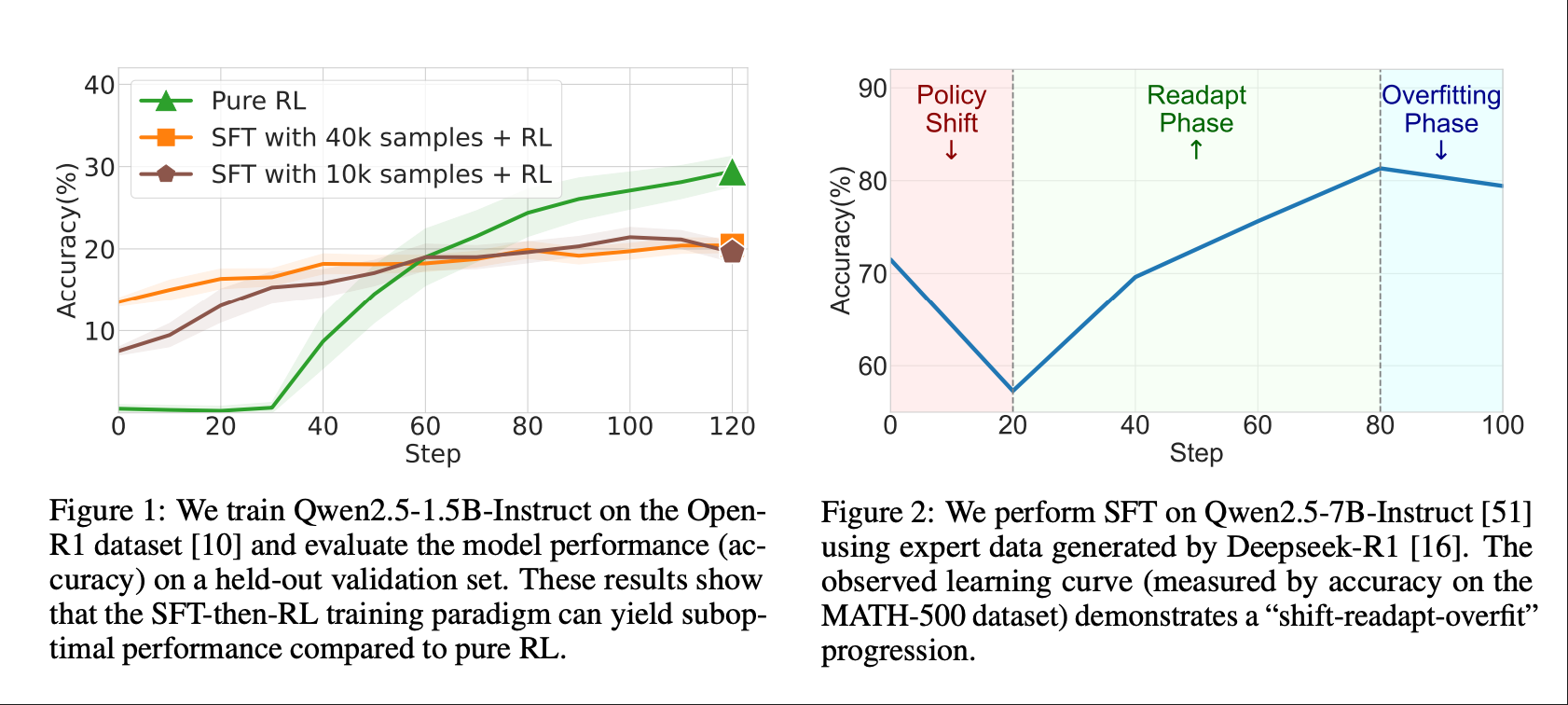
一句话来说就是把SFT的loss和RL的loss通过参数u来加起来,但是直接u*sft_loss+(1-u)*grpo_loss,同时u刚开始给的大一些,还是会出现上图中ReAdapt phase的问题,如Figure 4所示:
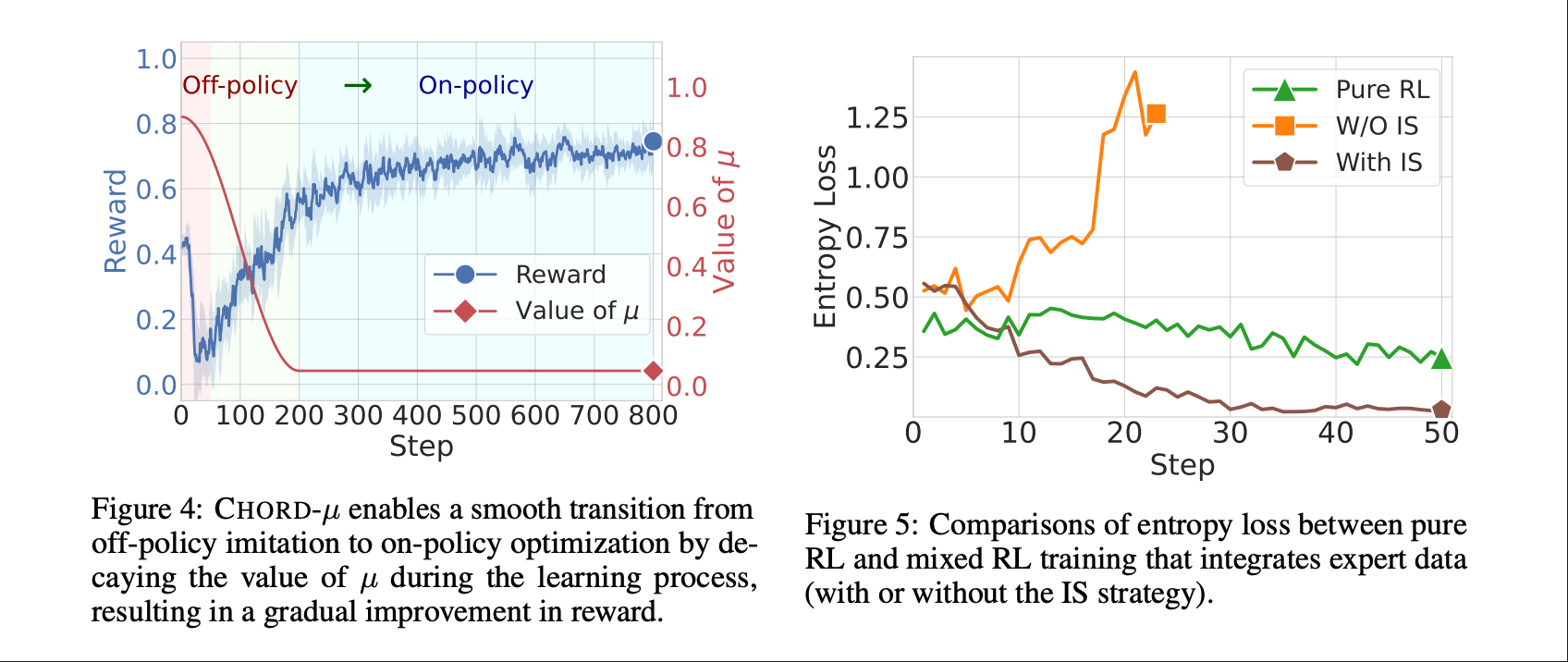
作者为了平滑ReAdapt phase的问题,尝试了两种方法。第一种方法是上述Figure 5里的With IS(Importance Sampling),也就是下图公式(4)

但是公式(4)的做法并不理想,导致Figure 5中的熵迅速下降。造成这种现象的原因是上述DFT部分分析的,所以要down-weighting the learning signal for tokens at both ends of the probability spectrum

