代码随想录刷题Day42

验证二叉搜索树

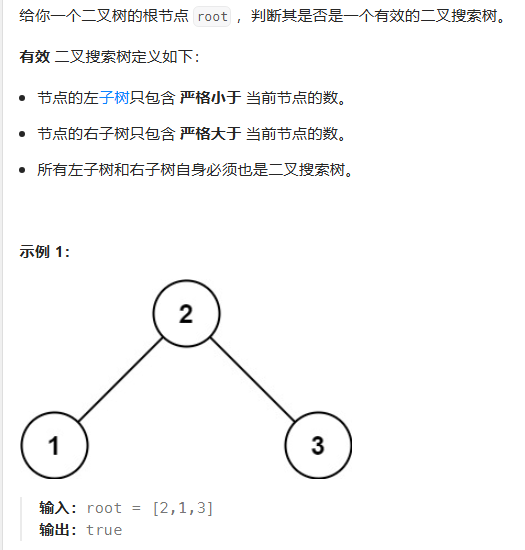
这道题我第一想法是按照题目给出的定义递归写代码：

class Solution {
public:bool isValidBST(TreeNode* root) {if(!root) return true;else if(!root->left && !root->right){//叶子节点return true;}else if(root->left && !root->right){//只有左子树if(root->left->val < root->val){return isValidBST(root->left);}else return false;}else if(root->right && !root->left){//只有右子树if(root->right->val > root->val){return isValidBST(root->right);}else return false;}else{//左右子树都存在if(root->left->val < root->val && root->val < root->right->val){return isValidBST(root->left) && isValidBST(root->right);}else return false;}}
};

但是这样写还是存在一些例子无法通过：

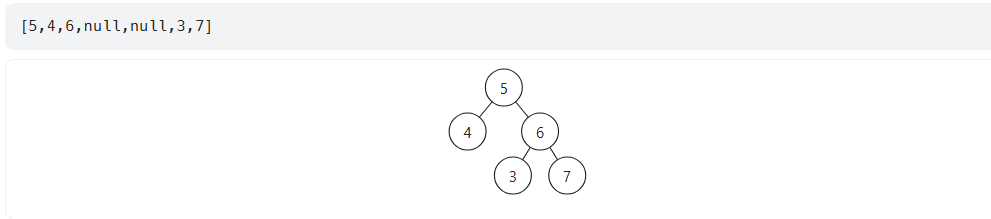
这个例子被卡住，是因为5的右子树上的节点3比根节点5小，虽然在左节点-根节点-右节点这样的结构上，满足定义要求，但是从整体上看，只满足三节点的严格递增关系的子树组成的二叉树并不满足要求。在比较大小上，只比较根节点还不够，但是自己又想不出细节。只好看代码随想录参考题解。

原来使用中序遍历就行了，中序遍历之后查看获得的序列是否是严格递增的就好。

class Solution {
public:bool isValidBST(TreeNode* root) {//中序遍历stack<TreeNode*> stackTree;vector<int> InorderRes;stackTree.push(root);TreeNode* cur = root;while(!stackTree.empty()){if(cur!=nullptr){//左孩子入栈if(cur->left) stackTree.push(cur->left);cur = cur->left;}else{cur = stackTree.top();stackTree.pop();InorderRes.push_back(cur->val);if(cur->right) stackTree.push(cur->right);cur = cur->right;}}//查看中序遍历结果是否严格递增int len = InorderRes.size();for(int i = 0;i<len-1;i++){if(InorderRes[i]>=InorderRes[i+1]) return false;}return true;}
};

二叉搜索树的最小绝对差

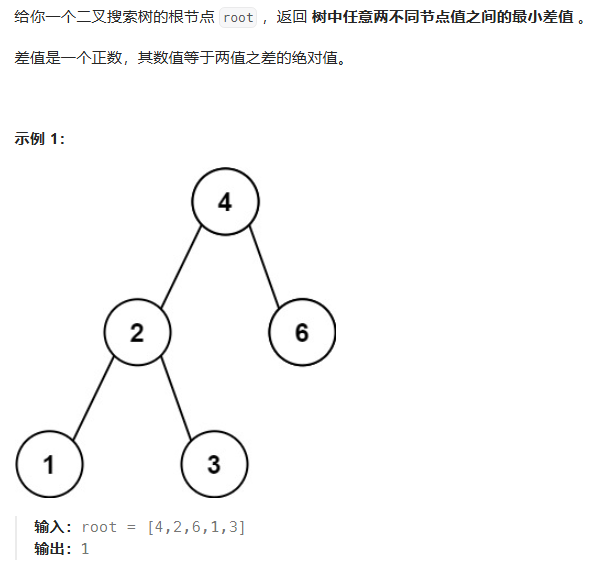
这道题基于对二叉搜索树的解法，对中序遍历的结果，找出相邻两个元素之间的最小差值即可：

class Solution {
public:int getMinimumDifference(TreeNode* root) {//中序遍历获得遍历序列stack<TreeNode*> stackTree;vector<int> InorderVec;TreeNode* cur;stackTree.push(root);cur = root;while(!stackTree.empty()){if(cur){if(cur->left) stackTree.push(cur->left);cur  = cur -> left;}else{cur = stackTree.top();stackTree.pop();InorderVec.push_back(cur->val);if(cur ->right) stackTree.push(cur->right);cur = cur->right;}}//找相邻两个节点之间的差值int dif = 100001;int len = InorderVec.size();for(int i = 0;i<len-1;i++){if(abs(InorderVec[i+1]-InorderVec[i])<dif){dif = abs(InorderVec[i+1]-InorderVec[i]);}}return dif;}
};

这两道题，一句话总结，即，二叉搜索树的验证或者关于值的处理可以使用中序遍历来解决。