骰子滚出最大和

题目背景

本题目来自仓库 https://github.com/Disposrestfully/CCPC-CQ-2024/tree/main

题目描述

在 n 行 m 列的网格的最左上角的格子上，有一个边长和网格格子边长相等的骰子。初始，这个骰子 1 在顶面，2 朝前，3 朝右，i 的背后是 7−i，如下图所示。

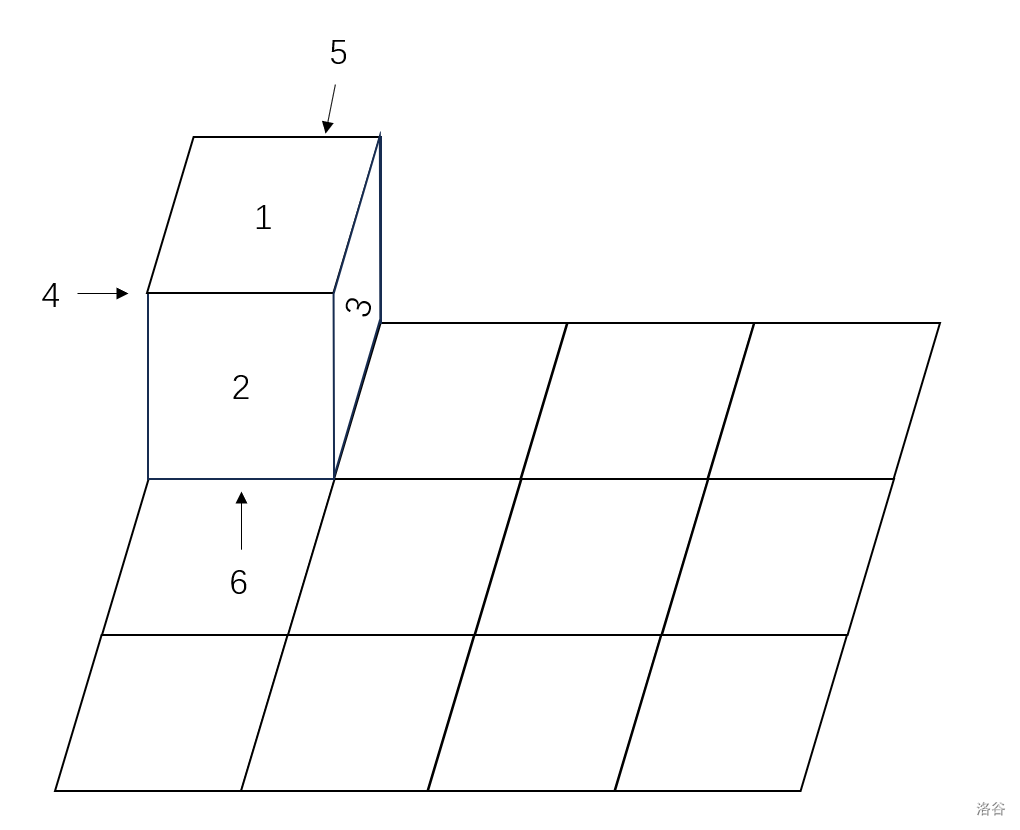
现在你可以做任意多次操作，每次操作为以下两种：

• 若当前骰子所在的格子没有数字，在这个格子上写下骰子底面的数字；
• 选择上下左右四个方向的某一个，将骰子沿着这个方向滚一次：选择骰子底面对应方向的棱，将骰子沿着这条棱旋转九十度。下图展示了初始状态向右滚一次的结果。你不能将骰子滚出网格。

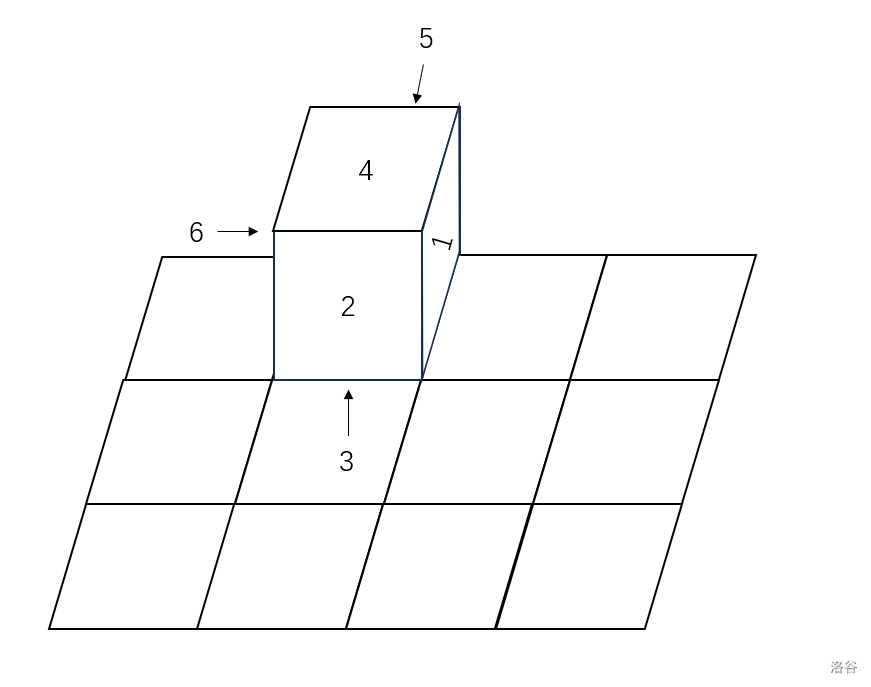
注意：你可以在骰子经过一个没有数字的格子时选择不在这个格子上写下骰子底面的数字。

你希望最大化最后网格上所有写过数字的格子的数字的和。

输入格式

输入一行两个整数 n,m (2≤n,m≤1000)，表示网格的长和宽。

输出格式

输出一行一个整数，表示在进行任意多次操作后，网格上所有写过数字的格子的数字的和的最大值。

输入输出样例

输入 #1复制

2 2

输出 #1复制

24

思路

因为骰子中，最大的数是 6，所以我们就要尽可能使尽可能多的格子上的数字为 6。

因为 n 和 m 都是大于等于 2 的，也就说说骰子一定可以经过滚动，将所有的格子都覆盖为 6

那我们就将所有的格子都覆盖为 6，就是最大值了，最后答案就是 n×m×6

源代码

#include<bits/stdc++.h>

using namespace std;

int n,m;//用long long比较好

int main()

{

cin>>n>>m;

cout<<n*m*6<<endl;

return 0;

}