LeetCode-221. 最大正方形

1、题目描述

在一个由 '0' 和 '1' 组成的二维矩阵内，找到只包含 '1' 的最大正方形，并返回其面积。

示例 1：

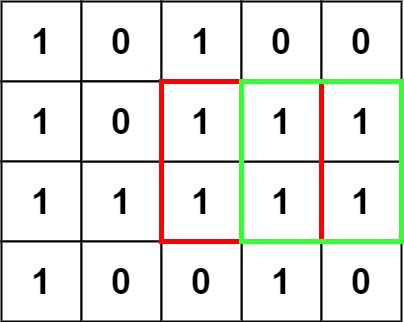
输入：matrix = [["1","0","1","0","0"],["1","0","1","1","1"],["1","1","1","1","1"],["1","0","0","1","0"]]
输出：4

示例 2：

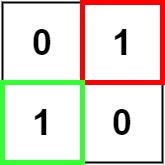
输入：matrix = [["0","1"],["1","0"]]
输出：1

示例 3：

输入：matrix = [["0"]]
输出：0

提示：

• m == matrix.length
• n == matrix[i].length
• 1 <= m, n <= 300
• matrix[i][j] 为 '0' 或 '1'

---

2、代码

class Solution
{
public:int maximalSquare(vector<vector<char>>& matrix) {// 边界条件：如果矩阵为空或第一行为空，直接返回0if(matrix.empty() || matrix[0].empty()) return 0;// 获取矩阵的行数和列数int row = matrix.size();int col = matrix[0].size();// 创建DP数组：dp[i][j]表示以(i,j)为右下角的最大正方形的边长vector<vector<int>> dp(row, vector<int>(col, 0));// 记录最大正方形的边长int max_sid = 0;// 遍历矩阵中的每个元素for(int i = 0; i < row; ++i){for(int j = 0; j < col; ++j){// 只处理值为'1'的单元格（可能构成正方形的一部分）if(matrix[i][j] == '1'){// 边界情况：第一行或第一列的'1'最多只能形成1x1的正方形if(i == 0 || j == 0){dp[i][j] = 1;}else{// 非边界情况：当前单元格的最大正方形边长由三个方向决定int up = dp[i - 1][j];       // 上方单元格的最大边长int left = dp[i][j - 1];     // 左侧单元格的最大边长int up_left = dp[i - 1][j - 1]; // 左上方单元格的最大边长// 取三个方向的最小值加1，确保能形成正方形dp[i][j] = min(min(up, left), up_left) + 1;}// 更新最大边长max_sid = max(max_sid, dp[i][j]);}// 若当前单元格为'0'，则dp[i][j]保持初始值0（无需额外处理）}}// 返回最大正方形的面积（边长的平方）return max_sid * max_sid;}
};

---

3、解题思路

1. 动态规划定义：设dp[i][j]表示以矩阵中第i行第j列元素为右下角的最大正方形的边长。
2. 状态转移方程：如果当前元素matrix[i][j]为 '1'，则dp[i][j]的值取决于其上方、左方和左上方元素的dp值，即dp[i][j] = min(dp[i-1][j], dp[i][j-1], dp[i-1][j-1]) + 1。这是因为要形成一个更大的正方形，这三个方向都必须能形成至少同样大小的正方形。
3. 边界条件：对于第一行或第一列的元素，如果其值为 '1'，则最大正方形边长只能是 1，因为它们无法形成更大的正方形。

4、为什么用动态规划?

要找到最大正方形，本质上需要判断矩阵中每个位置能形成多大的正方形。例如：

• 要判断 (i,j) 能否形成 3x3 的正方形，必须先知道它上方 (i-1,j)、左侧 (i,j-1)、左上方 (i-1,j-1) 能否形成至少 2x2 的正方形。
• 这些子问题（判断 2x2 正方形）会被多次用到（例如右侧、下方的位置可能也需要判断）。

如果用暴力法，这些子问题会被重复计算；而动态规划可以存储子问题的解，避免重复计算。