【最短路问题转换/拓扑排序+dp】P1807 最长路
题目
P1807 最长路

分析
两种做法:
-
将“最长路问题”转化“最短路问题”,在存入边长的时候存相反数即可,最后得到的结果再取相反数就得到了最长路径。时间复杂度为O(n*m)。
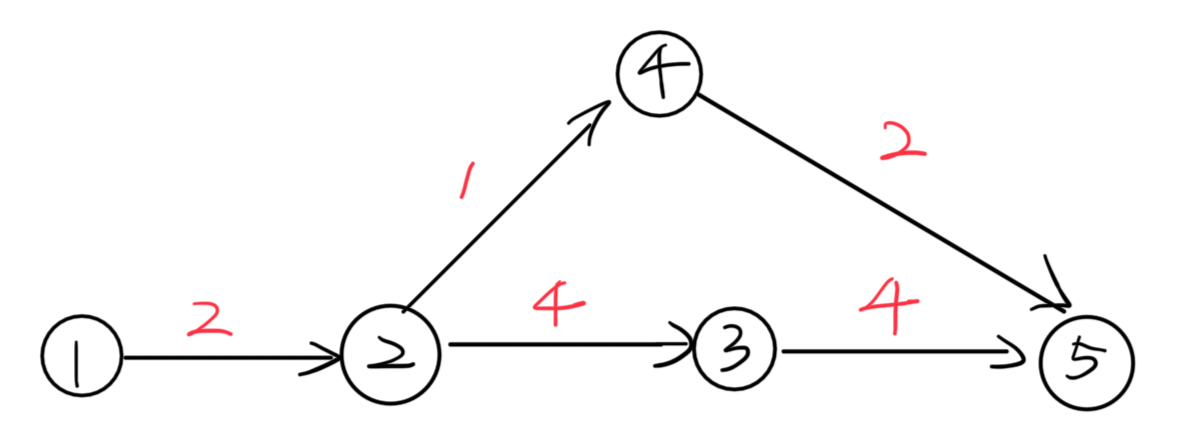
如何让最短路算法选择路径较长的1->2->3->5这条路呢?我们可以将边权存成对应的相反数,那么本身越大的路径就变得越小了,按照最短路算法选择目前最短的路径,再取相反数就是我们原本要求的最长路径。因为涉及负数路径,所以我们只能使用bf或者spfa。 -
由于本题要求的是1号结点到第n号结点之间的最长路径,而结点总个数就是1~n个,所以1号结点的入度为0,n号结点的出度为0,正好可以用拓扑排序按照1号结点到n号结点的方向对路径进行研究,不断取最大值,这就是dp的过程。时间复杂度为O(n+m)。
细节问题:
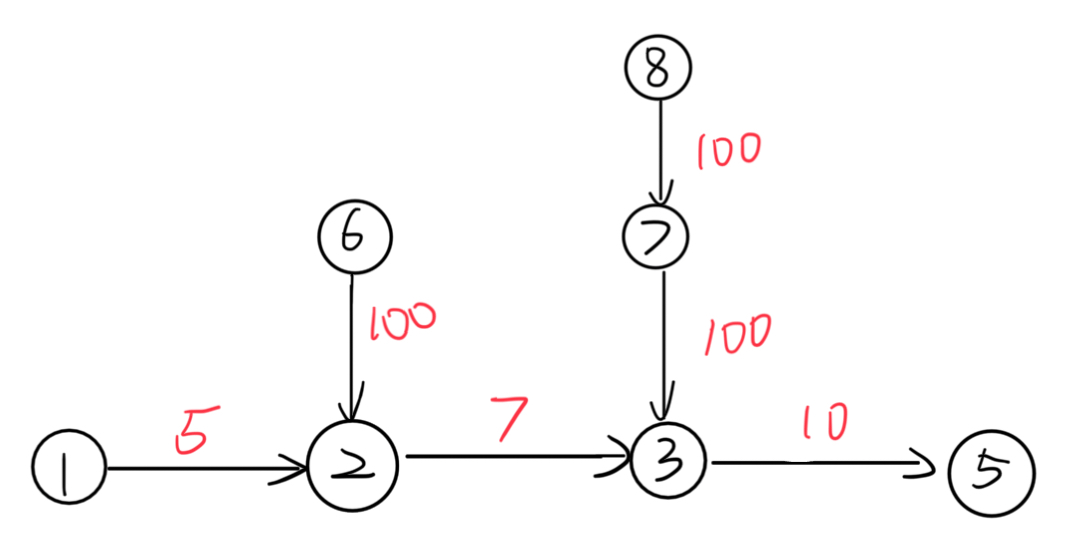
我们要求的是从1到n的最长路,而实际在求最长路的时候,其他入度为0的结点会影响从1到n的结果。所以我们先对除1以外的所有入度为0的结点做一次拓扑排序,将这些可能干扰结果的路线全部砍掉以后,再对1号结点做拓扑排序。
代码
方法1:
//bf算法
#include<iostream>
#include<vector>
#include<cstring>using namespace std;const int N = 1510, INF = 0x3f3f3f3f;typedef pair<int,int> PII;vector<PII> edge[N];int n,m,dist[N],s; //每次找最短边长,经过n-1次更新就可以找到所有点的最短路径
void bf()
{memset(dist,0x3f,sizeof dist); //dist初始化为无穷dist[s] = 0;bool flag = false;//最多执行n-1次,就可以确定所有最短路的边。如果有一次操作没有任何relax,就提前结束 for(int i=1;i<n;i++){flag = false;//对图上每一条边进行relax for(int u=1;u<=n;u++){for(auto& t:edge[u]){int v = t.first, w = t.second;if(dist[u] + w < dist[v]) //s->u->v的距离小于s->v的距离就更新dist[v] {dist[v] = dist[u] + w;flag = true;}}} if(!flag) break; }
}int main()
{cin >> n >> m;s = 1;for(int i=1;i<=m;i++){int u,v,w;cin >> u >> v >> w;edge[u].push_back({v,-w}); //有向边,存相反数 }bf();if(dist[n] == INF) cout << -1 << endl;else cout << -dist[n] << endl;return 0;
}
//spfa
//在bf的基础上用队列优化,将relax过的结点加入队列,并打上标记。直到队列为空结束。
#include<iostream>
#include<vector>
#include<queue>
#include<cstring>using namespace std;typedef pair<int,int> PII;const int N = 1510, INF = 0x3f3f3f3f;vector<PII> edge[N];int n,m,s,dist[N];bool st[N];void spfa()
{memset(dist,0x3f,sizeof dist);dist[s] = 0;queue<int> q;q.push(s);st[s] = true;while(q.size()){int u = q.front(); q.pop();st[u] = false; //出队取消标记!!! for(auto& t:edge[u]){int v = t.first, w = t.second;if(dist[u] + w < dist[v]){dist[v] = dist[u] + w;//因为v发生relax了,把v放入队列并打上标记 if(!st[v]) //一定要检查v是否已经在队列中了!!! {q.push(v);st[v] = true;} }}}
}int main()
{cin >> n >> m;s = 1;for(int i=1;i<=m;i++){int u,v,w; cin >> u >> v >> w;edge[u].push_back({v,-w}); }spfa();if(dist[n] == INF) cout << -1 << endl;else cout << -dist[n] << endl;return 0;
}
方法2:
先看错误代码,没有消除其他入度为0的点的路线
#include<iostream>
#include<vector>
#include<queue>using namespace std;typedef pair<int,int> PII;const int N = 1510;vector<PII> edge[N];int n,m,s,in[N],f[N]; //f[i]:表示从1到i走过的最长路 int main()
{cin >> n >> m;s = 1;for(int i=1;i<=m;i++){int u,v,w; cin >> u >> v >> w;edge[u].push_back({v,w}); in[v]++;}//拓扑排序queue<int> q;//先把所有入度为0的结点加入队列 for(int i=1;i<=n;i++){if(in[i] == 0) q.push(i);f[i] = -1e9;}while(q.size()){int u = q.front(); q.pop();for(auto& t:edge[u]){int v = t.first, w = t.second;in[v]--;f[v] = max(f[v], f[u] + w);if(in[v] == 0) q.push(v);}}if(f[n] == -1e9) cout << -1 << endl;else cout << f[n] << endl;return 0;
}
正确代码:
#include<iostream>
#include<vector>
#include<queue>using namespace std;typedef pair<int,int> PII;const int N = 1510;vector<PII> edge[N];int n,m,s,in[N],f[N]; //f[i]:表示从1到i走过的最长路 int main()
{cin >> n >> m;s = 1;for(int i=1;i<=m;i++){int u,v,w; cin >> u >> v >> w;edge[u].push_back({v,w}); in[v]++;}//拓扑排序queue<int> q;//先把除1外所有入度为0的结点加入队列 for(int i=2;i<=n;i++){if(in[i] == 0) q.push(i);f[i] = -1e9;}while(q.size()){int u = q.front(); q.pop();for(auto& t:edge[u]){int v = t.first;in[v]--;if(in[v] == 0) q.push(v);}}q.push(1);while(q.size()){int u = q.front(); q.pop();for(auto& t:edge[u]){int v = t.first, w = t.second;in[v]--;f[v] = max(f[v], f[u] + w);if(in[v] == 0) q.push(v);}}if(f[n] == -1e9) cout << -1 << endl;else cout << f[n] << endl;return 0;
}
