广度优先遍历-BFS

目录

一、 树的广度优先遍历

1 N 叉树的层序遍历

2 二叉树的锯齿形层序遍历

3 二叉树最大宽度

4 在每个树行中找最大值

二 BFS解决FloodFill问题

1 图像渲染

2 岛屿数量

3 岛屿的最大面积

4 被围绕的区域

三 BFS解决边权为1的单源最短路

1 迷宫中离入口最近的出口

2 最小基因变化

3 单词接龙

4 为高尔夫比赛砍树

四 BFS解决边权为1的多源最短路

1 01 矩阵

2 飞地的数量

3 地图中的最高点

4 地图分析

五 拓扑排序

1 课程表

2 课程表 II

3 火星词典

---

BFS就是宽度优先遍历或者说广度优先遍历，在二叉树或者多叉树或者图中的体现就是从起点开始，一层一层往外遍历，BFS一般都需要借助队列实现。在本章节中，我们首先学习或者说复习一下基础的二叉树的层序遍历，然后再学习BFS解决的FloodFill问题。

一、 树的广度优先遍历

1 N 叉树的层序遍历

429. N 叉树的层序遍历 - 力扣（LeetCode）

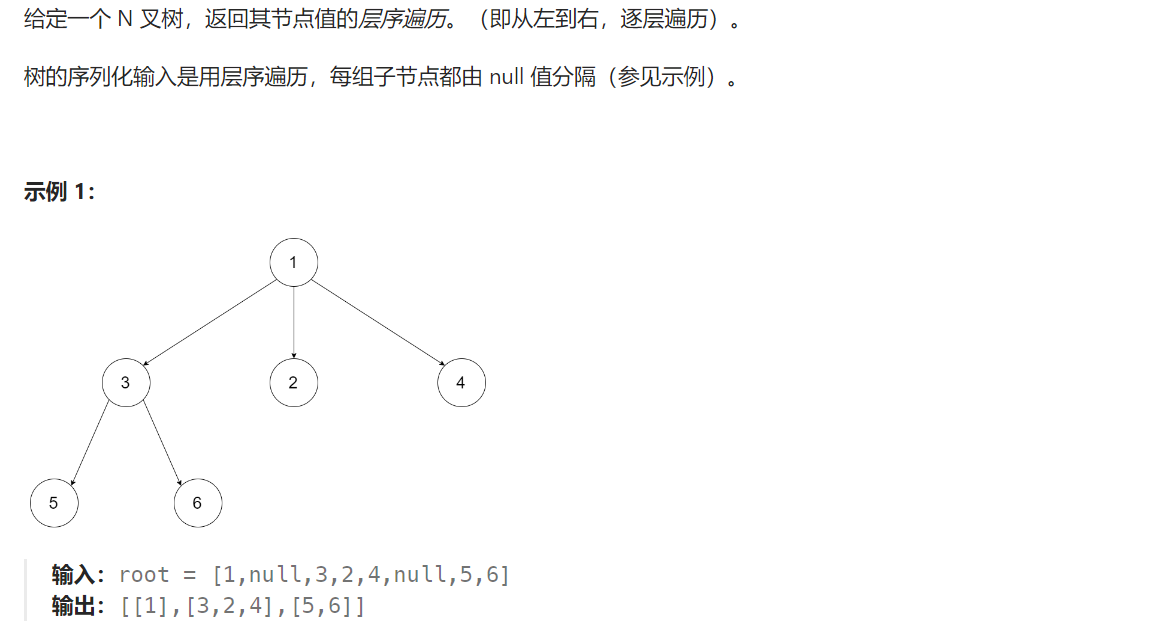
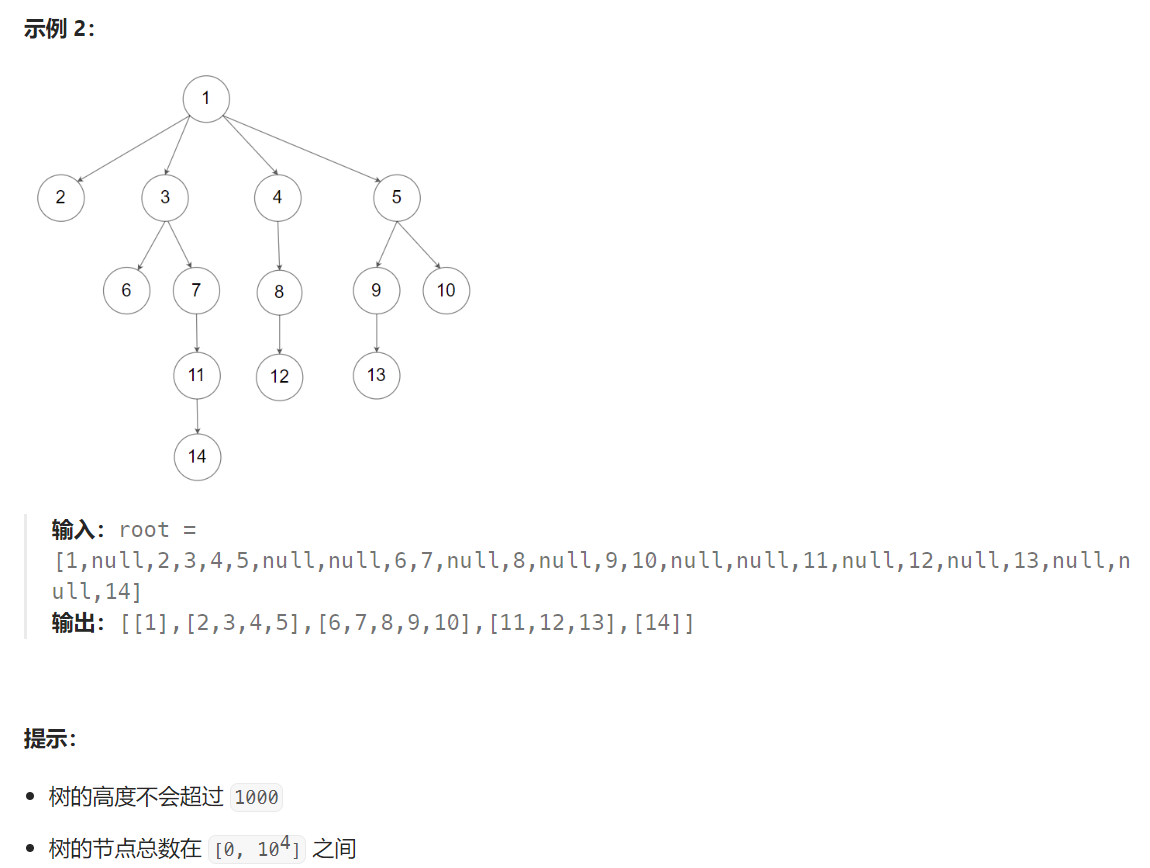
题目解析：题目给定一个N叉树，要求我们返回该N叉树的层序遍历序列，每一层需要从左往右遍历。

这就是一个最基础的BFS，由于是树结构，一定不成环，那么我们不需要对已遍历的节点进行标记防止死循环。

BFS一般步骤：

1、将根节点或者遍历的起点放入队列。 放入队列的节点都是待访问的节点

2、不断从队列取出头部，进行访问，访问完之后，将该节点的子节点加入到队列中。

3、重复以上过程，直到队列为空。

为什么这样能够确保是一层一层访问的呢？因为队列具有先入先出FIFO的特点，我们将节点放入队列的时候就是逐层放入，且从左往右放入的，比如根节点访问的时候，我们是将他的子节点从左往右放入队列中，那么他们出队列也就是访问的顺序也是从左往右的，而没访问完一个子节点，子节点也会将其子节点从左往右放入队列中，这第三层的节点在队列中的位置都是在第二层后面，同时按照从左往右的顺序放入，所以使用队列就能够完成BFS。

我们保存的时候也需要逐层保存，如何逐层保存呢？或者说如何判断本层已经遍历完了呢？首先我们的起点的个数是x ，那么我们首先从队列中取出 x 个节点进行访问，那么访问完这x个结点之后，此时我们拿到了第一层的访问结果，可以放入结果中，而此时队列中的所有节点都是第二层的节点，那么我们就可以继续把这第二层的节点看成起点，保存第二层的节点个数，然后根据节点个数从队列中取出这些节点进行访问，一次类推。

代码如下：

class Solution {
public:vector<vector<int>> levelOrder(Node* root) {vector<vector<int>> res;if(!root) return res;queue<Node*> q;q.push(root);int cnt = 1; //本层节点个数while(!q.empty()){vector<int> tmp;while(cnt--){ //取出本层的节点访问Node* cur = q.front();q.pop();tmp.push_back(cur->val);for(auto& c : cur->children)q.push(c);}cnt = q.size(); //保存下一层的节点个数res.push_back(std::move(tmp));}return res;}
};

2 二叉树的锯齿形层序遍历

103. 二叉树的锯齿形层序遍历 - 力扣（LeetCode）

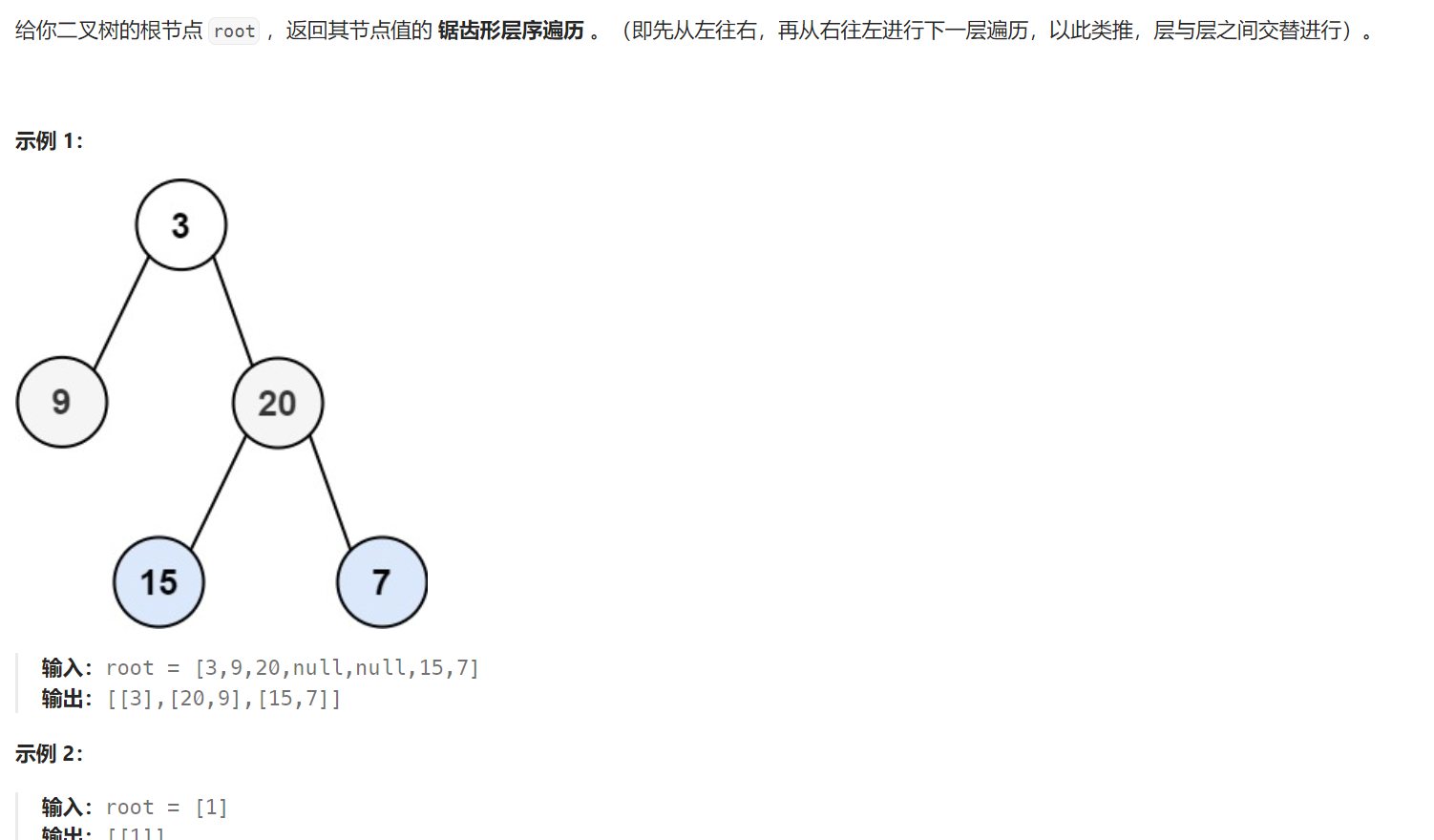
题目解析：本题还是需要逐层对二叉树进行访问，但是是"Z"字形的访问，也就是奇数层（把根节点看成第1层）是从左往右访问，而偶数层是从右往左访问。

本题其实有两种做法，

1、如果我们只追求结果的正确性，而不关注实际访问的顺序，那么可以按照上一题的思路，每一层我们都从左往右访问，但是如果是偶数层，那么先将访问的结果逆置一下再放入结果中。

代码如下：

class Solution {
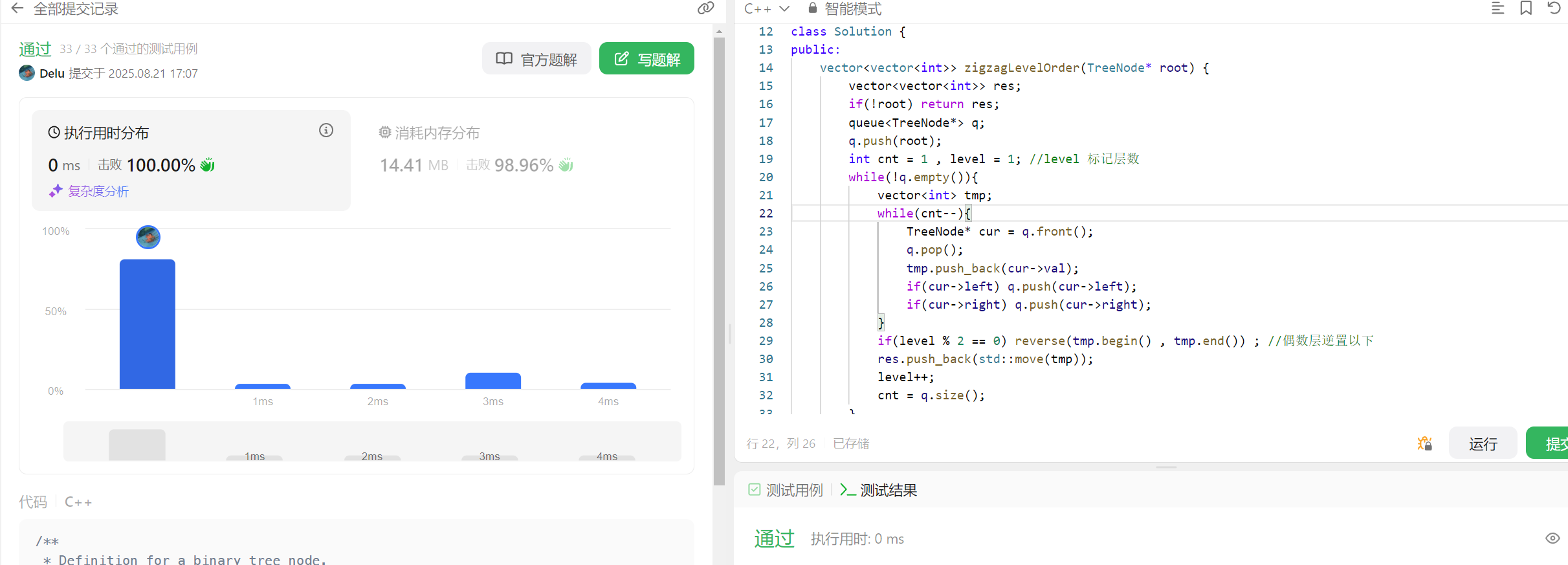
public:vector<vector<int>> zigzagLevelOrder(TreeNode* root) {vector<vector<int>> res;if(!root) return res;queue<TreeNode*> q;q.push(root);int cnt = 1 , level = 1; //level 标记层数while(!q.empty()){vector<int> tmp;while(cnt--){TreeNode* cur = q.front();q.pop();tmp.push_back(cur->val);if(cur->left) q.push(cur->left);if(cur->right) q.push(cur->right);}if(level % 2 == 0) reverse(tmp.begin() , tmp.end()) ; //偶数层逆置以下res.push_back(std::move(tmp));level++;cnt = q.size();}return res;}
};

2、如果我们需要按照"Z"字形的顺序进行层序访问，那么我们可以使用两个栈来实现，因为栈的特点就是后入先出。

我们使用两个栈，st1 用来存储本层访问的节点，st2用来存储下一层访问的节点。

初始情况下st1 = {root} ，访问第一层level = 1，那么访问完之后，将左右孩子按从左到右的顺序放入st2中，那么此时st2={root->left,root->right} ，访问完st1的本层节点之后，我们再 st1.swap(st2)，用st1来访问下一层。

而下一层访问的时候，则是先访问root->right ，如果此时我们还是按照先放左孩子，再放右孩子的顺序，那么st2 = {right->left , right->right , left->left,left->right}，那么下一层的访问顺序就出问题了，所以我们在偶数层的时候，也就是 level % 2 == 0的时候，需要先放右孩子，再放左孩子。

代码如下：

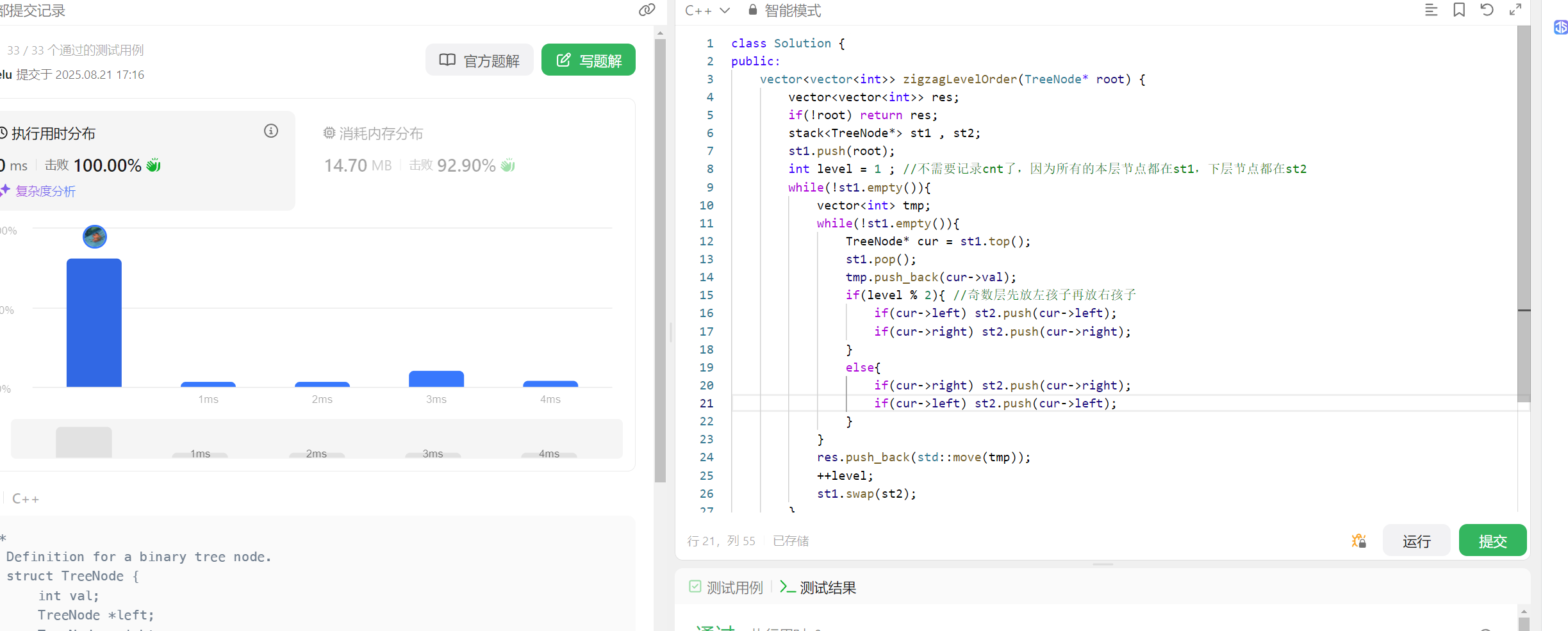
class Solution {
public:vector<vector<int>> zigzagLevelOrder(TreeNode* root) {vector<vector<int>> res;if(!root) return res;stack<TreeNode*> st1 , st2;st1.push(root); int level = 1 ; //不需要记录cnt了，因为所有的本层节点都在st1，下层节点都在st2while(!st1.empty()){vector<int> tmp;while(!st1.empty()){TreeNode* cur = st1.top();st1.pop();tmp.push_back(cur->val);if(level % 2){ //奇数层先放左孩子再放右孩子if(cur->left) st2.push(cur->left);if(cur->right) st2.push(cur->right);}else{if(cur->right) st2.push(cur->right);if(cur->left) st2.push(cur->left);}}res.push_back(std::move(tmp));++level;st1.swap(st2);}return res;}
};

3 二叉树最大宽度

662. 二叉树最大宽度 - 力扣（LeetCode）

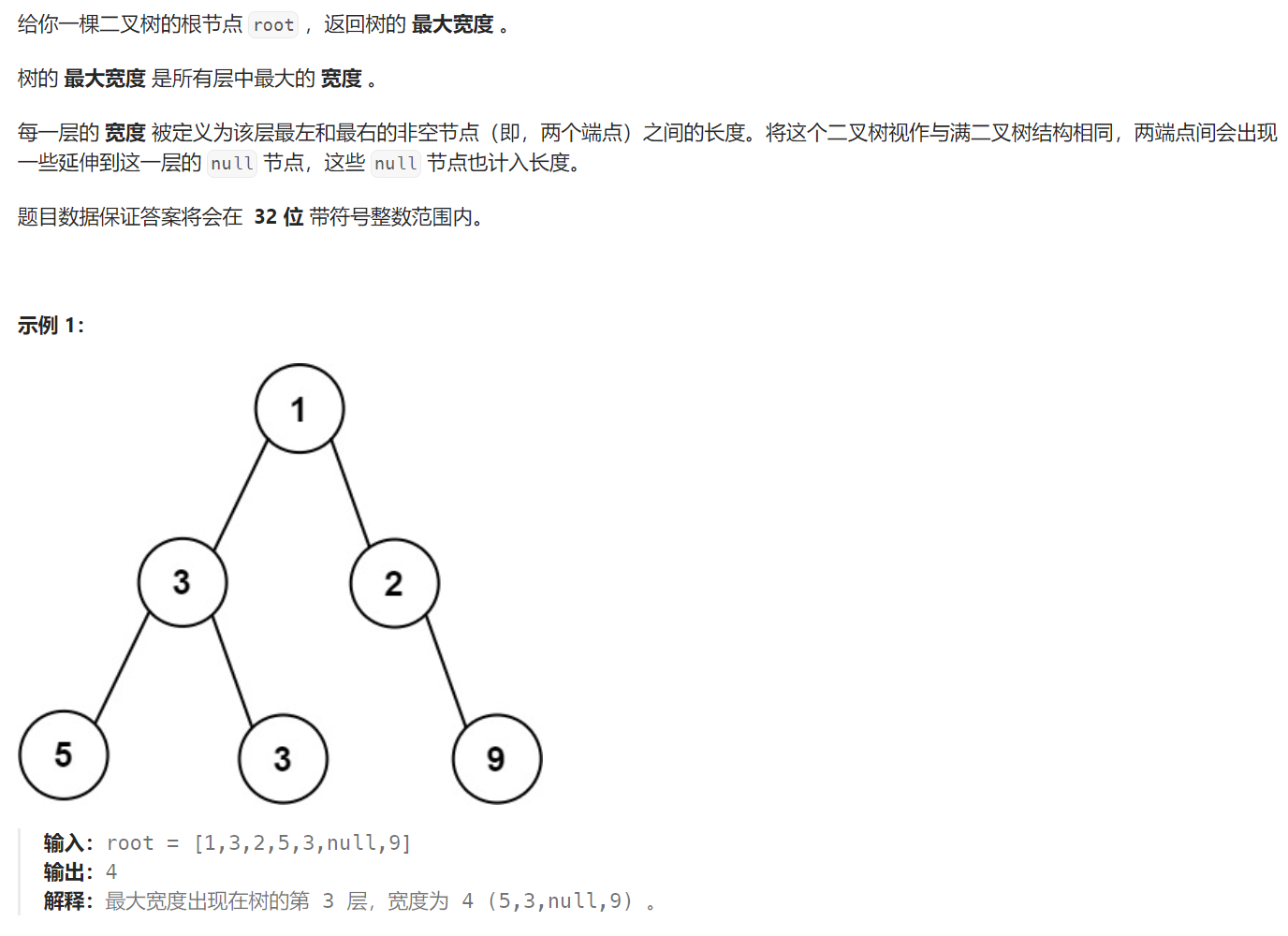
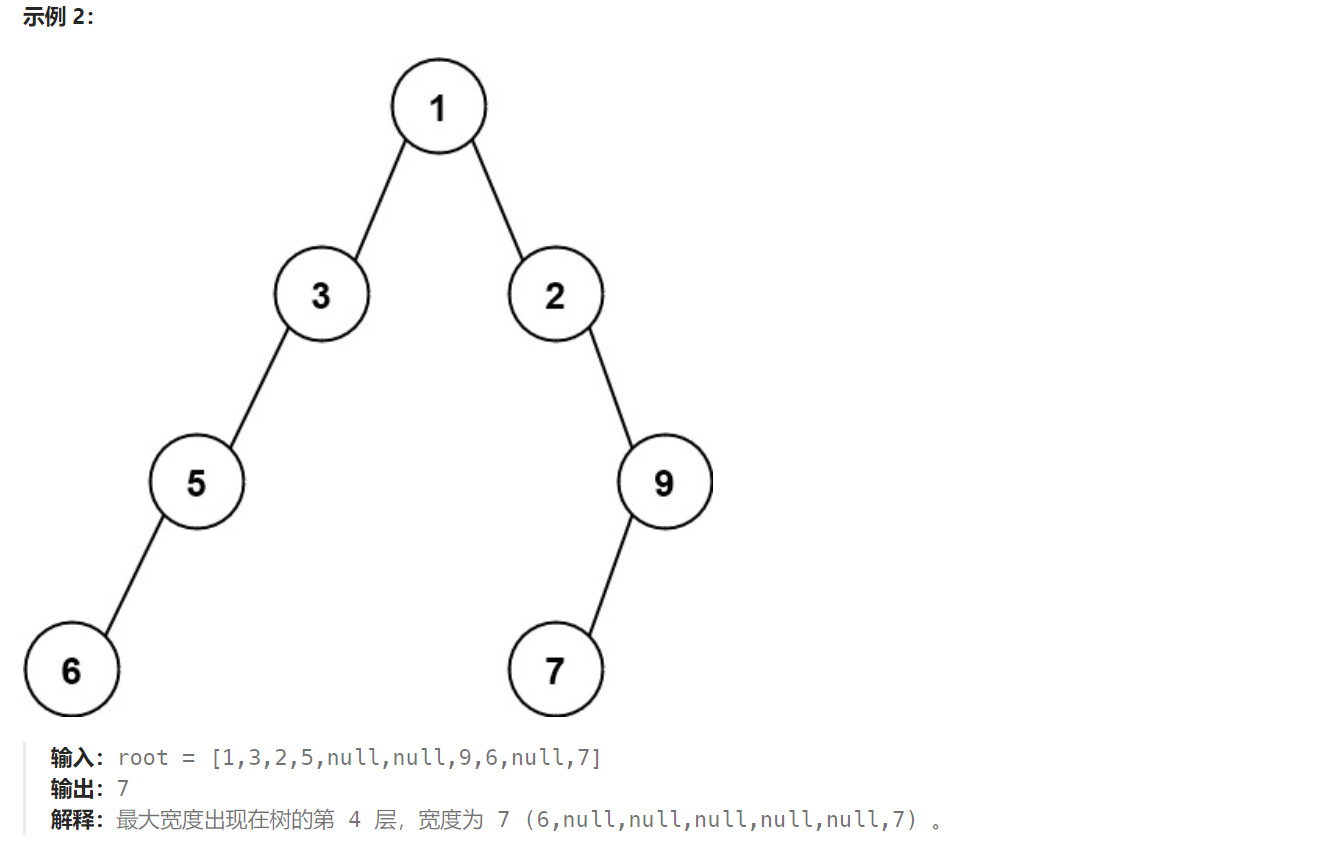
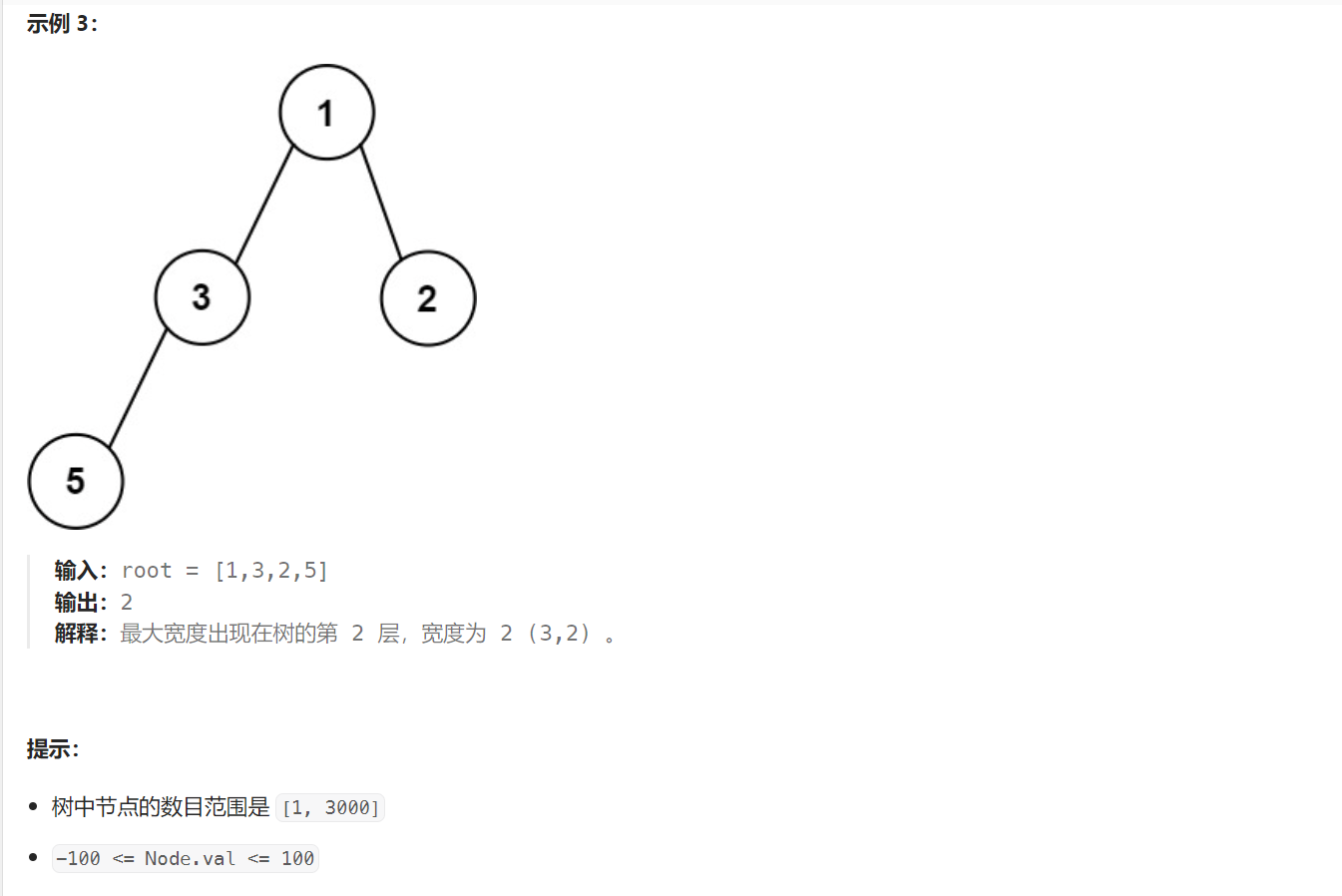
题目解析:本题要求我们求二叉树的最大宽度。而宽度包含本层最左节点和最右解点之间的空节点，我们需要将节点分为空节点和非空节点两类。我们需要将每一层当成完全二叉树的最后一层来看。

这个题具体怎么做呢？ 其实就是当我们访问完节点 cur 之后，即使cur的左右子节点为空，也需要将其放入队列中，标识他的子节点的存在。但是实际在求宽度的时候，并不是所有的空间点都有效，只有最右边的非空节点以及之前的所有非空和空节点才会计入宽度。

解法一：

那么在访问每一层的时候可以这样做： 统计本层已经访问的节点个数cnt，如果当前要访问的节点cur非空，那么说明本层的宽度至少是cnt + 1，我们对保存的最大宽度和 cnt + 1 取一个max ，这样做的好处就是不会遗漏掉最右边的非空节点。

但是这样一来，我们是需要真正的将所有的空节点放入队列，同时会认为空节点也有两个空子节点，全部放入队列中，会导致队列中节点个数过多，比如深度为32的二叉树，光第32层就需要放2^32个节点，我们的内存是绝对不够的。

那么换一种想法，其实我们不关心空节点到底是谁的子节点，而是只关心在两两非空节点之间有多少个空节点，以及在最右非空节点后有多少个空节点，比如：

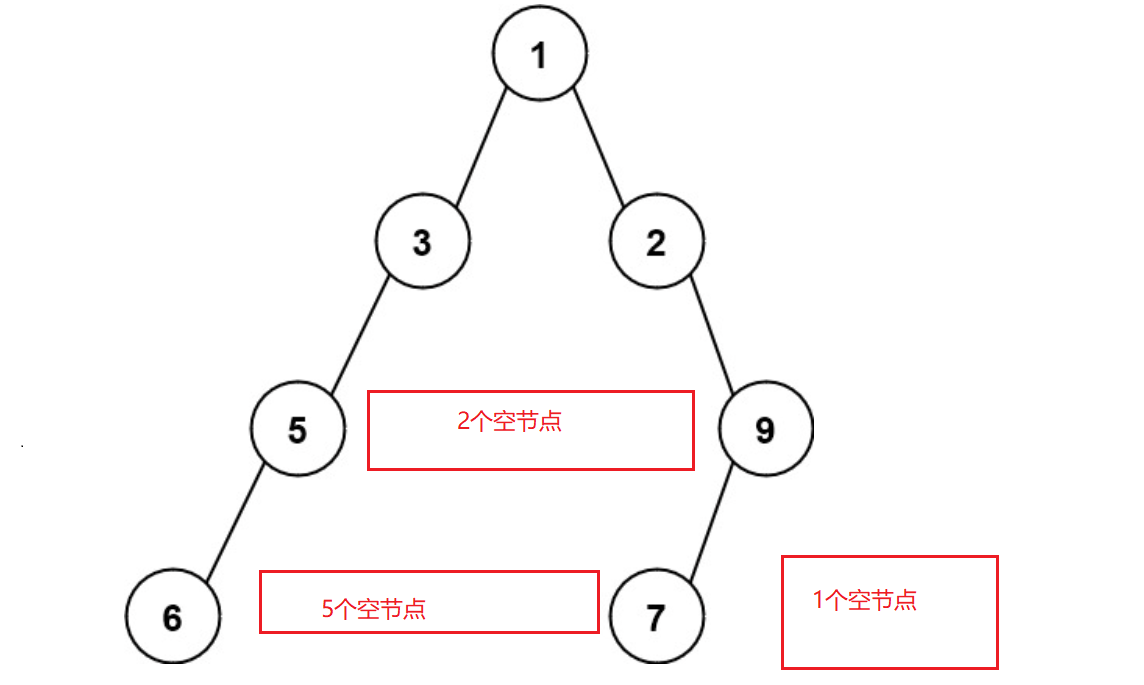
这样一来，我们并不需要真正将空节点一个一个放入队列中，只需要将这一段区间内空节点的个数放入队列中即可。比如上一层的某个区间有 x 个空节点，那么这x个空节点会在下一层延伸出2x个空节点，但是他还需要同前后的空节点区间进行合并。

但是即使这样，最终我们保存的空节点的个数也会很大很大，极端情况下，100层的二叉树，假如只有最左路和最右路的节点，那么中间空节点的个数是十分大的，2^100-2，在long long 都存不下。

不过本题还好，题目明确了最大宽度不会超过int 的范围，所以不会出现这种情况，但是会出现另一种情况，就是100层的情况下，只有最左路节点，在第100层的时候，右边的空节点的个数还是2^100-1，那么还是超出long long 的存储范围。

优化：由于最右边的空节点不影响宽度，他们延伸出来的空子节点也不会影响二叉树的宽度，所以其实最右路的节点并不需要记录，在队列中，只需要记录到最右边的非空节点即可。

那么我们的代码流程可以这样做：当本节点为非空节点时，不管怎么说，此时有一个变量保存在本节点的左孩子之前的连续非空节点个数cnt，如果左子节点为空，那么cnt++，如果右子节点也为空，那么cnt再++，只要没有遇到非空的子节点，都不需要将空节点的数量入队列，而当我们遇到了上一层的连续空节点个数为x，那么cnt+=2*x。

同时，最左侧的空子节点其实也无效，因为只需要统计最左节点个最右节点之间的宽度。

代码如下：

class Solution {
public:typedef pair<TreeNode* , long long> PTL; int widthOfBinaryTree(TreeNode* root) {if(!root) return 0;queue<PTL> q; //保存的pair<TreeNode*,longlong>,如果指针非空，那么数字无意义，如果为空，表示连续空节点的个数q.emplace(root , 0);int res = 1 , count = 1; //count表示本层在队列中的数据个数long long cnt = 0;while(!q.empty()){//取出本层所有节点int w = 0; //记录下一层的宽度,当然也可以用来记录本层的宽度，思路是一样的，不过由于第1层的宽度已经计算过了，我们就从下一层开始记录了             bool flag = false; //标识是否已经遇到最左非空节点while(count--){PTL p = q.front();q.pop();if(p.first == nullptr){cnt += p.second * 2; //将上一层的连续空节点的两个空子节点计算进来// continue;}else{ //说明cur不为空，那么需要判断左右子节点是否为空TreeNode* cur = p.first;if(cur->left == nullptr) cnt++;else{//说明左子节点不为空，那么本段空节点连续区间结束,空节点个数就是cntif(cnt != 0 && flag){ //只有不等于0的时候才需要记录q.emplace(nullptr , cnt);w += cnt; //那么左子节点之前的这段空区间都是宽度的一部分}cnt = 0;w++; //左子节点也是宽度的一部分q.emplace(cur->left,0);flag = true;}if(cur->right == nullptr)cnt++;else{if(cnt != 0 && flag){q.emplace(nullptr , cnt);w += cnt;//右子节点左边的空节点节点区间也是宽度的一部分}w++; //右子节点也需要计算宽度cnt = 0;q.emplace(cur->right,0);flag = true;}//这样一来，最后的一段空子区间，虽然记录了cnt，但是不会计入w，也不会放入队列中，因为只有遇到了非空子节点，才会将该非空节点左边的空区间放入队列中}}count = q.size();res = max(res , w);cnt = 0 ; //注意在这里需要将cnt置为0，否则影响下一层cout<<res<<endl;}return res;}
};

解法二：

上面这种做法写起来十分复杂，同时需要将最多节点的左侧空节点和最右解点的右侧空节点忽略，细节处理十分重要，很容易出错，我们还有一种更简单的做法。

思路： 我们可以将整棵树看成满二叉树，然后为每一个节点编号，假设root编号为0，那么root的左右子节点的编号就是 2*0 + 1  和 2*0 + 2。我们会把子节点的指针和编号放入到队列中，但是不会放空节点。

因为我们每一层的宽度其实可以那最左节点的编号和最右节点的编号进行相减得到，而并不需要关心空节点。

细节：编号的时候，有些节点的编号一定是超出int或者 long long范围的，怎么解决呢？由于题目给定了答案的范围在 int 范围内，不管是最左节点编号超范围还是最右节点编号超出范围，我们的目的都是对两个编号做减法，也就是求两个数的差值，这两个数即使超范围，相减的差值还是正确的。为了支持溢出，我们可以使用unsigned int 来存储编号。

同时由于宽度只与最左节点和最右解点有关，所以在求宽度的时候我们只需要拿出最左非空节点和最右非空节点的编号来求，但是在放子节点的时候需要考虑所有非空节点 。为了支持快速拿出最左和最右节点，我们可以使用vector来模拟队列。

代码如下：

class Solution {
public:typedef pair<TreeNode* , uint32_t> PTS;int widthOfBinaryTree(TreeNode* root) {if(!root) return 0;vector<PTS> q;uint32_t res = 1;q.push_back({root,0});while(!q.empty()){vector<PTS> tmp ; //下一层节点res = max( res , q.back().second - q[0].second + 1) ; //只有一个节点也不会出错for(auto& p : q){if(p.first->left) tmp.push_back({p.first->left , p.second * 2 + 1});if(p.first->right) tmp.push_back({p.first->right , p.second * 2 + 2});}q.swap(tmp);}return res;}
};

这种思路下，不仅代码更简单，时间也更快了，但是要理解这里解决溢出的方案，题目明确了最终结果不会超过int。

4 在每个树行中找最大值

515. 在每个树行中找最大值 - 力扣（LeetCode）

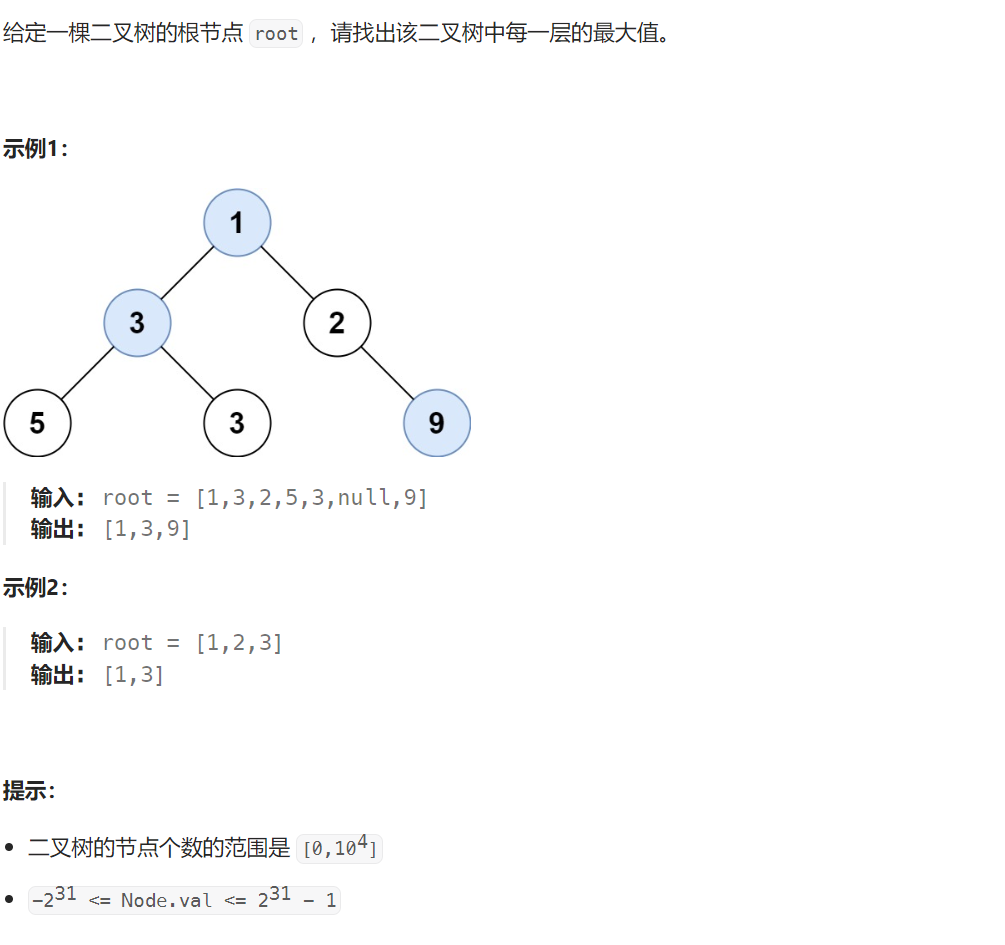
题目解析：题目要求我们求出树的每一层的最大值。

那么就是一个简单的层序遍历，我们按照一层一层遍历，记录最大值就行了。

代码如下：

class Solution {
public:vector<int> largestValues(TreeNode* root) {vector<int> res;if(!root) return res;queue<TreeNode*> q;int cnt = 1;q.push(root);while(q.size()){int m = INT_MIN;while(cnt--){TreeNode* cur = q.front();q.pop();m = max(m , cur->val);if(cur->left) q.push(cur->left);if(cur->right) q.push(cur->right);}res.push_back(m);cnt = q.size();}return res;}
};

二 BFS解决FloodFill问题

FloodFill问题可以理解为洪泛问题，讲一个简单的例子：假设给定一个数组，数组的每一个下标或者二维数组的下标对代表一个位置，而数组存储的值表示该位置的海拔或者说高度，那么在洪水到来的时候，洪水最先淹没的是最低海拔的位置，或者说洪水会流到海拔较低的位置，可以称之为谷，多个联通的谷其实在洪水淹没的时候是一个整体，联通的位置可以称之为连通块，我们在FloodFill问题中，就是要找这些具有相同性质的连通块，求出最大的面积或者其他性质等。而在FloodFill问题中联通的定义有两种：四联通（上下左右）和八联通（在四联通的基础上加上左上右上左下右下），这一类FloodFill问题既可以使用BFS解决，也可以使用DFS解决，这两种搜索算法本质都是一种暴力搜索，枚举所有的情况，判断是否符合条件。

在本章节中的有些题目还会在DFS章节中出现，DFS和BFS可以对照着学习。

1 图像渲染

733. 图像渲染 - 力扣（LeetCode）

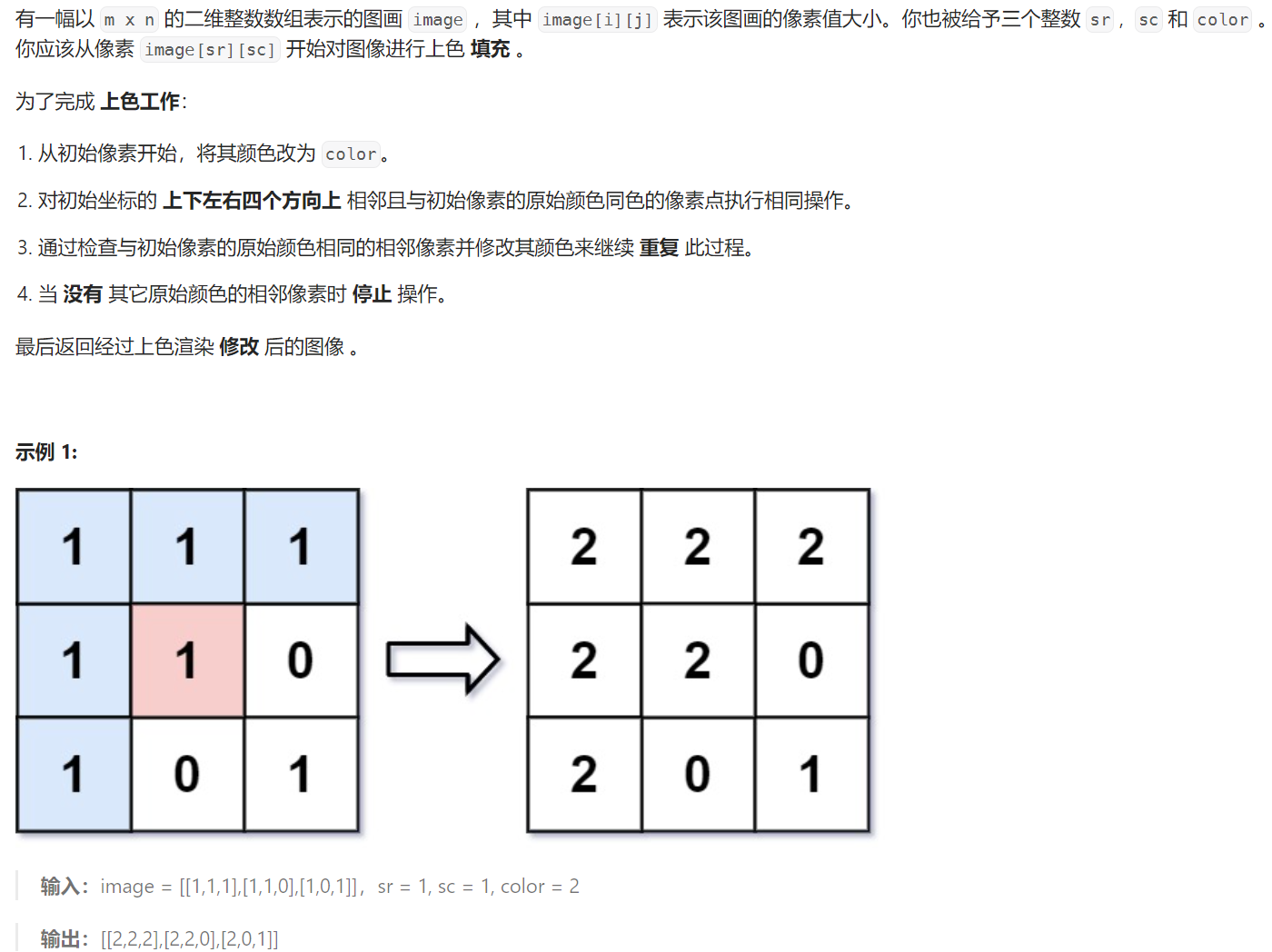
题目解析：题目给定一个颜色数组，给定一个渲染的起点和渲染的颜色，要求我们从起点开始，将与起点相连的与起点颜色相同的像素全部染色为 color。

那么我们可以使用BFS来解决，但是由于图中的联通也就是四/八联通，会导致我们在BFS的时候，将相连位置入队列的时候，比如 (i,j) 将 (i+1,j)入队列了，后续遍历(i+1,j)的时候，可能还会将(i,j)入队列，可能会导致死循环，我们需要确保BFS过程中，每个节点最多访问一次，可以使用一个vector<vector<bool>> vis 数组来标识每个位置是否被访问过。

细节：

1、color可能和起点颜色相同，那么此时与起点原始颜色相同且联通的位置，本身颜色就是color，此时不需要任何处理。 

2、本题由于color与起点颜色相同的情况提前返回了，那么意味着 BFS 的时候 color != mage[sr][sc]，此时有两个小细节：1） 我们什么时候修改颜色呢？是在入队列的时候，还是在出队列的时候，答案是入队列的时候，因为我们入队列的时候修改颜色，后续其他位置再来访问该位置的时候，该位置的颜色就不是起始的颜色了，那么就不会再次入队列，防止重复访问。 2）在本题中。我们是否真的需要一个vis数组来标识呢？本题其实不需要，因为我们在入队列的时候，就已经将颜色修改了，颜色不再是起始颜色，后续也不会再将其入队列了，已经有了标识访问的作用。

同时，我们需要保存起点的原始颜色，用于判断对应位置是否在连通块内，因为起点在入队列的时候颜色就发生改变了，如果不保存，在BFS的循环中无法得知起点颜色。

在求四个相邻位置的下标的时候，由于需要判断下标是否越界，可以直接在代码中暴力求四个下表的值再通过四个if来判断是否合理，但是这样代码过于冗余，我们可以使用一个向量数组的概念，dx=[1,-1,0,0] ， dy = [0,0,1,-1] ，这样一来，我们只需要用一个循环，那么就能根据向量数组的值，来求出四个联通位置的下标，在循环中用if判断是否合法，这样代码的可读性更高。

代码如下：

class Solution {
public:int dx[4] = {0,0,1,-1};int dy[4] = {1,-1,0,0};vector<vector<int>> floodFill(vector<vector<int>>& image, int sr, int sc, int color) {if(image[sr][sc] == color) return image;int m = image.size() , n = image[0].size();queue<pair<int,int>> q;int co = image[sr][sc];image[sr][sc] = color;q.emplace(sr,sc);while(q.size()){auto [row,col] = q.front();q.pop();for(int i = 0 ; i < 4 ; ++i){int x = row + dx[i] , y = col + dy[i]; if(x >= 0 && x < m && y >= 0 && y < n && image[x][y] == co){image[x][y] = color;q.emplace(x,y);}}} return image;}
};

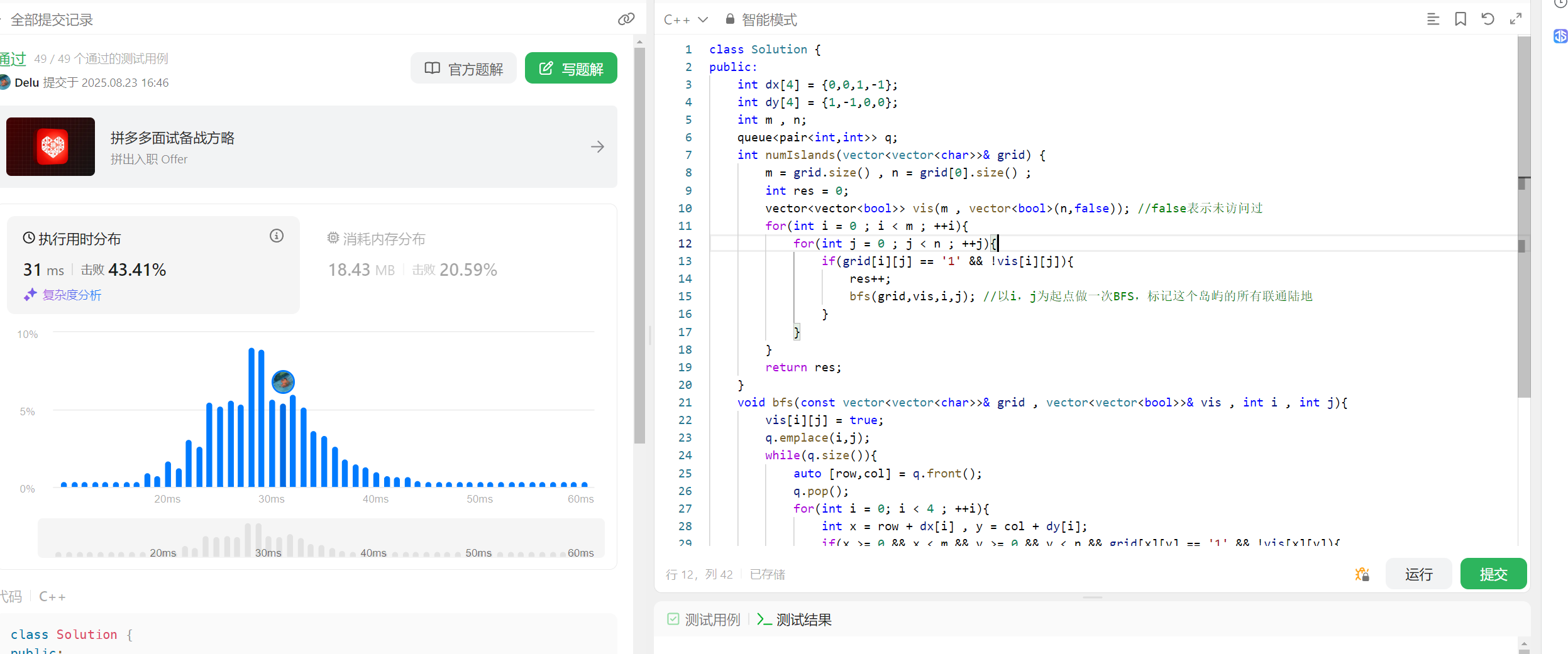
2 岛屿数量

200. 岛屿数量 - 力扣（LeetCode）

题目解析：题目给定一个二维数组，对应位置为1表示是陆地，对应位置为2表示是水，而相连的陆地构成岛屿，让我们求岛屿的数量。

那么我们需要将相连的1看成是一个连通块，每个连通块就是一个岛屿，连通块的数量就是岛屿的数量。那么其实和上一个题类似，只不过本题需要我们自己去找起点，起点也很简单，只要是陆地，同时没有被划分到某个岛屿/没有被访问过的位置，就可以作为起点。

本题如何标记是否被访问呢？两种策略： 1 使用vis数组来标记，这是常规做法，2 将已经访问过的陆地修改为1，后续就不会再次访问该位置了。

观察本题的接口，传进来的参数是外部参数的引用，那么我们最好不好修改外部数据，使用一个vis数组来做最好。

代码如下：

class Solution {
public:int dx[4] = {0,0,1,-1};int dy[4] = {1,-1,0,0};int m , n;queue<pair<int,int>> q; int numIslands(vector<vector<char>>& grid) {m = grid.size() , n = grid[0].size() ;int res = 0;vector<vector<bool>> vis(m , vector<bool>(n,false)); //false表示未访问过for(int i = 0 ; i < m ; ++i){for(int j = 0 ; j < n ; ++j){if(grid[i][j] == '1' && !vis[i][j]){res++;bfs(grid,vis,i,j); //以i，j为起点做一次BFS，标记这个岛屿的所有联通陆地}}}return res;}void bfs(const vector<vector<char>>& grid , vector<vector<bool>>& vis , int i , int j){vis[i][j] = true;q.emplace(i,j);while(q.size()){auto [row,col] = q.front();q.pop();for(int i = 0; i < 4 ; ++i){int x = row + dx[i] , y = col + dy[i];if(x >= 0 && x < m && y >= 0 && y < n && grid[x][y] == '1' && !vis[x][y]){vis[x][y] = true;q.emplace(x,y);}}}}
};

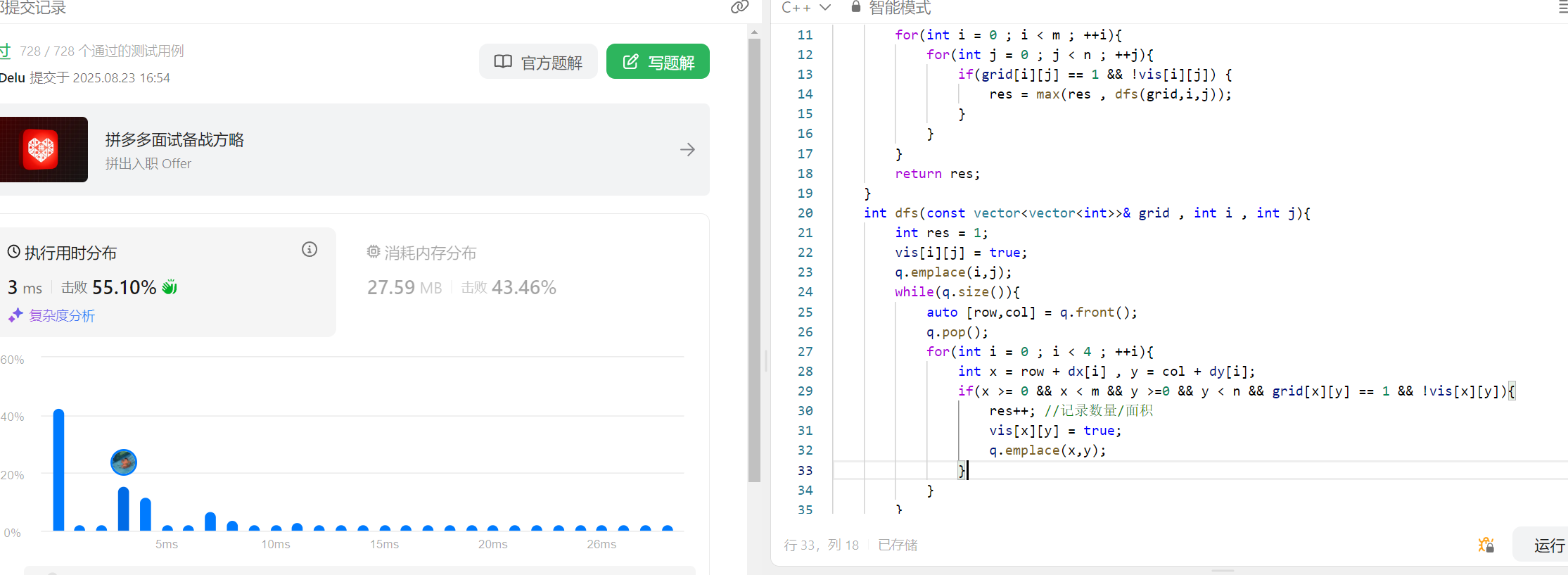
3 岛屿的最大面积

695. 岛屿的最大面积 - 力扣（LeetCode）

题目解析：给定一个数组，数组元素为1表示对应位置是一个陆地，为0表示是海洋，相互连通的陆地构成一个岛屿，要求我们返回最大的岛屿面积。

岛屿面积其实就是联通块的节点个数，这一点我们可以在BFS过程中进行统计，然后记录所有联通块的最大面积就可以了。算法原理和思路与上一个一样。

代码如下：

class Solution {
public:int m , n ;bool vis[50][50] = {false};int dx[4] = {0,0,1,-1};int dy[4] = {1,-1,0,0};queue<pair<int,int>> q;int maxAreaOfIsland(vector<vector<int>>& grid) {m = grid.size() , n = grid[0].size();int res = 0;    for(int i = 0 ; i < m ; ++i){for(int j = 0 ; j < n ; ++j){if(grid[i][j] == 1 && !vis[i][j]) {res = max(res , dfs(grid,i,j));}}}return res;}int dfs(const vector<vector<int>>& grid , int i , int j){int res = 1;vis[i][j] = true;q.emplace(i,j);while(q.size()){auto [row,col] = q.front();q.pop();for(int i = 0 ; i < 4 ; ++i){int x = row + dx[i] , y = col + dy[i];if(x >= 0 && x < m && y >=0 && y < n && grid[x][y] == 1 && !vis[x][y]){res++; //记录数量/面积vis[x][y] = true;q.emplace(x,y);}}}return res;}
};

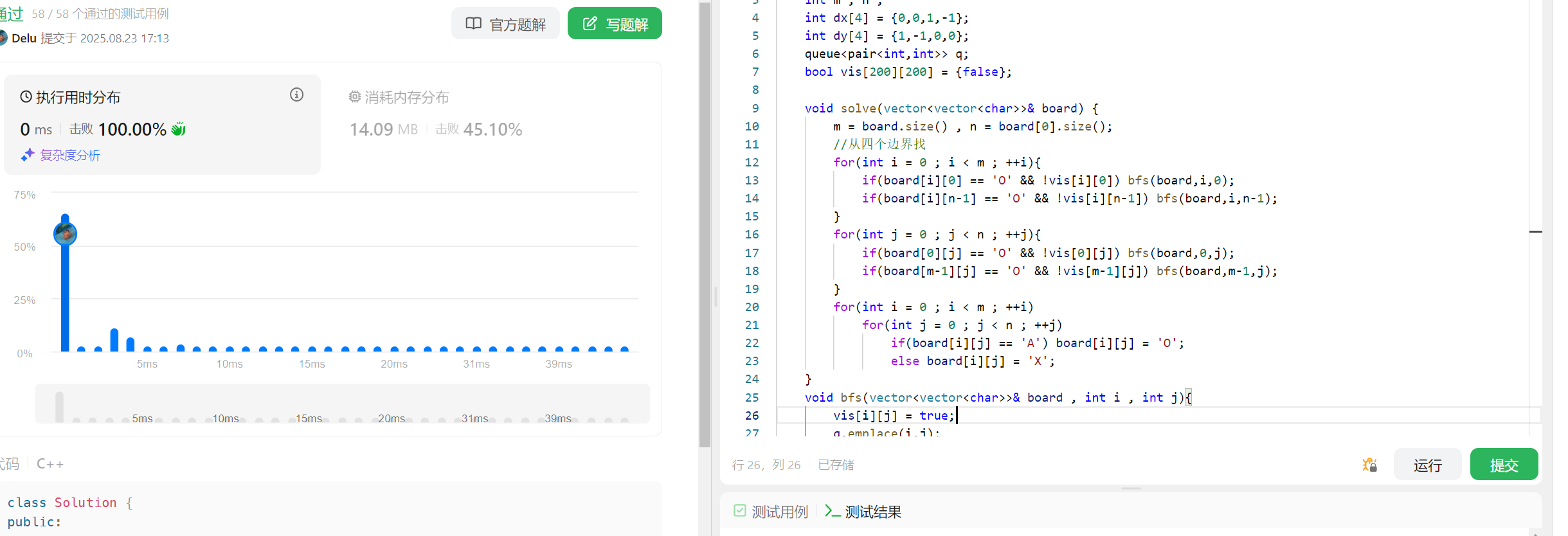
4 被围绕的区域

130. 被围绕的区域 - 力扣（LeetCode）

题目解析：本题要求我们将所有被X完全围绕的O修改为X。

对于一个 O 的联通块，我们如何判断他是否完全为 X 所围绕，而没有任何一个位置处于边界呢？

直接的做法就是遍历数组，从为O的起点出发进行BFS，将途径的O先变为X，如果发现能够连通块有边界位置，那么需要回退，同时需要标记本联通块的位置，后续的BFS不需要重复遍历这些问题。

但是BFS的时候，进行数据的恢复是很复杂的，因为我们在展开BFS的时候就已经将数据变成X了，此时有一种做法就是： 展开的时候，先不变成X，而是修改为其他字符，而后如果BFS展开完了，都没有边界的位置，那么再次以该起点进行BFS，全部修改为X，如果有边界位置，那么就先保持为其他字符，最后返回之前将其他字符修改为O就行了。 但是这样做的话，会进行两次BFS，同时BFS接口设计的时候，还需要传入 原始数据(连通块的数据) 和 修改数据，这样会复杂很多。

我们换一种思路：找没有被完全围绕的 O 的连通块，标记为 其他字符比如 A，最后返回之前，遍历一遍board，如果是 A ，那么修改为 O， 否则全部修改为X。

那么这种思路下，我们只需要在四个边界下找BFS的起点就行了，而且只有一种BFS，从将连通块的O修改为A，接口也较为简单。

代码如下：

class Solution {
public:int m , n ; int dx[4] = {0,0,1,-1};int dy[4] = {1,-1,0,0};queue<pair<int,int>> q;bool vis[200][200] = {false};void solve(vector<vector<char>>& board) {m = board.size() , n = board[0].size();//从四个边界找for(int i = 0 ; i < m ; ++i){if(board[i][0] == 'O' && !vis[i][0]) bfs(board,i,0);if(board[i][n-1] == 'O' && !vis[i][n-1]) bfs(board,i,n-1);}for(int j = 0 ; j < n ; ++j){if(board[0][j] == 'O' && !vis[0][j]) bfs(board,0,j);if(board[m-1][j] == 'O' && !vis[m-1][j]) bfs(board,m-1,j);}for(int i = 0 ; i < m ; ++i)for(int j = 0 ; j < n ; ++j)if(board[i][j] == 'A') board[i][j] = 'O';else board[i][j] = 'X';}void bfs(vector<vector<char>>& board , int i , int j){vis[i][j] = true;q.emplace(i,j);board[i][j] = 'A';while(q.size()){auto [row,col] = q.front();q.pop();for(int i = 0 ; i < 4 ; ++i){int x = row + dx[i] , y = col + dy[i];if(x >= 0 && x < m && y >= 0 && y < n && board[x][y] == 'O' && !vis[x][y]){vis[x][y] = true;q.emplace(x,y);board[x][y] = 'A';}}}}
};

三 BFS解决边权为1的单源最短路

最短路问题还有一类就是权值非负的最短路，我们可以使用Dijkstra算法来解决，详见：

Dijkstra算法——不带负权的单源最短路径_disjka路径算法示意图-CSDN博客

1 迷宫中离入口最近的出口

1926. 迷宫中离入口最近的出口 - 力扣（LeetCode）

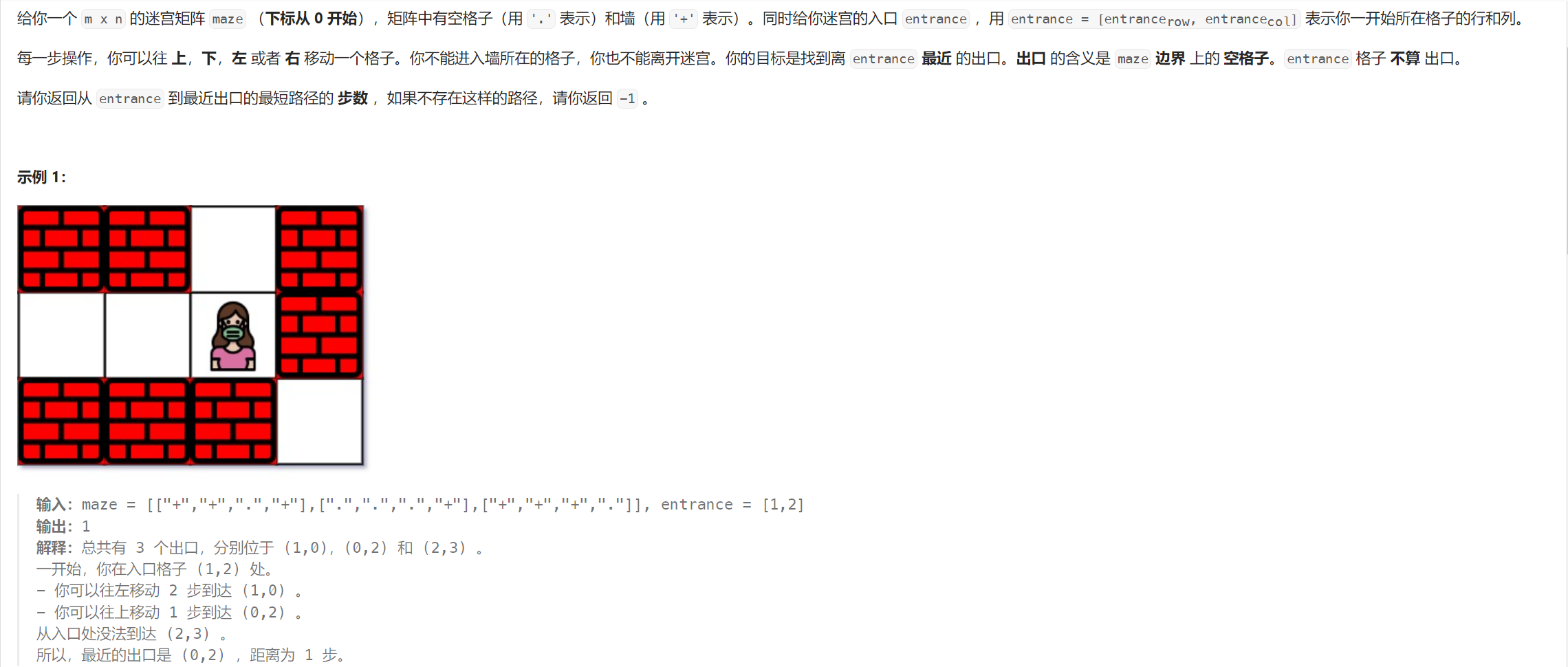
题目解析：题目给定一个二维数组，其中有墙，也有空位，给定一个起点，我们需要从起点走到某一个边界上的空位，就算走到了终点。

本题就是一个简单的单源最短路问题，同时我们可以认为边权为1，因为每一次移动都只需要一步的代价，其实边权为1并不是指权值只能是1，也可以是其他的值，但是要求所有边权相等。

在使用BFS解决单源最短路的时候，我们需要一个dis数组来记录从起点到每一个位置的最小步数，那么是否还需要一个vis数组呢？ 其实不需要了，本题我们可以将所有位置初始化为INT_MAX，那么后续在某一个位置进行移动的时候，如果对应位置当前记录的最短距离比从本位置到该位置这条路线的总距离要短，那么我们就不需要再去更新对应位置，因为有其他的更短路能够到达。

代码如下：

class Solution {
public:int m , n ;int dx[4] = {0,0,1,-1};int dy[4] = {1,-1,0,0}; int nearestExit(vector<vector<char>>& maze, vector<int>& entrance) {m = maze.size() , n = maze[0].size();vector<vector<int>> dis(m,vector<int>(n,INT_MAX));queue<pair<int,int>> q; dis[entrance[0]][entrance[1]] = 0; //起点所需步数为0q.emplace(entrance[0],entrance[1]);//开始bfswhile(q.size()){auto [row , col] = q.front();q.pop();int d = dis[row][col]; //在BFS中，由于权值为1，所以每个节点只进一次队列，是某条最短路的距离cout<<"("<<row<< ","<<col<<")"<<" : "<<d<<endl;if((row == 0 || col == 0 || row == m-1 || col == n-1) && !(row == entrance[0] && col == entrance[1])) return d; //说明这是其中一条最短路的终点，我们直接返回就行了,注意起点不能作为终点for(int i = 0 ; i < 4 ; ++i){int x = row + dx[i] , y = col + dy[i];if(x >= 0 && x < m && y >= 0 && y < n && maze[x][y] == '.' && d + 1 < dis[x][y]){dis[x][y] = d + 1; //不存在说前面记录了一次 dis[x][y]，后续再更新，因为BFS是一层一层往外的，后续更新的d+1一定大于等于当前的d+1q.emplace(x,y);}}}  return -1; //如果前面都没有返回，那么说明走不到}
};

2 最小基因变化

433. 最小基因变化 - 力扣（LeetCode）

题目解析：基因序列就是由八种字符组成的字符串，给定一个start和end，要求我们求出从start变成end所需的最小变化次数。 注意一次只能变化一个字符，同时变化的字符只能在ACGT中选，同时，并不是任意改变都有效，只有改变之后的字符串在基因库中出现，才能进行这种修改。

本质上其实就是一个最短路问题，每一次变化就是一条边，一次变化只能修改一个字符，权值就是1。 但是本题新增了一个基因库，也就是规定了在路径中的节点的字符串只能是哪一些，为了快速判断是否为与基因库，我们可以将基因库的字符串用一个哈希表存储起来。

同时，由于节点存储的值变成了string，那么我们无法再使用dis数组来记录了，而是需要使用哈希表来充当dis数组。

除去这些之外，就是一个基础的BFS的思路，代码如下：

class Solution {unordered_set<string> valid; //基因库中的有效字符unordered_set<string> vis; //是否找到最短距离，标识是否访问string P = "ACGT"; //可以修改的字符queue<pair<string,int>> q; //也可以存储 pair<string,int>//也可以使用 unordered_map<string,int>dis来存储距离，而 queue<string> q只存储节点字符串
public:int minMutation(string startGene, string endGene, vector<string>& bank) {if(startGene == endGene) return 0;for(auto&s : bank) valid.insert(s);vis.insert(startGene);q.emplace(startGene , 0);while(q.size()){auto [str , d] = q.front();q.pop();if(str == endGene) return d;//开始修改每一个位置for(int i = 0 ; i < 8 ; ++i){char ch = str[i]; //先记录原始字符for(int j = 0 ; j < 4 ; ++j){ //然后尝试修改str[i] = P[j];if(P[j] != ch && valid.count(str) && !vis.count(str)){ //为有效修改，且没有找到过最短路，同时需要避免str变回str死循环q.emplace(str,d+1);vis.insert(str);}}//恢复str[i] = ch;}}return -1; //说明bank为空或者无法到达}
};

3 单词接龙

127. 单词接龙 - 力扣（LeetCode）

题目解析：本题和上一个题类似，只是可以在26个小写字符中变化，同时也有一个字典，中途的转化需要在字典中。

做法与上一个题类似，代码如下：

class Solution {
public:unordered_set<string> valid;unordered_set<string> vis;queue<pair<string,int>> q;int len;int ladderLength(string beginWord, string endWord, vector<string>& wordList) {if(beginWord == endWord) return 0;for(auto& s : wordList) valid.insert(s);if(!valid.count(endWord)) return 0;q.emplace(beginWord,1);  //要返回的是整个序列的长度，包括beginWordvis.insert(beginWord);len = endWord.size();while(q.size()){auto [str, d] = q.front();q.pop();if(str == endWord) return d;for(int i = 0 ; i < len; ++i){char ch = str[i];for(char c = 'a' ; c <= 'z' ; ++c){str[i] = c;if(c != ch && !vis.count(str) && valid.count(str)){q.emplace(str,d+1);vis.insert(str);}}str[i] = ch;}}return 0;}
};

4 为高尔夫比赛砍树

675. 为高尔夫比赛砍树 - 力扣（LeetCode）

题目解析：给定一个二维数组，0标识无法到达的位置，1表示地面，而大于1的值表示树的高度，我们需要按照从低到高的顺序砍树，判断能否砍掉所有的树。

如果我们以(0,0) 为起点，如果只使用一次bfs来求砍完所有树的最短路径的话，那么有些位置可能是需要重复走的，这对于BFS来说，我们怎么看待这些需要重复走的位置呢？如何使用标记数组呢？这样一来会不会陷入左右横跳的死循环呢？ 

所以其实直接一次bfs去找到完整的路径不好做，那么我们是否可以进行拆分呢？虽然这条完整的路径可能会重复走某些位置，但是如果我们拆分成一棵树一棵树的砍：首先从起点走最短路到高度为2的树，这条最短路是不会走重复的路径的，然后从高度为2的树走最短路到高度为3的树，这一条最短路也不会走重复的位置，以此类推，我们能够通过将这条完整的最短路拆分为节点节点之间的最短路，从而便于BFS进行vis数组的标记。

这样一来，我们首先需要找到要砍的所有树，同时每一次bfs都需要清空vis数组。

代码如下：

class Solution {
public:bool vis[50][50] = {false};int dx[4] = {0,0,1,-1};int dy[4] = {1,-1,0,0};int m , n;int cutOffTree(vector<vector<int>>& forest) {m = forest.size() , n = forest[0].size();int res = 0 , maxh = 0;vector<int> tree;for(int i = 0 ; i < m ; ++i){for(int j = 0 ; j < n ; ++j)if(forest[i][j] > 1) tree.push_back(forest[i][j]);}sort(tree.begin(),tree.end());int x = 0 , y = 0;//然后开始分批做最短路for(auto h : tree){ //从第i-1棵树走到第i棵树的bfs// cout<<h<<endl;memset(&vis[0][0] , false ,sizeof vis);vector<int> ret = bfs(x,y,h,forest); //三个参数分别表示起点，以及要找的树的高度if(ret[0] == -1) return -1;res += ret[0];x = ret[1] , y = ret[2]; }return res;}vector<int> bfs(int i , int j , int goal , vector<vector<int>>& forest){if(forest[i][j] == goal) return{0,i,j};queue<vector<int>> q; //保存[row,col,dis]q.push({i,j,0});while(q.size()){auto& v = q.front();int row = v[0] , col = v[1] , d = v[2];q.pop();// if(forest[row][col] == goal){  //返回放在这里会超时//     while(q.size()) q.pop();//     forest[row][col] = 1; //砍掉//     return {d , row , col};// }for(int i = 0 ; i < 4 ; ++i){int x = row + dx[i] , y = col + dy[i];if(x >= 0 && x < m && y >= 0 && y < n && !vis[x][y] && forest[x][y] >= 1){if(forest[x][y] == goal){   //将返回提前，减少访问次数forest[x][y] = 1;return {d+1,x,y};}vis[x][y] = true;q.push({x,y,d+1});}}}return {-1,0,0};}
};

四 BFS解决边权为1的多源最短路

多源最短路和单源最短路区别就在于起点的个数，多源最短路是求从多个起点到目标终点的最短路径。 我们当然可以将多源最短路拆成多个单源最短路，去所有起点出发的最短路的最小值，但是这样一来需要做多个BFS，同时在每个BFS中，可能会出现，比如在第一个起点求最短路时，我们已经知道从到(x,y)的最短距离为 d ， 而后续其他节点BFS的时候，该节点到(x,y)的最短距离为d1 > d，但是由于d1是该起点到(x,y)的最短路，所以可能还会从(x,y)去找终点，但是从上帝视角来看，当d1>d的时候，我们就已经没必要再从(x,y)找到终点的最短路了，因为她一定比之前已经计算过的情况差。

比如下面的：当我们计算过了src3到dst的最短距离之后，后续再去从src1和src2进行BFS，虽然他们也有到达dst的最短路径，但是他们的最短路径中经过了src3，那么他们的最短路径（或者说从src1和src2到src3，再从src3到终点的这条路径）一定是不如src3到终点的最短路径的，这样会导致这两条路径其实做了没有意义的计算。

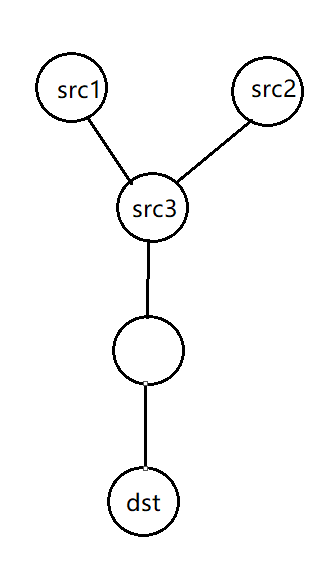
如何解决呢？我们联想一下二叉树的BFS，当根节点访问完之后，我们接下来会访问第2层也就是根节点的左右子节点，那么我们在访问第2层的时候是不是可以看成有两个起点，以两个节点作为起点在做BFS或者说求最短路？甚至第三层的话，我们可以看成有四个起点... ...，那么多源最短路这里也是一样的，我们完全可以在初始化的时候，就将多个起点扔到队列里面来做BFS，后续访问某一个节点的时候，发现他能到达的某个节点已经有了更短的从其他起点到达的路径，那么我们不更新对应的dis就行了。

1 01 矩阵

542. 01 矩阵 - 力扣（LeetCode）

题目解析：本题给定一个二维01矩阵，要求我们求出每一个位置到最近的0的距离。

那么我们以所有的0为起点做一次多源最短路就行了。

代码如下：

class Solution {
public:int m ,n;queue<pair<int,int>> q;int dx[4] = {0 , 0 , 1 , -1}; int dy[4] = {1 , -1 , 0 , 0}; vector<vector<int>> updateMatrix(vector<vector<int>>& mat) {m = mat.size() , n = mat[0].size();vector<vector<int>> dis(m,vector<int>(n,INT_MAX));for(int i = 0 ; i < m ; ++i){for(int j = 0 ; j < n ; ++j){if(mat[i][j] == 0){q.emplace(i,j);dis[i][j] = 0;}}}//开始进行BFSwhile(q.size()){//每一个节点只会进一次队列auto [row,col] = q.front();q.pop();int d = dis[row][col];for(int i = 0 ; i < 4 ; ++i){int x = row + dx[i] , y = col + dy[i];if(x >= 0 && x < m && y >= 0 && y < n && dis[x][y] > d + 1){ //说明(x,y)在之前没有被展开到，那么本次就是最短路dis[x][y] = d + 1;q.emplace(x,y);}}}return dis;}
};

2 飞地的数量

1020. 飞地的数量 - 力扣（LeetCode）

题目解析：

本题其实就类似于上面的 二.4 被围绕的区域 , 求飞地的数量其实就是在求被围绕的区域有多大。

我们还是可以以边界点为起点进行BFS，不过由于可能有多个起点，那么我们可以直接做多源BFS。我们在BFS的过程中，可以把所有不被围绕的陆地修改为0或者2，那么经过BFS之后，剩下的数组中的 1 就是被围绕的飞地。

代码如下：

class Solution {
public:int m , n ;int dx[4] = {0,0,1,-1};int dy[4] = {1,-1,0,0};queue<pair<int,int>> q;int numEnclaves(vector<vector<int>>& grid) {m = grid.size() , n = grid[0].size();//上边界和下边界for(int j = 0 ; j < n ; ++j){if(grid[0][j] == 1){grid[0][j] = 2;q.emplace(0,j);}if(grid[m-1][j] == 1){grid[m-1][j] = 2;q.emplace(m-1,j);}}//左边界和右边界for(int i = 0 ; i < m ; ++i){if(grid[i][0] == 1){grid[i][0] = 2;q.emplace(i,0);}if(grid[i][n-1] == 1){grid[i][n-1] = 2;q.emplace(i,n-1);}}//开始BFSwhile(q.size()){auto [row,col] = q.front();q.pop();for(int i = 0 ; i < 4 ; ++i){int x = row + dx[i] , y = col + dy[i];if(x >= 0 && x < m && y >= 0 && y < n && grid[x][y] == 1){q.emplace(x,y);grid[x][y] = 2;}}}//BFS完之后，所有没有被围绕的1都变成了2，那么剩下的1就是飞地int res = 0 ;for(int i = 0 ; i < m ; ++i){for(int j = 0 ; j < n ; ++j)if(grid[i][j] == 1) res++;}return res;}};

3 地图中的最高点

1765. 地图中的最高点 - 力扣（LeetCode）

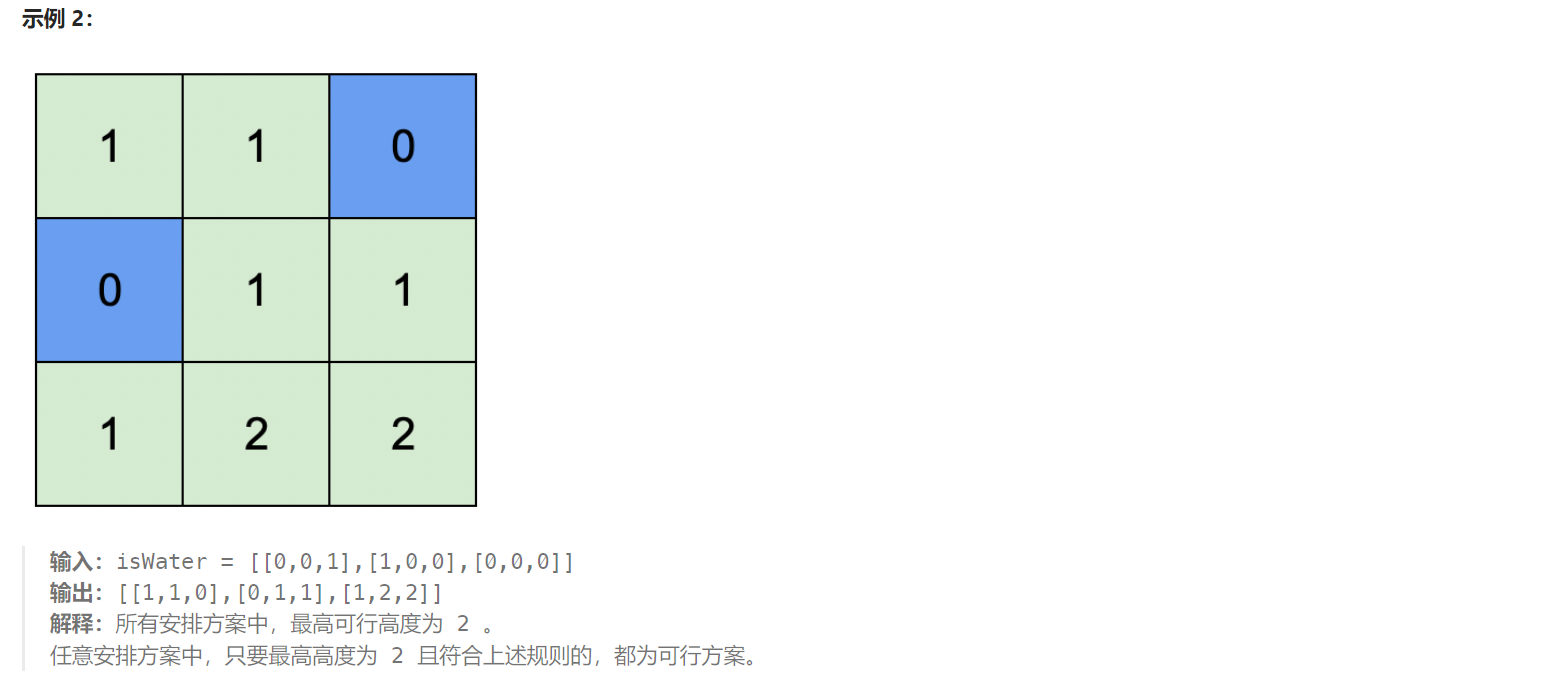
题目解析：题目给定一个二维矩阵，元素为1表示水域，水域的高度为0，元素为0表示陆地，陆地的高度有一定限制，就是任意相邻两块陆地的高度差至多为1，题目要求返回在所有满足条件的方案中，陆地的最大高度。

本题如何思考呢？ 我们以单源最短路的思路来举例，假设只有一块水域，那么水域所有相邻的陆地的高度就是1，这些陆地我们称之为集合 {level1} ，而因为我们要使最高的陆地高度最高，那么其实要使每块陆地都尽可能较高，那么 {level} 中的陆地他们也有相邻的陆地，他们相邻的陆地如果不在{level1}中，那么我们可以让他们的高度为2，这个集合我们称之为 {level2} ，同时{level2}的所有陆地也有相邻的陆地，这些相邻的陆地中，除了{level1} 和 {level2} 中包含的陆地，其他陆地我们将其高度设置为 3 ，依次类推。 我们让与(x,y) 相邻的陆地的高度差要么为-1，要么是0，要么是1，这样其实就类似于树或者图的广度优先遍历， BFS。

那么推广到多源BFS也是一样的，我们以所有的水域为起点进行BFS，那么BFS之后所有相邻的陆地之间的高度差也是-1，0，或者1，也是满足条件的，我们只需要在扩展的时候尽量让相邻未计划陆地的高度比当前陆地高1就行了。 

代码如下：

class Solution {
public:int m , n ;queue<pair<int,int>> q;int dx[4] = {0,0,1,-1};int dy[4] = {1,-1,0,0};vector<vector<int>> highestPeak(vector<vector<int>>& isWater) {m = isWater.size() , n = isWater[0].size();vector<vector<bool>> vis(m,vector<bool>(n,false)); //标识陆地是否已经安排高度/访问for(int i = 0 ; i < m ; ++i){for(int j = 0 ; j < n ; ++j){if(isWater[i][j] == 1){vis[i][j] = true;q.emplace(i,j);}}}//我们使用层序遍历的思路来做，那么最多有多少层，最高的高度就是多少int res = -1; while(q.size()){//本层的高度++res;int cnt = q.size();while(cnt--){auto [row,col] = q.front();isWater[row][col] = res;q.pop();for(int i = 0; i < 4 ; ++i){int x = row + dx[i] , y = col + dy[i];if(x >= 0 && x < m && y >= 0 && y < n && !vis[x][y]){vis[x][y] = true;q.emplace(x,y);}}}}return isWater;}
};

4 地图分析

1162. 地图分析 - 力扣（LeetCode）

题目解析：给定一个二维矩阵，元素为0表示海洋，为1表示陆地，要求我们找出所有海洋中，距离陆地最远的海洋，它距离最近的陆地的曼哈顿距离。

本题其实就是以所有陆地为起点做一次BFS，我们还是可以参考二叉树的层序遍历，一层一层遍历，记录最大层数，就是我们的最大距离。

代码如下：

class Solution {
public:int m , n;queue<pair<int,int>> q;int dx[4] = {0,0,1,-1};int dy[4] = {1,-1,0,0};int maxDistance(vector<vector<int>>& grid) {m = grid.size() , n = grid[0].size();vector<vector<bool>> vis(m,vector<bool>(n,false));for(int i = 0 ; i < m ; ++i){for(int j = 0 ; j < n ; ++j){if(grid[i][j] == 1){vis[i][j] = true;q.emplace(i,j);}}}int dis = -1;while(q.size()){int cnt = q.size();++dis; //本层距离最近陆地的距离while(cnt--){auto [row,col] = q.front();q.pop();for(int i = 0 ; i < 4 ; ++i){int x = row + dx[i] , y = col + dy[i];if(x >= 0 && x < m && y >= 0 && y < n && !vis[x][y]){vis[x][y] = true;q.emplace(x,y);}}}}return dis == 0 ? -1 : dis;  //为0表示全为陆地，为-1表示没有起点也就是全为海洋，这两种情况我们都返回-1}
};

五 拓扑排序

拓扑排序是一种在限定条件下的排序，用于求出解决问题的一个操作步骤序列，比如我们遍历一个无环图，我们需要求出一种遍历顺序，使得以一个点或者多个点为起点能够遍历图中所有点。拓扑排序适用于一下两种场景：

1.有向无环图（DAG图），求出以一个点或者多个点为起点，能够遍历完所有节点的访问顺序，或者说访问序列。

2.定点活动网（AOV网），其中每个节点表示一个活动，而边用来表示活动的先后顺序，边也是有向边，边的起点和终点的关系是： 必须先访问完起点，才能访问终点，但是不要求他们的访问顺序相邻。 拓扑排序可以在AOV网中找到所有活动的一种先后顺序。

图的每个节点都有入度和出度的概念，一个节点的入度就是有多少条边的终点指向该点，而一个节点的出度就是有多少条边从该点出发。

那么不管在DAG图中还是在AOV网中，只有入度为0的点才能够作为起点，因为他们没有前提条件的限制。而入度为0的点可能不止一个，所以拓扑排序的序列也可能不止一个。

我们以AOV网的拓扑排序为例：假设有以下AOV网，每个节点表示一个事件，边表示先后顺序，比如A->D有一条边，表示要做D事件，必须先完成A事件。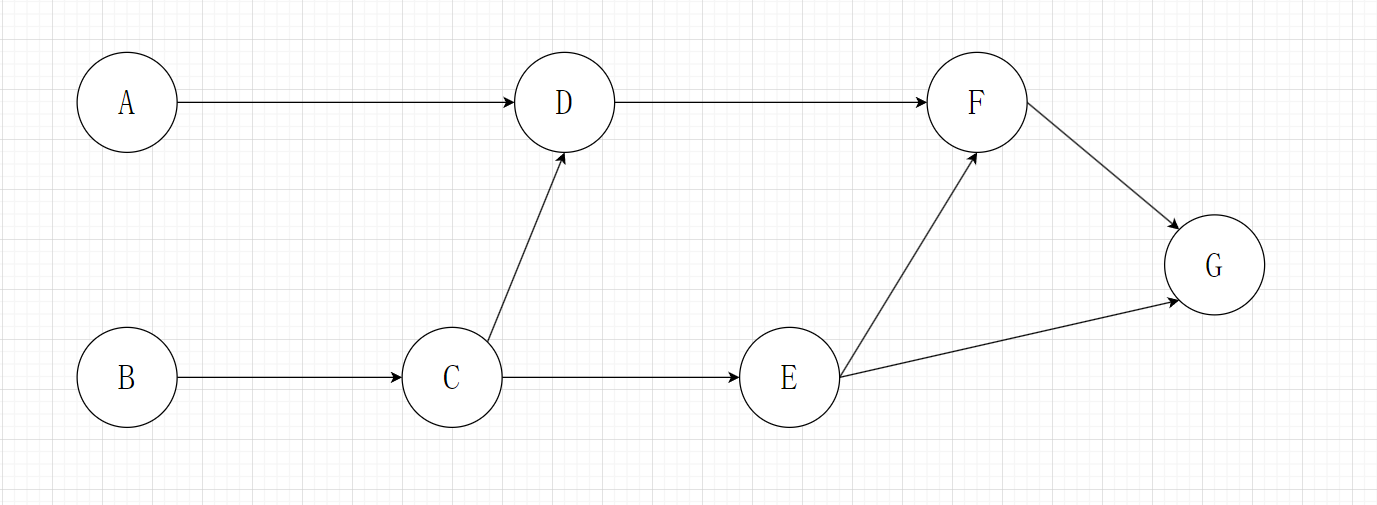

那么我们能够统计出所有节点的入度，degree{A,B,C,D,E,F,G} = {0,0,1,2,1,2,2};那么初始情况下A和B两个入度为0 的事件，这两个事件都可以作为我们的拓扑排序的起点。那么我们假设以B事件为起点，那么完成B事件之后，其实以B为起点的边都需要删除，那么此时AOV网更新，如下图：

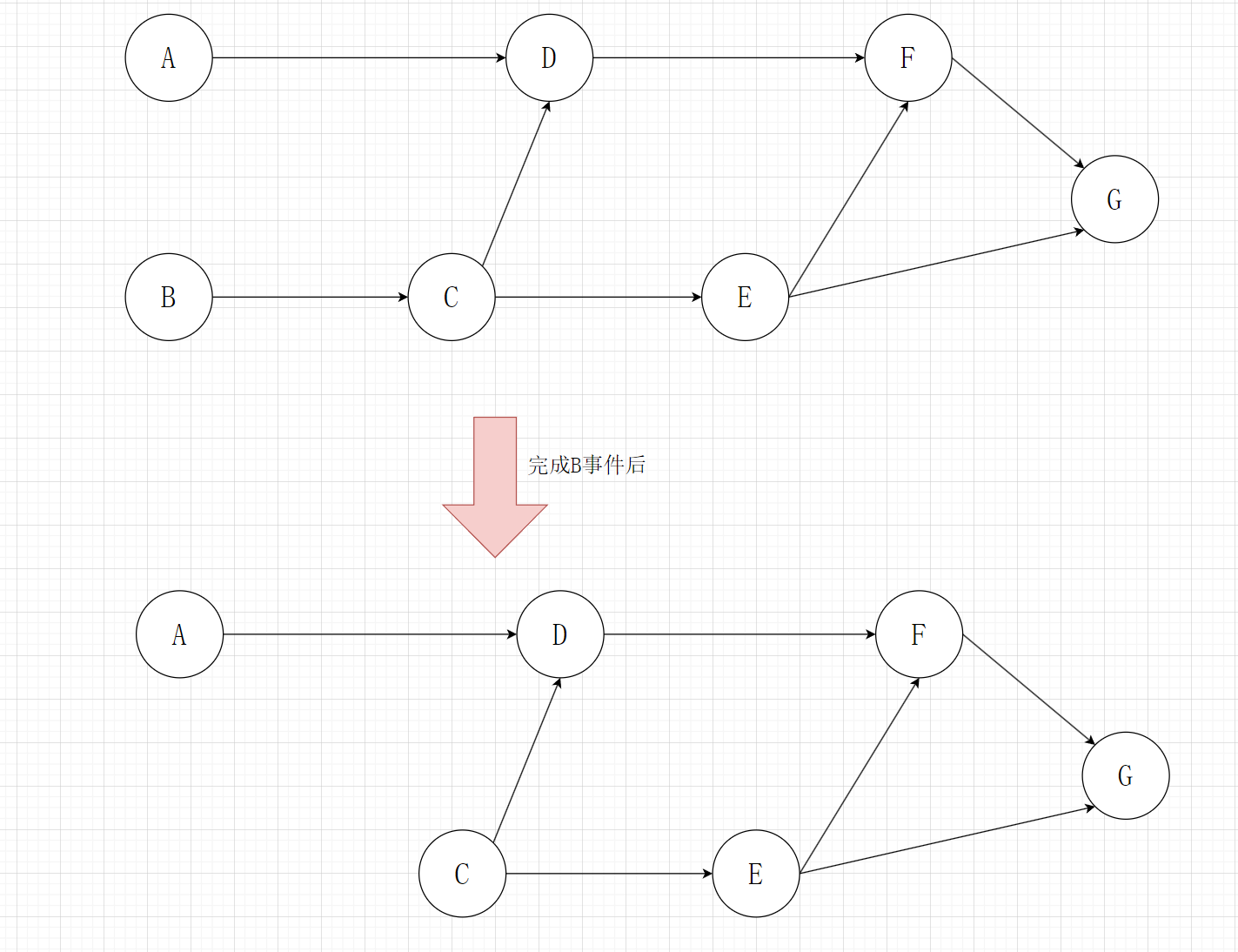
同时，我们在删除B为起点的边的时候，相对应的，这些边的终点的入度需要减一，此时所有节点的入度：  degree{A,C,D,E,F,G} = {0,0,2,1,2,2}，那么此时我们又有两个入度为0的点，可以选择任一个先完成，以此类推，直到完成所有事件。

那么其实拓扑排序的关键或者说步骤就是：

1、选择一个入度为0的点访问或者说入度为0的事件来做

2、删除该点出去的所有边

3、再删除边的时候，需要修改边的终点的入度，如果该终点入度为0了，那么该终点可以直接访问。

4、重复以上过程直到遍历所有点。

那么拓扑排序的代码怎么写呢？首先根据题目给定的点和边，统计所有节点的入度以及一个出边的邻接表，然后我们可以把所有入度为0的点放在队列中等待访问，访问的时候就按照上面的步骤进行就可以了。

拓扑排序还可以用来判断一个图是否有环，如果图中有环，那么我们无法完成图的拓扑排序，一定会卡在环的起点。

1 课程表

207. 课程表 - 力扣（LeetCode）

题目解析：给定本学期所需要学习的课程数numCources，在给定一个先修课程表，在学习prerequisites[i][1]之前，必须先学习prerequisites[i][0]，要求我们判断是否能够完成所有课程的学习。

本题其实就是看能不能求出一个拓扑排序的序列，代码如下：

class Solution {
public:queue<int> q;bool canFinish(int n, vector<vector<int>>& prerequisites) {vector<int> count(n,0); //入度统计vector<vector<int>> g(n); //出边邻接表for(auto& v : prerequisites){count[v[1]] ++; g[v[0]].push_back(v[1]); //表示从v[0]有一条边到v[1]}for(int i = 0 ; i < n; ++i){if(count[i] == 0){q.push(i);}}int cnt = 0; //记录学习了多少门课程(拓扑序列有多少个点)while(q.size()){int x = q.front();q.pop();cnt++;//删除从x出去的边,修改终点入度for(auto t : g[x]){if(--count[t] == 0) q.push(t); //入度减到0就加入队列等待访问}}return cnt == n;}
};

2 课程表 II

210. 课程表 II - 力扣（LeetCode）

题目解析：本题和上一题类似，但是要求我们返回一个拓扑序列，但是本题有一点鸡贼的是prerequisites[i][0]是后修课程，prerequisites[i][1]是先修课程，在统计入度和邻接表的时候要注意。

那么我们只需稍作修改，在访问节点的时候，不用对其进行计数，而是尾插到数组中。

代码如下：

class Solution {
public:queue<int> q;vector<int> findOrder(int n, vector<vector<int>>& prerequisites) {vector<int> count(n); //统计入度vector<vector<int>> g(n); //出边的邻接表for(auto& v : prerequisites){count[v[0]]++;g[v[1]].push_back(v[0]);}for(int i = 0 ; i < n ; ++i){if(count[i] == 0) q.push(i);}vector<int> res;while(q.size()){int x = q.front();q.pop();res.push_back(x);for(auto t : g[x]){if(--count[t] == 0) q.push(t);}}if(res.size() != n) res.clear();  //说明无法完成，那么将数组置空return res;}
};

3 火星词典

LCR 114. 火星词典 - 力扣（LeetCode）

题目解析：题目给定一组按火星语字典序升序排列的字符串，要求我们根据他们的顺序，给出这些字符串中出现过的所有字符的字典序。

比如例1： words = ["wrt", "wrf", "er", "ett", "rftt"] ,那么我们根据words[0] 和 words[1]可以确定 t < f ，根据words[0] 和 words[2]可以确定 w < e ，同时通过words[3] 和 words[4] 可以确定，e < r，根据words[2] 和 words[3]可以确定 r < t ，这样一来，我们其实可以根据大小关系，确定其在字典序的先后顺序，同时我们只需要对出现过的字母进行字典序排序，对于不确定先后顺序的字母我们不需要关心其相对顺序。

我们知道了两两字母之间的大小顺序，那么就可以将其抽象成图，当然其实我们还有一些大小关系没有枚举出来，比如 w < r 如下图：

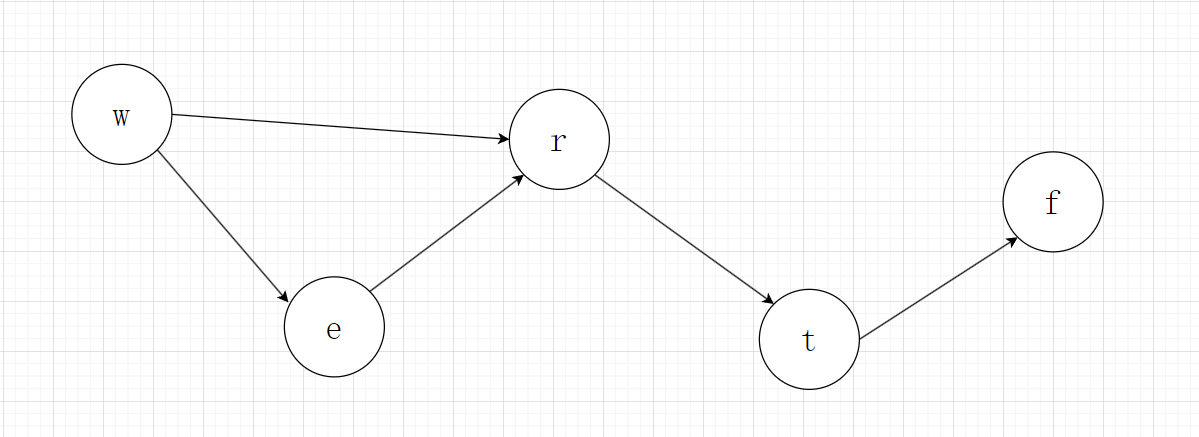
那么我们求出一个这些字符的拓扑排序序列，拓扑序列就是一种字典序。

在统计大小关系的时候,words[i] < words[j] 的时候，那么说明 words[i] 和 words[j]中第一个不相同的字母 words[i][x] < words[j][x] , 但是如果我们发现words[i] 和 words[j] 是这样的情况：words[i] ="abc" ,words[j] = "ab"，那么此时一定无法得出一个拓扑排序。

现在的问题是大小关系一定会有很多重复的，我们是否需要去重？同时还有一些字母可能没出现不需要排序，如何处理？

很简单，我们使用一个 count(26)统计入度，同时使用 flag(26)统计每一个字符是否出现，最后我们还是使用邻接表来统计边vector<vector<int>> ，重复的边我们可以重复统计，因为后续删除的时候会一次性全部删除。

代码如下：

class Solution {
public:queue<int> q;string alienOrder(vector<string>& words) {string res;vector<int> count(26);vector<bool> flag(26,false);vector<vector<int>> g(26); int n = words.size();for(int i = 0 ; i < n ; ++i){for(int j = i + 1 ;j < n ; ++j){//找出 words[i] 和 words[j] 的第一个不同的字符int len = min(words[i].size() , words[j].size());int x = 0; //第一个不同的下标for(; x < len ; ++x){if(words[i][x] != words[j][x]) break;}if(x < len){//说明 words[i][x] < words[j][x]count[words[j][x] - 'a'] ++;g[words[i][x]-'a'].push_back(words[j][x] - 'a');}else if(words[i].size() > words[j].size()) return res; //没有出现不同，类似于 "ab" "abc"}}//统计所有出现的字符int cnt = 0 ;//出现的字符种类数for(auto& s:words){for(auto ch : s){if(!flag[ch - 'a']){cnt++;flag[ch-'a'] = true;}}}//然后进行拓扑排序for(int i = 0 ; i < 26 ; ++i){if(flag[i] && count[i] == 0) q.push(i);}while(q.size()){int x = q.front();q.pop();res += x + 'a';//删除xfor(auto t : g[x]){if(--count[t] == 0) q.push(t);}}return res.size() == cnt ? res : "";}};

总结

BFS算法虽然很简单，但是它的应用却十分广泛，不仅能够在二叉树和多叉树中实现层序遍历，还能够解决边权为1的单源和多源最短路问题，以及拓扑排序的问题，在算法设计和代码设计中，我们要思考如何标记某个节点已经访问或者是否真正需要一个vis数组来进行标记？能否通过我们在BFS过程中使用到的诸如距离，高度等量值，间接判断节点是否访问。