当前位置：首页 > news >正文

最大子数组和【栈和分治两种思路】

news 2025/8/26 14:02:16

示例 1：
输入：nums = [-2,1,-3,4,-1,2,1,-5,4]
输出：6
解释：连续子数组 [4,-1,2,1] 的和最大，为 6 。
示例 2：
输入：nums = [1]
输出：1
其中：
1 <= nums.length <= 105
-10⁴ <= nums[i] <= 10⁴
LeetCode链接：https://leetcode.cn/problems/maximum-subarray/description

方法一：
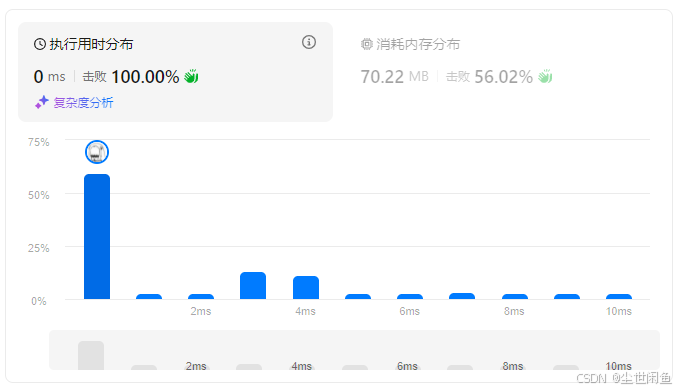
非负栈。该思路参考栈的特点，假设存在一个栈，其中记录的是最大子数组。此时，栈中的元素和存在两种情况：1、元素和非负，此时可以继续向栈中添加元素并判断是否为最大和；2、元素和为负，此时表明后续再添加元素也不会得到最大元素和，此时将栈清空即可。由于并不需要给出最大子数组，因此并不需要构建栈，只需要记录当前元素和即可。
边界情况处理。需要考虑值全小于零的情况，此处可以用注释部分的逻辑解决，也可以使用代码中的最大元素初始值设为INT_MIN，并每次都进行比较解决。
时间复杂度。单层for循环，时间复杂度为O(n)。
空间复杂度。使用了常数个额外空间，时间复杂度为O(1)。

class Solution {
public:int maxSubArray(vector<int>& nums) {int sum = 0, maxSum = INT_MIN;// vector<int> _nums=nums;// sort(_nums.begin(),_nums.end(), greater());// if(_nums[0] <= 0){//     return _nums[0];// }for (int i = 0; i < nums.size(); i++) {// 如果入栈后sum小于0，则清空栈if ((sum + nums[i]) < 0) {sum = 0;maxSum = nums[i] > maxSum ? nums[i] : maxSum;continue;}sum += nums[i];maxSum = sum > maxSum ? sum : maxSum;}return maxSum;}
};

在这里插入图片描述

方法二：
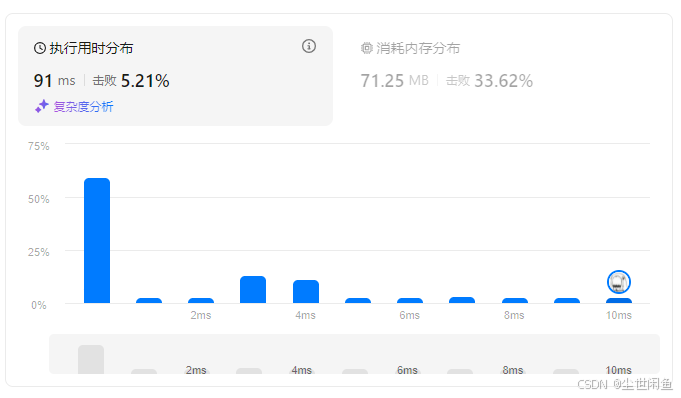
分治法（递归的一种形式）。分治的思想为将问题拆成相同情况，但是不同规模的子问题，并且可以从子问题的解得到原问题的解。对于最大数组和，可以将原始输出分为两部分，则最大数组必定出现在左部分、右部分和跨越左右两部分这三种情况之中。
边界情况处理。需要注意的边界有三点：

在计算M时，直接使用“(L + M)/2”可能会导致正溢出，因此需要使用“L + (R - L) / 2”。
递归时，边界为左闭右闭，因此递归时分别为：(L, M)、(M + 1, R)。
在计算跨越中间的最大值时，循环起始条件应该为：M、M + 1，否则会导致nums[M]被计算两次。

时间复杂度。递归的时间复杂度为O(logn)，对跨越左右的计算为O(n)，因此总体复杂度为O(nlogn)。
空间复杂度。递归栈的空间复杂度一般为O(logn)。

class Solution {
public:int maxSubArray(vector<int>& nums) {return findMax(nums, 0, nums.size() - 1);}int findMax(vector<int>& nums, int L, int R) {if (L == R)return nums[L];int maxL, maxR, maxCross;// 防止大数溢出int M = L + (R - L) / 2;maxL = findMax(nums, L, M);maxR = findMax(nums, M + 1, R);maxCross = crossMax(nums, L, R, M);return max({maxL, maxR, maxCross});}int crossMax(vector<int>& nums, int L, int R, int M) {int maxL = INT_MIN;int sum = 0;for (int i = M; i >= L; i--) {sum = sum + nums[i];maxL = max({sum, maxL});}int maxR = INT_MIN;sum = 0;// 此处要从M+1开始，防止中间节点被计算两次for (int i = M + 1; i <= R; i++) {sum = sum + nums[i];maxR = max({sum, maxR});}return (maxL + maxR);}
};