B样条基函数：从数学原理到Python实现

B样条基函数是计算机图形学、CAD系统和科学计算中的核心数学工具，它通过巧妙的递归结构实现了局部支撑性和可控连续性的完美平衡。本文将深入探讨B样条基函数的数学原理，并提供完整的Python实现。

数学理论基础

B样条基函数 $N_{i,p}(u)$ 由Cox-de Boor递推公式定义，其中 $i$ 表示基函数索引，$p$ 表示阶数，$u$ 为参数变量。

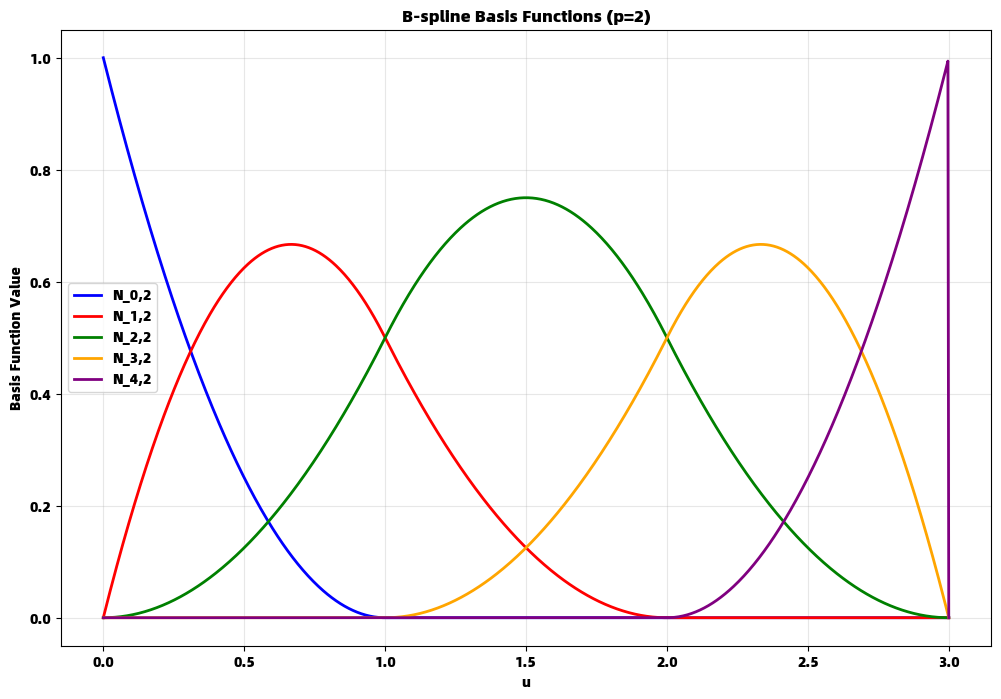
零阶基函数定义

零阶基函数是构建高阶基函数的基础：

$$N_{i,0}(u)=\{\begin{array}{ll}1& \text{若 }{u}_i\le u<u_{i+1}\\ 0& \text{否则}\end{array}$$

高阶递推公式

对于 $p\ge 1$，基函数通过递归方式构建：

$$N_{i,p}(u)=\frac{u-u_i}{u_{i+p}-u_i}{N}_{i,p-1}(u)+\frac{u_{i+p+1}-u}{u_{i+p+1}-u_{i+1}}{N}_{i+1,p-1}(u)$$

这个递推关系确保了基函数具有局部支撑性，每个 $N_{i,p}(u)$ 仅在区间 $[u_i,u_{i+p+1})$ 内非零。

符号推导实现

首先使用Sympy进行符号推导，生成精确的数学表达式：

import sympy as sp
import numpy as np
import matplotlib.pyplot as plt
from sympy import Piecewise, Eq, Andclass BSplineSymbolic:def __init__(self):self.u = sp.symbols('u', real=True)def basis_zero_order(self, i, knots):u_i, u_i1 = knots[i], knots[i+1]if u_i == u_i1:return 0return Piecewise((1, And(u_i <= self.u, self.u < u_i1)),(0, True))def basis_recursive(self, i, p, knots):if p == 0:return self.basis_zero_order(i, knots)u_i, u_i_p = knots[i], knots[i+p]u_i1, u_i_p1 = knots[i+1], knots[i+p+1]denom1 = u_i_p - u_iterm1 = ((self.u - u_i) / denom1 * self.basis_recursive(i, p-1, knots) if denom1 != 0 else 0)denom2 = u_i_p1 - u_i1term2 = ((u_i_p1 - self.u) / denom2 * self.basis_recursive(i+1, p-1, knots) if denom2 != 0 else 0)return term1 + term2def simplify_basis(self, basis_expr):return sp.simplify(basis_expr)def plot_basis_symbolic(self, basis_expr, u_range=(0, 3), points=1000):u_vals = np.linspace(u_range[0], u_range[1], points)f = sp.lambdify(self.u, basis_expr, 'numpy')y_vals = f(u_vals)plt.figure(figsize=(10, 6))plt.plot(u_vals, y_vals, 'b-', linewidth=2)plt.xlabe