[信号与系统个人笔记]第二章 连续时间信号与系统的时域分析

Update

• 2025.8.25
  • 2.1 系统微分方程的经典解

2.1 系统微分方程的经典解

微分方程的基本概念

对于单输入单输出的$LIT$连续系统来说，描述其输入-输出关系 的数学模型是$n$阶常系数线性微分方程，一般形式为：
$$a_n{y}^{(n)}(t)+a_{n-1}{y}^{(n-1)}(t)+\cdots +a_1{y}^{\prime }(t)+a_{0}y(t)=b_m{e}^{(m)}(t)+b_{m-1}{e}^{(m-1)}(t)+\cdots +b_1{e}^{\prime }(t)+b_{0}e(t)$$
$$\sum _{i=0}^n{a}_i{y}^{(i)}(t)=\sum _{j=0}^m{b}_j{e}^{(j)}(t)$$

• 初始条件：$n$阶系统在$t=0$时候接入激励，响应在$t=0_{+}$时刻的值：

  • 初始条件表示激励接入后的瞬间
    $$y^{(j)}(0_{+})(j=0,1,2,\dots ,n-1)$$

• 初始状态：$n$阶系统在激励 没有接入的$t=0$时刻的响应值，该 值反映了系统的历史情况，与激励无关：

  • 初始状态表示激励接入前的瞬间
    $$y^{(j)}(0_{-})(j=0,1,2,\dots ,n-1)$$

微分方程的经典解

齐次解$y_h(t)$

• 微分方程右侧为零时称为齐次方程，即${\sum }_{i=0}^n{a}_i{y}^{(i)}(t)=0$
• 齐次解指齐次方程的解，只由系统的特征根决定

$n$阶微分方程的齐次解

$$y^{(n)}(t)+a_{n-1}{y}^{(n-1)}(t)+\cdots +a_{0}y(t)=0$$
特征方程：
$${\lambda }^n+a_{n-1}+{\lambda }^{n-1}+\cdots +a_1\lambda +a_0=0$$
其中${\lambda }_i$为方程的特征根

• 特征根均为单根：$y_h(t)={\sum }_{i=1}^n{C}_i{e}^{{\lambda }_{i}t}=C_1{e}^{{\lambda }_{1}t}+C_2{e}^{{\lambda }_{2}t}+\cdots +C_n{e}^{{\lambda }_{n}t}$
• 特征根含有$r$重根${\lambda }_i$：$r$重根对应$(C_1{t}^{r-1}+C_2{t}^{r-2}+\cdots +C_{r-1}t+C_r)e^{{\lambda }_{i}t}$
• 特征根 含共轭复根${\lambda }_{1,2}=\alpha \pm j\beta$：共轭复根对应的解为：
  • $e^{\alpha t}[C_1\cos \beta t+C_2\sin \beta t]$
  • $A{e}^{\alpha t}\cos (\beta t-\theta ),A{e}^{j\theta }=C_1+j{C}_2$（辅助角公式）

$n$阶微分方程的特解$y_p(t)$

形如$y^{\prime \prime }+p{y}^{\prime }+qy=e^{\lambda x}{P}_m(x)$：

设特解形如：$y^{\ast }=x^k{e}^{\lambda x}{Q}_m(x)$
其中$Q_m(x)$为一个待定的$m$次多项式
$$k=\{\begin{array}{l}0,\lambda 不是特征根\\ \\ 1,\lambda 是单特征根\\ \\ 2,\lambda 是二重特征根\end{array}$$
将$y^{\ast }$回带原微分方程确定系数即可

形如$y^{\prime \prime }+p{y}^{\prime }+qy=e^{\lambda x}[P_l(x)\cos \omega x+P_n(x)\sin \omega x]$：

设特解形如$y^{\ast }=x^k{e}^{\lambda x}[Q_1(x)\cos \omega x+Q_2(x)\sin \omega x]$
其中$Q_1(x),Q_2(x)$为待定$m$次多项式，m=max{l,n}m=max\{ l,n \}m=max{l,n}
$$k=\{\begin{array}{l}0,\lambda \pm j\omega 不是特征根\\ \\ 1,\lambda \pm j\omega 是特征根\end{array}$$

将$y^{\ast }$回带原微分方程确定系数即可

$n$阶微分方程的全解$y(t)$

• $y(t)=y_h(t)+y_p(t)$
• 此时齐次解中还有待定系数$C_i$，$n$阶微分方程需要利用$n$个初始条件$y(0_{+}),y^{\prime }(0_{+}),\dots ,y^{(n-1)}(0_{+})$来确定
• 齐次解$y_h(t)$又被称作自由响应
• 特解$y_p(t)$又被称作强迫响应

自由响应与强迫响应

• 自由响应：仅与系统本身特性有关，而与激励的形式无关，其次解仅与系统特征根有关，特征根成为系统的“固有频率”，齐次解常称为系统的固有响应或自由响应
• 强迫响应：与激励的函数形式有关，特解的形式与激励的形式有关，常称为强迫响应

暂态响应和稳态响应

• 暂态响应：指响应中暂时出现的分量，随着时间增长$t\to \infty$，它将消失$\to 0$

• 稳态响应：指稳定的分量，常以阶跃函数$\epsilon (t)$和周期函数$\sin \omega t,\cos \omega t$等形式存在

• 对于$LTI$连续系统的微分方程$y^{\prime \prime }(t)+5y^{\prime }(t)+6y(t)=\epsilon (t)$以及全响应$y(t)=-e^{-2t}+3$

  • 暂态响应为$-e^{-2t}$，稳态响应为$3$
  • 自由响应为$-e^{-2t}$，强迫响应为$3$

初始状态和初始条件的讨论

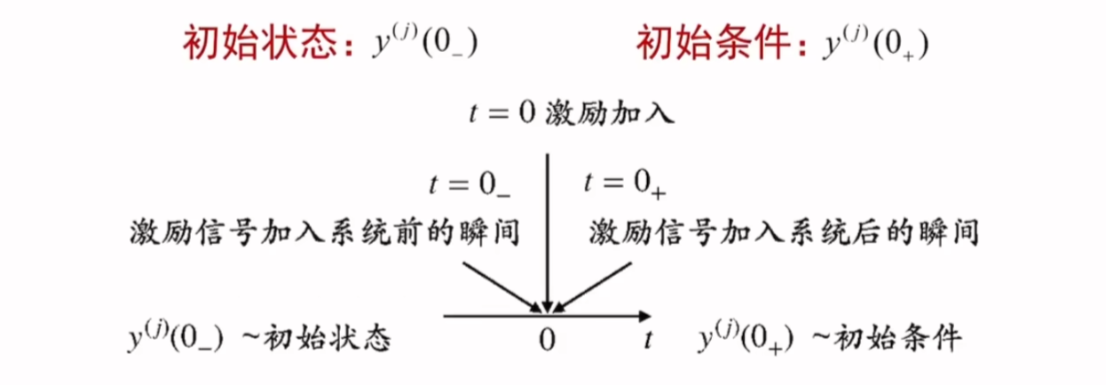
• 实际中，往往先得知系统的初始状态，即先得知激励接入前系统的历史信息
• 由于激励的接入，从$0_{-}$时刻过渡到$0_{+}$时刻之后，初始状态和初始条件往往不一样，我们用跳变量表示这个变化
• 求解微分方程需要从已知的初始状态$y^{(j)}(0_{-})$求得初始条件$y^{(j)}(0_{+})$

基本思路

• 如果激励加入后，在方程右端出现$\delta (t)$及其各阶导数，则在方程左端也应有与之对应的$\delta (t)$及其各阶导数项，使方程两段平衡
• 冲激函数的产生，意味着方程左端$y^{d(i)}(t)$中的某些项在$t=0$处有阶跃的跳变
• 两种求解初始条件的主要方法：待定系数法和冲激平衡法，后续做题主要使用后者

例

某$LTI$连续系统的微分方程为$y^{\prime \prime }(t)+4y^{\prime }(t)+3y(t)=e^{\prime \prime }(t)+2e^{\prime }(t)+e(t)$，已知系统激励$e(t)=\epsilon (t)$，系统的初始状态为$y(0_{-})=0,y^{\prime }(0_{-})=1$，试求系统的初始条件$y(0_{+}),y^{\prime }(0_{+})$

法1：待定系数法

$$\begin{array}{rl}& 设y^{\prime \prime }(t)={\delta }^{\prime }(t)+a\delta (t)+\epsilon (t)\\ & \\ & 积分得y^{\prime }(t)=\delta (t)+a\epsilon (t)y(t)=\epsilon (t)\\ & \\ & 带入原微分方程,只关注冲激项得:\\ & \\ & {\delta }^{\prime }(t)+(4+a)\delta (t)={\delta }^{\prime }(t)+2\delta (t)\\ & \\ & 对比得4+a=2\to a=-2\\ & \\ & 则\{\begin{array}{l}{y}^{\prime }(t)=\delta (t)-2\epsilon (t)\\ \\ y(t)=\epsilon (t)\end{array}\\ & \\ & \{\begin{array}{l}{y}^{\prime }(0_{+})=y^{\prime }(0_{-})+y_e^{\prime }(0_{+})=1-2=-1\\ \\ y(0_{+})=y(0_{-})+y_e(0_{+})=0+1=1\end{array}\end{array}$$

法2：冲激平衡阵列

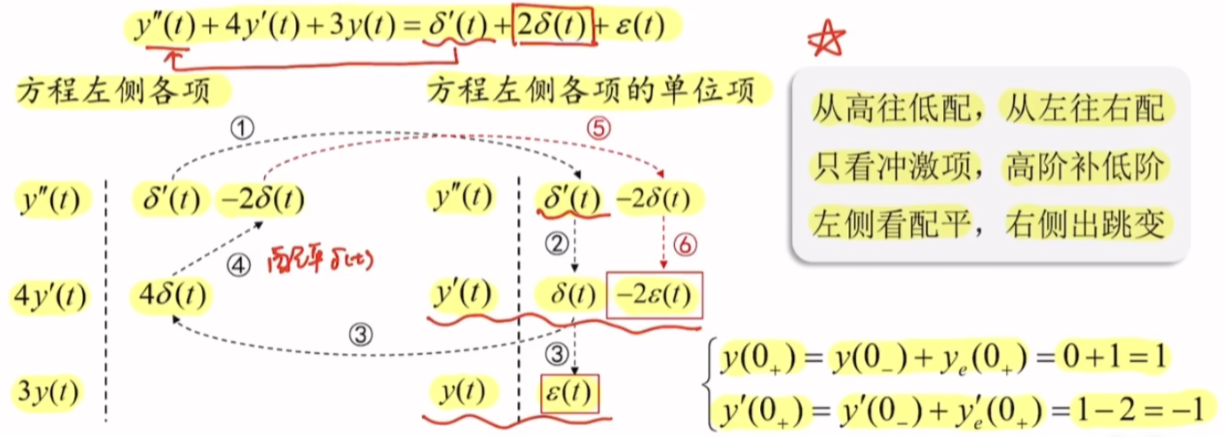
暂时还听不懂这部分，等明白了再回来重新写