【动态规划】卡特兰数

卡特兰数简介

卡特兰数是组合数学中一组极具代表性的数列，由比利时数学家欧仁・查理・卡特兰首次系统研究，因此得名。它在许多看似无关的场景中频繁出现，例如括号匹配、二叉树构造、路径规划等，是解决 “计数类组合问题” 的核心工具之一。

卡特兰数的本质是对 “有约束的选择问题” 中合法方案的计数—— 通常场景是 “两种操作（如‘进’与‘出’、‘左’与‘右’），且某一操作的次数不能超过另一操作”，最终通过 “反射原理” 证明合法方案数为卡特兰数。

卡特兰数与背包问题的区别：

• 卡特兰数与背包问题（0-1 背包、完全背包）虽同属组合计数，但核心差异明显：
  • 背包问题：关注 “在资源约束下（如重量、体积），选择物品的最大价值 / 方案数”，约束是 “资源总量不超过上限”，且物品选择是 “子集 / 多重选择”；
  • 卡特兰数：关注 “两种操作的顺序约束（如左括号 >= 右括号、向右步数 >= 向上步数）”，约束是 “过程中的局部限制”，且方案是 “顺序相关的排列 / 划分”。

---

一、不同的二叉搜索树

题目描述：

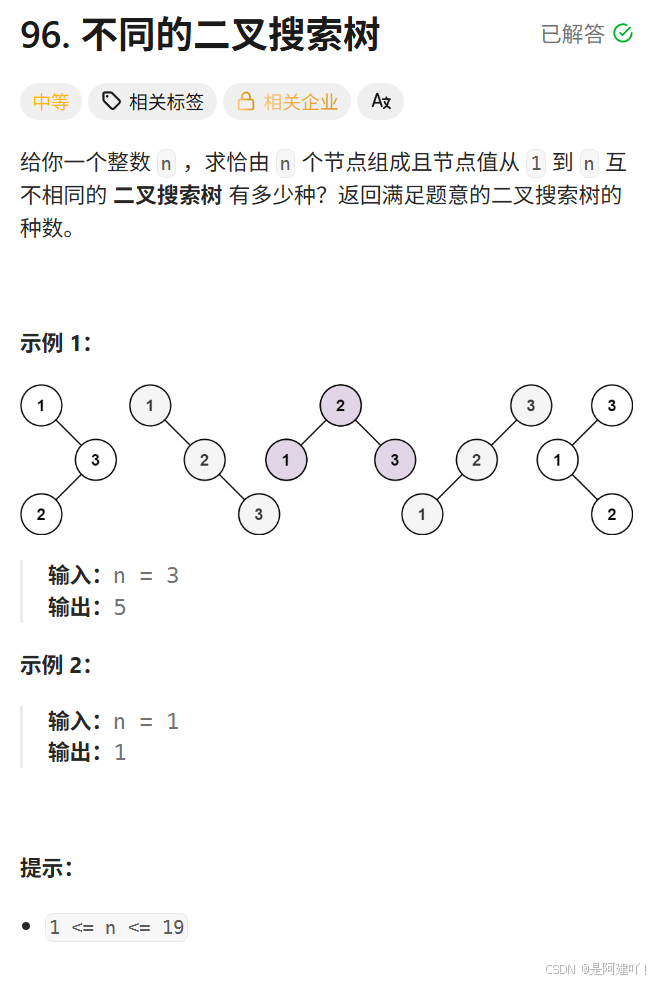
思路讲解：
本道题需要我们根据整数 n ，求恰由 n 个节点组成且节点值从 1 到 n 互不相同的二叉搜索树种数，以下是本道题的具体思路：

1. 状态表示：
   • dp[i]：表示由 i 个节点组成的不同二叉搜索树的种数
2. 状态转移方程：
   • 对于节点数 i，考虑以每个节点 j（1 <= j <= i）作为根节点的情况：
     • 左子树由 j-1 个节点组成，对应的二叉搜索树种数为 dp[j-1]
     • 右子树由 i-j 个节点组成，对应的二叉搜索树种数为 dp[i-j]
     • 以 j 为根的二叉搜索树的种数为左子树和右子树的种数乘积，即 dp[j-1] * dp[i-j]
     • 因此，状态转移方程为：
       • dp[i] = sum(dp[j-1] * dp[i-j])（其中 j 从 1 遍历到 i）
3. 初始化：
   • dp[0] = 1：表示 0 个节点组成的二叉搜索树有 1 种（空树），作为的基础情况
   • 其他 dp[i] 初始为 0：默认初始状态下没有对应的二叉搜索树
4. 填写 DP 表：
   • 外层遍历节点数：i 从 1 到 n，依次计算每个节点数对应的二叉搜索树种数
   • 内层遍历根节点：j 从 1 到 i，依次将每个节点作为根节点，累加对应的二叉搜索树种数
5. 结果返回：
   • 返回 dp[n]，即由 n 个节点组成的不同二叉搜索树的总种数

编写代码：

class Solution {
public:int numTrees(int n) {vector<int> dp(n+1,0);dp[0] = 1;for(int i = 1 ; i <= n ; i++){for(int j = 1 ; j <= i ; j++){dp[i] += dp[j-1] * dp[i-j];}}return dp[n];}
};

---

结尾

如果有什么建议和疑问，或是有什么错误，大家可以在评论区中提出。
希望大家以后也能和我一起进步！！🌹🌹
如果这篇文章对你有用的话，希望大家给一个三连支持一下！！🌹🌹