机器学习笔记

机器学习

监督学习

核心特点

带标签的训练集，主要训练特征与标签之间的对应关系

典型任务：

• 分类（Classification）：预测类别标签（如垃圾邮件识别、图像分类）

• 回归（Regression）：预测连续数值（如房价预测、温度预测）

非监督学习

核心特点

使用无标签的数据训练模型，模型需要自主发现数据中的规律

典型任务

• 聚类（Clustering）：将相似数据分组（如用户分群、异常检测）；

• 降维（Dimensionality Reduction）：简化数据特征同时保留关键信息（如 PCA 算法）；

• 生成式模型（Generative Models）：生成与训练数据相似的新数据（如 GAN 生成图像）。

线性回归模型(监督学习)

定义

核心是用一条直线（或高维空间中的平面） 来拟合数据，从而预测连续数值结果。

例：

训练集

收集房屋面积$x$以及房价$y$，训练模型预测房屋面积对应的房价。

模型表示

此时线性回归模型可概括成:$y=w\times x+b$

训练目标

找到最合适的参数$w,b$，使得预测的结果与真实值误差最小

代价函数(Cost Function)

对于线性回归模型，一般以均方误差描述(MSE)，描述如下：

$J(w,b)=\frac{1}{2m}\sum _{i=1}^m({\hat{y}}^{(i)}-y^{(i)}{)}^2$

即：

$J(w,b)=\frac{1}{2m}\sum _{i=1}^m(f_{w,b}(x{)}^{(i)}-y^{(i)}{)}^2$

其中，$J(w,b)$为代价函数，$m$为训练集的数据数量，${\hat{y}}^{(i)}$为为第$i$组数据的预测结果，$y^{(i)}$为第$i$组数据的实际结果，$f(w,b)$为构建的线性回归模型。

注： 随便训练集中仅包含$m$个数据，但由于此时取均方误差，那么后续进行梯度求导时为了将乘上的$2$抵消，此时分母多乘一个$2$，取$2m$。

梯度下降(Dradient Descent)

不难想到，想要使得模型预测的结果更加准确，那么就是要使得代价函数计算的结果尽可能的小，因此，使用梯度下降来对所有参数进行同步操作。

公式

$Gradientdescent$

$repeat${

• $w_j=w_j-\alpha \frac{\delta }{\delta w_j}J(w_1,\dots ,w_n,b)$

• $b=b-\alpha \frac{\delta }{\delta b}J(w_1,\dots ,w_n,b)$

}

即重复操作参数直到模型收敛，其中$\alpha$为学习率，可以理解为步长，即梯度下降过程中每一步的长度。

注：不难发现，每次减去的值均需用到模型中所有参数，那么如果在更新参数的过程中修改了参数，就会导致后续参数更新出错，因此，需要在计算完所有结果后再进行更新，中间值可以用临时变量记录。

如下：

先用临时变量记录修改后的参数

• $tm{p}_{w_1}=w_1-\alpha \frac{\delta }{\delta w_j}J(w_1,\dots ,w_n,b)$

• $\dots$

• $tm{p}_{w_n}=w_n-\alpha \frac{\delta }{\delta w_j}J(w_1,\dots ,w_n,b)$

• $tm{p}_b=b-\alpha \frac{\delta }{\delta b}J(w_1,\dots ,w_n,b)$

将结果恢复到模型中

• $w_1=tm{p}_{w_1}$

• $\dots$

• $w_n=tm{p}_{w_n}$

• $b=tm{p}_b$

解析

下图给出了一个代价函数的图像，假设横坐标表示模型的参数，纵坐标表示模型参数对应的代价函数的值。

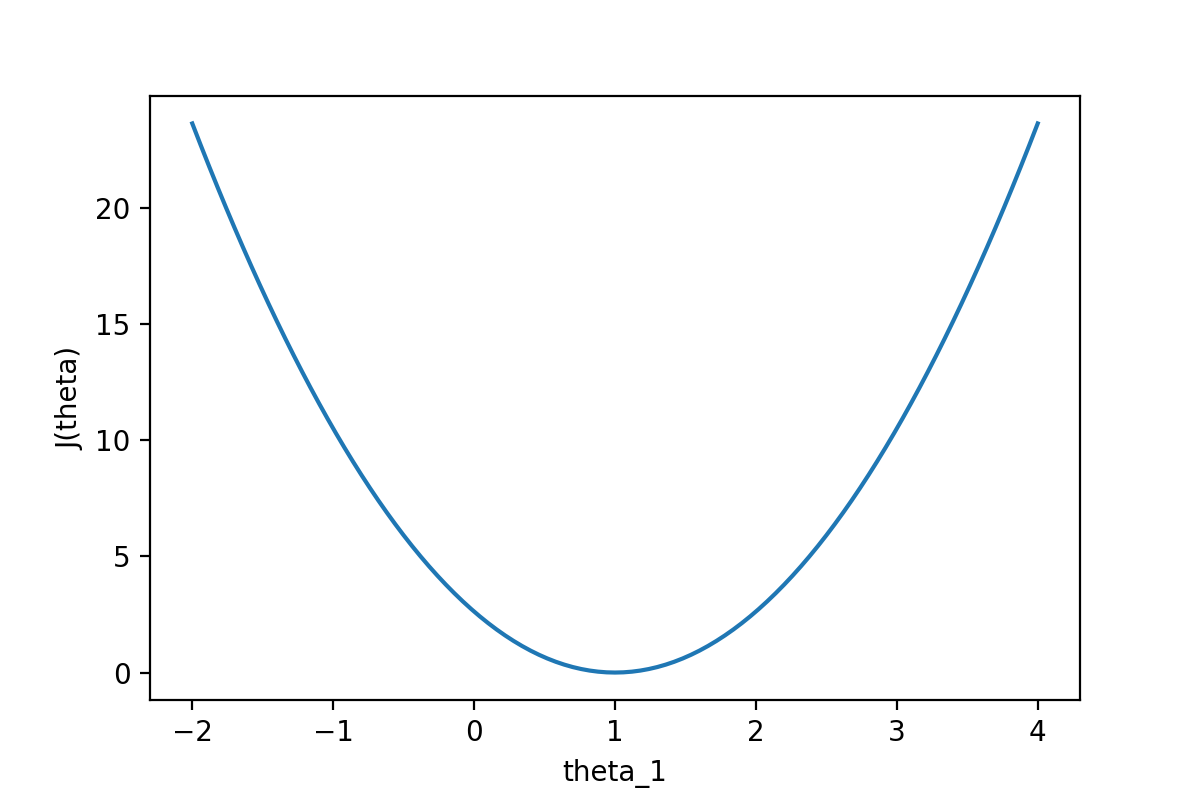
为什么通过前面的公式可以实现模型训练呢？

对于该图像而言，想要模型预测误差最小，必然选择代价函数对应值最低的点，但是要怎么让计算机找到该点呢？

那么不难想到，我们既然要找最低点，最容易的方法就是在当前函数递增时后退，递减时前进，那么怎么走都会来到更低点。

那么前面公式中的$-\alpha \frac{\delta }{\delta w_j}J(w_1,\dots ,w_n,b)$就可以解释了，对代价函数求导，当代价函数递增时，此时导数必然大于$0$，即$\frac{\delta }{\delta w_j}J(w_1,\dots ,w_n,b)>0$，由于学习率$\alpha$必然是个正数，此时参数减去的值也就必然是个正数，更新完成后必然使得此时代价函数的结果更小。

如下图所示，一次操作相当于向谷底走了一步。

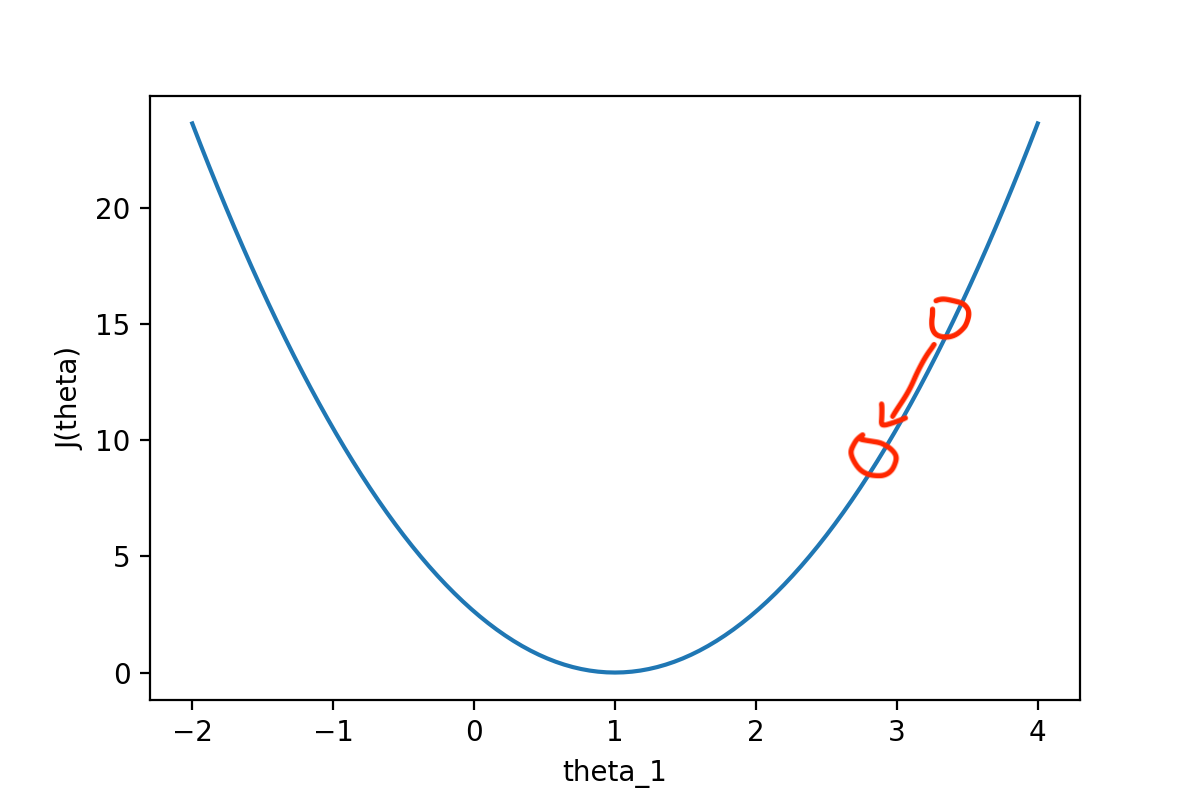
反之同理。

怎么判断梯度下降是否收敛

可以设置一个极小值$ϵ=0.001$，当代价函数减少的值小于$ϵ$时，我们就可以认为此时模型已经收敛。

注

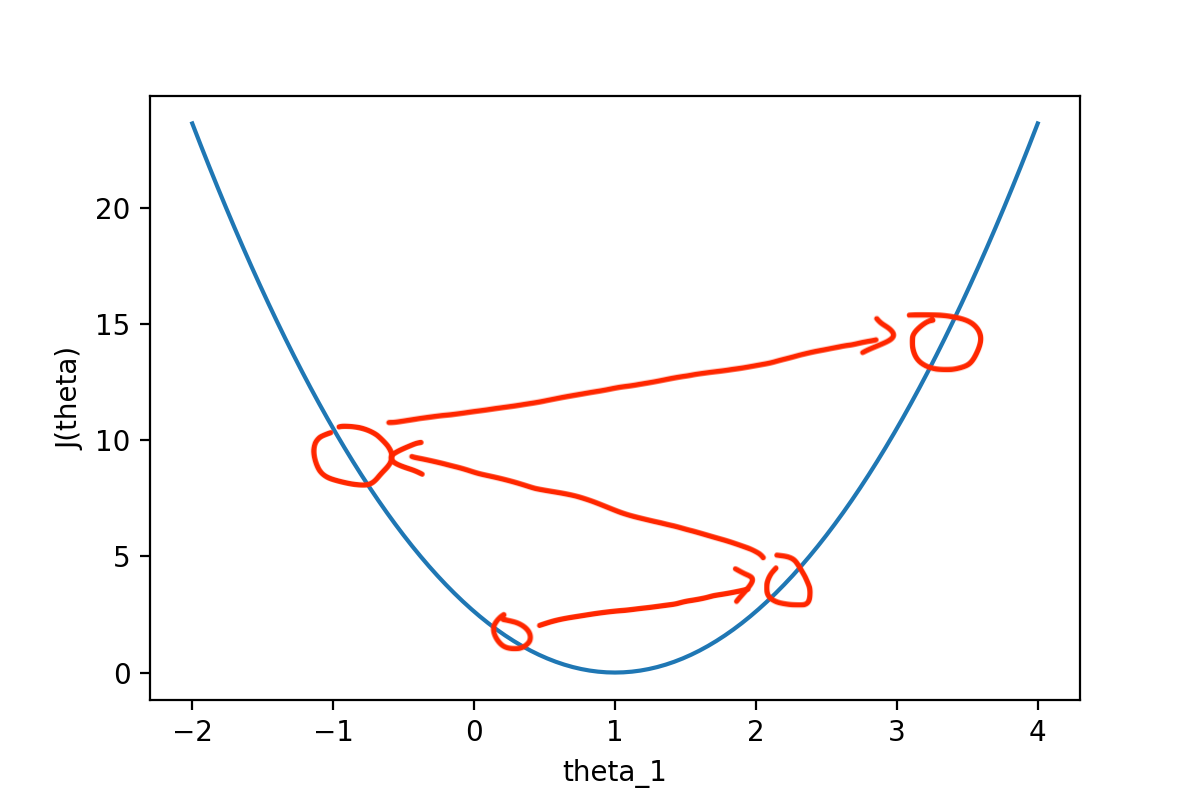
不难发现，梯度下降算法本质上就是一种贪心算法，每一次从当前位置找到能下降最快的路径，并走出一步，那么如果图像存在多个凹点，对于选择到不同的起点，最后收敛的位置实际上是不一样的，因此，起点的选择也十分重要。

同时，如果学习率过大，也可能导致每次操作会在图像两边反复横跳。

学习率(learning rate)

定义

从简单的角度思考，学习率实际上就意味着每次向最低走移动的步长，不难想到如果学习率过大，那么可能导致模型无法拟合，而学习率过小，又会导致模型训练效率降低。

学习率的选择

因此，可以依次测试学习率，如，依次尝试：

• $\dots ,0.001,0.01,0.1,1,\dots$

当然，也可以依次在中间添加一些值，如在$0.001$和$0.01$之间添加$0.003$, $0.01$和$0.1$之间添加$0.03$，使得每个学习率之间的差不多差$3$倍。

向量化

将参数向量化后，就可以利用计算机强大的并行计算能力，优化代码的执行时间。

如使用python中的numpy库：

import numpy as np
w = np.array([1.0, 2.5, -3.3])
b = 4
x = np.array([10, 20, 30])
f = np.dot(w, x) + b #向量点乘

特征缩放

当不同特征的数据范围差距较大时，如$0\le x_1\le 1,300\le x_2\le 2000$，此时绘制出的代价函数就会是个非常细长的椭圆形，也就意味着进行梯度下降时，尽管特征$x_1$每一步移动的都很小，特效$x_2$每一步都会移动很大。梯度下降的过程就会反复横跳，经过很多时间之后才会收敛。

常用缩放方法

1. 直接让所有参数处以他们的最大值，这样所有参数的数据范围都会来到$0\sim 1$之间。

2. 均值归一化：

找到训练集中每个参数的平均数，定义$x_1,{\mu }_1,max(x_1),min(x_1)$表示参数，该参数均值，该参数中的最大最小值，并进行修改得到：

• $x_1=\frac{x_1-{\mu }_1}{max(x_1)-min(x_1)}$

即使得该参数的每个值减去均值后处以最大值与最小值的差值。

3. Z-score normalization

取参数$x_1$的均值${\mu }_1$，标准差${\sigma }_1$，另该参数中每一个数据减去均值后处以标准差，即：

• $x_1=\frac{x_1-{\mu }_1}{{\sigma }_1}$

特征工程

当当前特征可能无法正确预测结果时，可以创建一些新的特征加入模型，这样，经过训练后，可能使得模型更加拟合。

分类

与回归通过若干特征得到多种结果不同，分类取得的结果是固定的，即类似于选择题，模型在阅读完特征后，在给出的选项中选出对应的结果。

逻辑回归

为解决分类问题，线性回归无法很好的完成，因此引入$sigmoid$函数用于解决分类问题。

以下以结果仅包含$0,1$的数据集为例。

定义

• $g(z)=\frac{1}{1+e^{-z}},0<g(z)<1$

其中，$z=f_{\vec{w},b}(\vec{x})$

此时，$f_{\vec{w},b}(\vec{x})=P(y=1|\vec{x};\vec{w},b)$，即表示该组数据为真的概率。

逻辑回归的损失函数

$$L(f_{\vec{w},b}({\vec{x}}^{(i)}),y^{(i)})=\{\begin{array}{ll}-log(f_{\vec{w},b}({\vec{x}}^{(i)}))& \text{if }{y}^{(i)}=1,\\ -log(1-f_{\vec{w},b}({\vec{x}}^{(i)}))& \text{if }{y}^{(i)}=0.\end{array}$$

代价函数简化

由于$y^{(i)}$仅存在$0,1$两种可能的值，因此可以构造一个函数使得满足损失函数。

$L(f_{\vec{w},b}({\vec{x}}^{(i)}),y^{(i)})=-y^{(i)}log(f_{\vec{w},b}({\vec{x}}^{(i)}))-(1-y^{(i)})log(1-f_{\vec{w},b}({\vec{x}}^{(i)}))$

代价函数

由于此时没有平方项，那么此时代价函数分母不需要再乘上一个2.

$$\begin{array}{rl}J(\vec{w},b)& =\frac{1}{m}\sum _{i=1}^m[L(f_{\vec{w},b}({\vec{x}}^{(i)}),y^{(i)})]\\ & =-\frac{1}{m}\sum _{i=1}^m[y^{(i)}log(f_{\vec{w},b}({\vec{x}}^{(i)}))+(1-y^{(i)})log(1-f_{\vec{w},b}({\vec{x}}^{(i)}))]\end{array}$$

梯度下降

此时对代价函数求导可得：

• $\frac{\delta }{\delta w_j}J(\vec{w},b)=\frac{1}{m}\sum _{i=1}^m(f_{\vec{w},b}({\vec{x}}^{(i)})-y^{(i)})x_j^{(i)}$

• $\frac{\delta }{\delta b}J(\vec{w},b)=\frac{1}{m}\sum _{i=1}^m(f_{\vec{w},b}({\vec{x}}^{(i)})-y^{(i)})$

则剩余梯度下降操作与线性回归一致

决策边界

简单来说，就是通过决策边界，让模型可以判断数据落在决策边界的哪一边，来确定数据属于哪一类别。

线性决策边界

• 边界方程：$w_1{x}_1+w_2{x}_2+\dots +w_n{x}_n+b=0$

过拟合

模型对训练集数据表现极好，但对未见过的测试数据表现极差。本质原因是"模型复杂度" 超过了 “数据所能支撑的复杂度”。

解决方法

1. 增加训练集中数据

2. 选择性的使用数据中的特征

3. 使用正则化减少参数的大小

正则化代价函数

引言

普通的代价函数追求最小化模型预测值与真实值的差距，而这可能导致模型为了 “完美拟合训练数据” 而变得过于复杂（例如参数值过大、多项式次数过高），最终出现过拟合。

例

当前模型：

• $f_{w,b}(x)=w_{1}x+w_2{x}^2+w_3{x}^3+w_4{x}^4+b$

不难发现此时$x^3,x^4$对结果的影响是非常大的，那么为了避免模型出现过拟合的问题，必然需要尽可能缩小$w_3,w_4$的取值。

此时可以加上一些惩罚项，即在代价函数中增加：

• $1000\times w_3^2+1000\times w_4^2$

即代价函数变为：

• $J(\vec{w},b)=\frac{1}{2m}\sum _{i=1}^m(f_{\vec{w},b}(x^{(i)})-y^{(i)}{)}^2+1000\times w_3^2+1000\times w_4^2$

由于$w_3,w_4$都会乘上一个较大的参数，同时开了平方避免出现负数，那么为了尽可能减小代价函数，$w_3,w_4$所能取得值必然是一个较小的数字，避免影响模型出现过拟合。

正则化

实际上在模型训练前，我们不知道哪些参数对模型来说是至关重要的，因此最好的方法就是对所有参数均执行一些惩罚。

即：

• $J(\vec{w},b)=\frac{1}{2m}\sum _{i=1}^m(f_{\vec{w},b}(x^{(i)})-y^{(i)}{)}^2+\frac{\lambda }{2m}\sum _{j=1}^n{w}_j^2$

这里的$\lambda$为正则化参数，$\lambda$的选择也至关重要，当$\lambda$较小，可能导致过拟合，较大，可能导致铅拟合。

正则化后的梯度下降

• $\frac{\delta }{\delta w_j}J(\vec{w},b)=\frac{1}{m}\sum _{i=1}^m(f_{\vec{w},b}({\vec{x}}^{(i)})-y^{(i)})x_j^{(i)}+\frac{\lambda }{m}{w}_j$

• $\frac{\delta }{\delta b}J(\vec{w},b)=\frac{1}{m}\sum _{i=1}^m(f_{\vec{w},b}({\vec{x}}^{(i)})-y^{(i)})$