Neumann Networks for Linear Inverse Problems in Imaging论文阅读

1. 研究目标与实际意义

目标：提出一种名为 Neumann Network（NN） 的端到端数据驱动方法，用于解决成像中的线性逆问题（如去模糊、解卷积、修复、压缩感知和超分辨率）。核心是通过截断 Neumann 级数直接求解带非线性正则化器的逆问题，而非展开迭代优化算法。
实际问题：传统正则化器（如平滑性或稀疏性假设）难以捕捉复杂图像先验，而数据驱动方法需大量样本学习完整图像空间。NN 通过显式结合前向算子 $X$，显著降低样本复杂度，适用于医学成像等小数据集场景。
产业意义：提升图像重建质量（如医学影像诊断精度），降低深度学习对数据量的依赖，加速实时成像应用（如 MRI 重建）。

---

2. 创新方法：Neumann Network及其理论实现

2.1 核心思路：Neumann级数展开与传统逆问题的结合

传统线性逆问题表示为：
$$y=X{\beta }^{\star }+ϵ$$
目标最小化正则化最小二乘问题：
$$\hat{\beta }=\arg \underset{\beta }{\min }\frac{1}{2}\Vert y-X\beta {\Vert }_2^2+r(\beta )\text{\hspace{1em}(2)}$$ 图2：Neumann 网络架构（跳跃连接为红色路径）

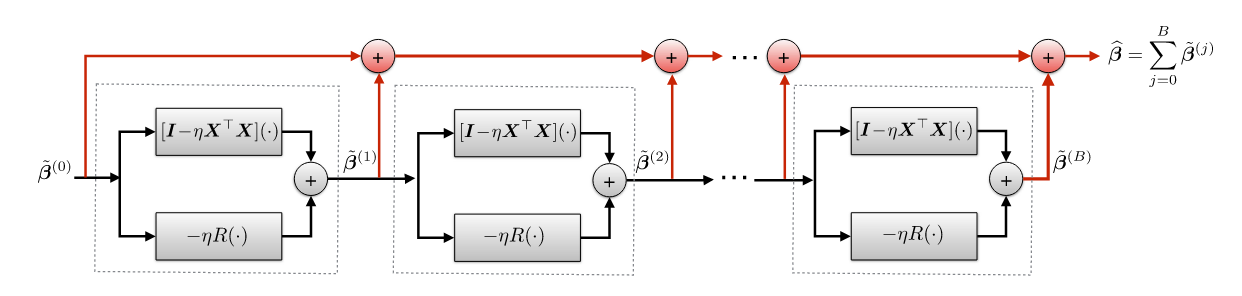
核心创新：

• Neumann级数直接近似逆矩阵：
  论文将解 ${\beta }^{\star }=(X^{\top }X+R{)}^{-1}{X}^{\top }y$（公式5）通过Neumann级数展开（公式7）：
  $$B^{-1}=\eta \sum _{k=0}^{\infty }(I-\eta B{)}^k\text{where}B=X^{\top }X+R\text{\hspace{1em}(7)}$$
  代入后得到迭代形式（公式8）：
  $${\beta }^{\star }=\sum _{j=0}^{\infty }(I-\eta X^{\top }X-\eta R{)}^j(\eta X^{\top }y)\text{\hspace{1em}(8)}$$
• 数据驱动正则化器：
  将线性算子 $R$ 替换为非线性神经网络 $R_{\theta }$，形成Neumann网络（公式9）：
  $$\hat{\beta }(y)=\sum _{j=0}^B([I-\eta X^{\top }X$$