基于遗传算法优化BP神经网络的时间序列预测 GA-BP
一、作品详细简介
1.1附件文件夹程序代码截图

全部完整源代码,请在个人首页置顶文章查看:
学行库小秘_CSDN博客![]() https://blog.csdn.net/weixin_47760707?spm=1000.2115.3001.5343
https://blog.csdn.net/weixin_47760707?spm=1000.2115.3001.5343
1.2各文件夹说明
1.2.1 main.m主函数文件
以下是对该MATLAB代码的详细分步解释,涵盖了从数据导入到模型评估的全过程:这段代码实现了一个基于遗传算法(GA)优化反向传播(BP)神经网络的时间序列预测模型。
代码整体流程概述
- 数据准备与预处理:读取数据,构造用于监督学习的数据集,并划分训练集和测试集。
- 数据归一化:将数据缩放至[0, 1]区间,加速神经网络收敛并提高精度。
- 模型建立与优化:
- 初始化一个BP神经网络。
- 使用遗传算法优化该神经网络的初始权重和偏置。
- 模型训练与预测:用优化后的参数训练网络,并对训练集和测试集进行预测。
- 结果评估与可视化:计算多项评估指标(RMSE, R², MAE, MBE)并绘制图表分析预测性能。
详细分步解释
第一步:数据导入与路径设置
- xlsread 从 数据集.xlsx 文件中读取数据,存储到变量 result 中。假设数据是单列的时间序列。
- addpath 将 goat 文件夹添加到MATLAB的搜索路径中。这个文件夹 likely 包含了后续要使用的遗传算法相关函数(如 gabpEval, gadecod, initializega)。
第二步:数据分析与参数设置
第三步:构造数据集
标输出):result(i + kim + zim - 1),即紧接着15个点之后的第 zim 个点(这里就是第16个点)。
- 最终,res 是一个矩阵,每一行前15列是输入特征,第16列是目标值。
第四步:划分训练集和测试集
- 将922个样本划分为700个训练样本和222个测试样本。
- P_train 和 P_test 是输入特征矩阵,维度为 15 x N(N是样本数)。
- T_train 和 T_test 是目标输出向量,维度为 1 x N。
第五步:数据归一化
- mapminmax 函数将数据线性归一化到[0, 1]区间。
- 首先对训练集输入 P_train 进行归一化,得到 p_train,并保存归一化参数 ps_input。
- 然后使用 ps_input 对测试集输入 P_test 进行相同的归一化(非常重要,避免数据泄露)。
- 对目标值 T_train 和 T_test 进行同样的操作。
第六步:建立初始BP神经网络模型
- newff 创建一个前馈神经网络(Feedforward Neural Network)。
- 输入是归一化后的训练数据 p_train 和 t_train。
- S1 定义了隐藏层的神经元数量(这里为5)。该网络结构为:输入层(15) -> 隐藏层(5, 默认tansig函数) -> 输出层(1, 默认purelin函数)。
第七步:设置神经网络训练参数
第八步:遗传算法(GA)参数设置
- S 计算了需要优化的参数总数(所有权重和偏置):
- size(p_train,1)*S1:输入层到隐藏层的权重数量 (15 * 5)
- S1*size(t_train,1):隐藏层到输出层的权重数量 (5 * 1)
- S1:隐藏层的偏置数量 (5)
- size(t_train,1):输出层的偏置数量 (1)
- S = 15*5 + 5*1 + 5 + 1 = 86
- bounds 定义了86个参数的搜索空间。
第九步:初始化遗传算法种群
- initializega 函数生成初始种群。每个个体都是一个长度为86的向量(代表神经网络的所有参数),其值在[-1,1]内随机生成。
- 'gabpEval' 是适应度函数,GA用它来评估每个个体的好坏。
第十步:运行遗传算法进行优化
- ga 函数执行遗传算法优化。
- 核心过程是:对于每一代种群,用 gabpEval 函数计算每个个体的适应度。这个函数 likely 的工作流程是:
- 将个体染色体解码为神经网络的权重和偏置(W1, B1, W2, B2)。
- 将这些参数赋给神经网络(net)。
- 神经网络使用当前参数(不训练)对训练集进行一次前向传播(仿真)。
- 计算仿真输出与真实值的均方误差(MSE)。
- 适应度值通常设为 1 / MSE(误差越小,适应度越高)。
- 遗传算法通过选择、交叉、变异等操作,不断进化种群,寻找能使适应度最高(即误差最小)的个体。
- Bestpop 是最终得到的最优个体(染色体)。
- trace 记录了进化过程中每代的最优适应度值。
第十一步:解码最优个体并赋值给网络
- gadecod 函数将最优染色体 Bestpop 解码成神经网络可用的权重矩阵和偏置向量。
- 将这些优化后的参数直接赋予神经网络,为后续训练提供一个非常好的初始点。
第十二步:训练神经网络
- 使用 train 函数(通常采用梯度下降法,如LM算法)对网络进行训练。
- 由于初始权重和偏置已经被GA优化过,训练过程会更快收敛,且更有可能找到全局最优解附近,避免了传统BP网络容易陷入局部最小值的问题。
第十三步:仿真预测
- sim 函数使用训练好的网络进行预测(前向传播)。
第十四步:数据反归一化
- 将归一化后的预测结果 t_sim1 和 t_sim2 转换回原始数据尺度,得到最终的预测值 T_sim1 和 T_sim2。
第十五步:评估模型性能
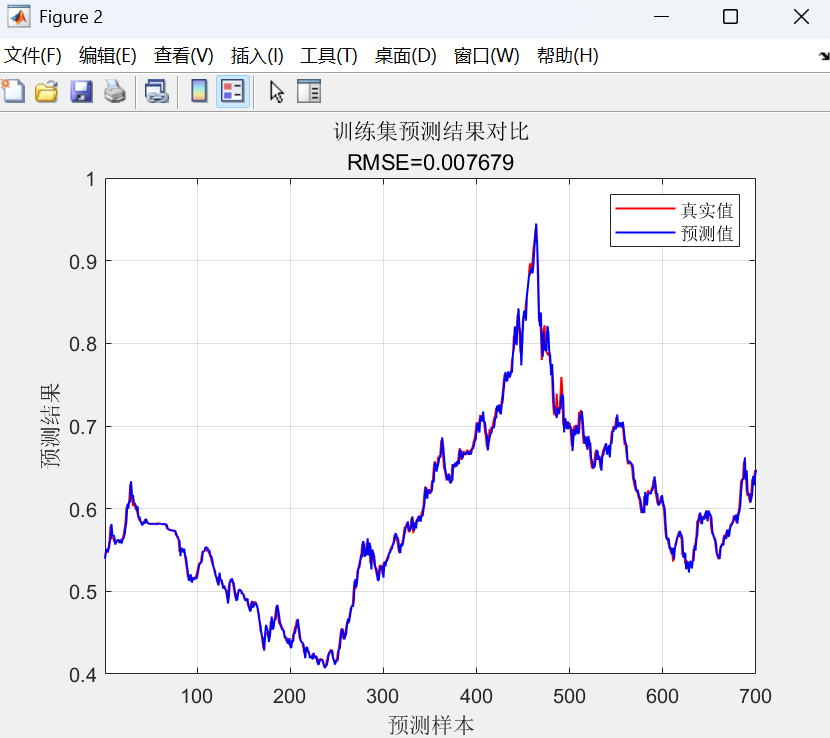
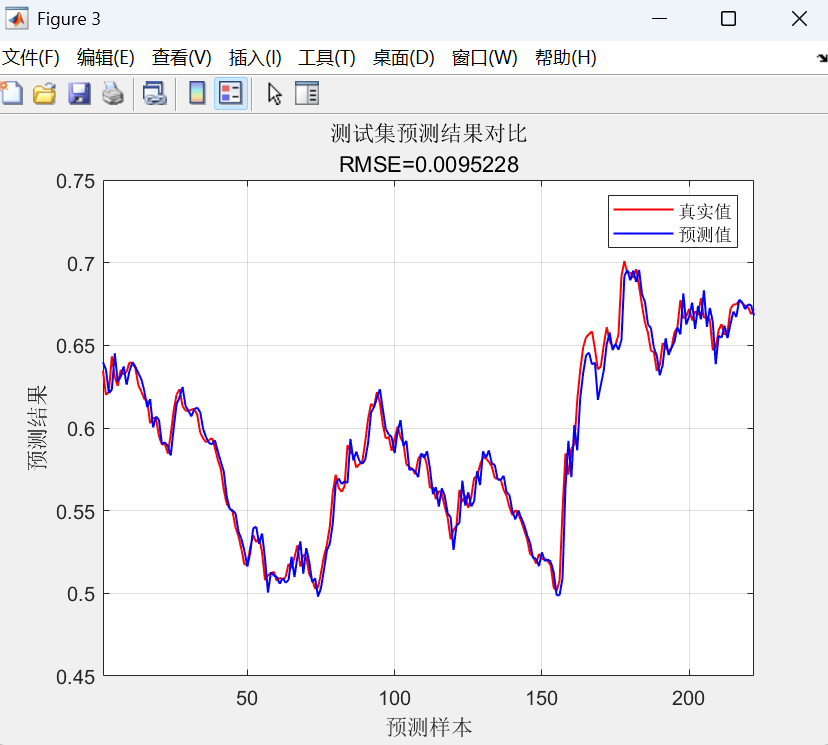
- RMSE: 衡量预测值与真实值之间的偏差,越小越好。
- R²: 表示模型对数据方差的解释程度,越接近1越好。
- MAE: 另一种衡量平均绝对误差的指标。
- MBE: 衡量预测偏差的平均值,正负表示系统性偏高或偏低。
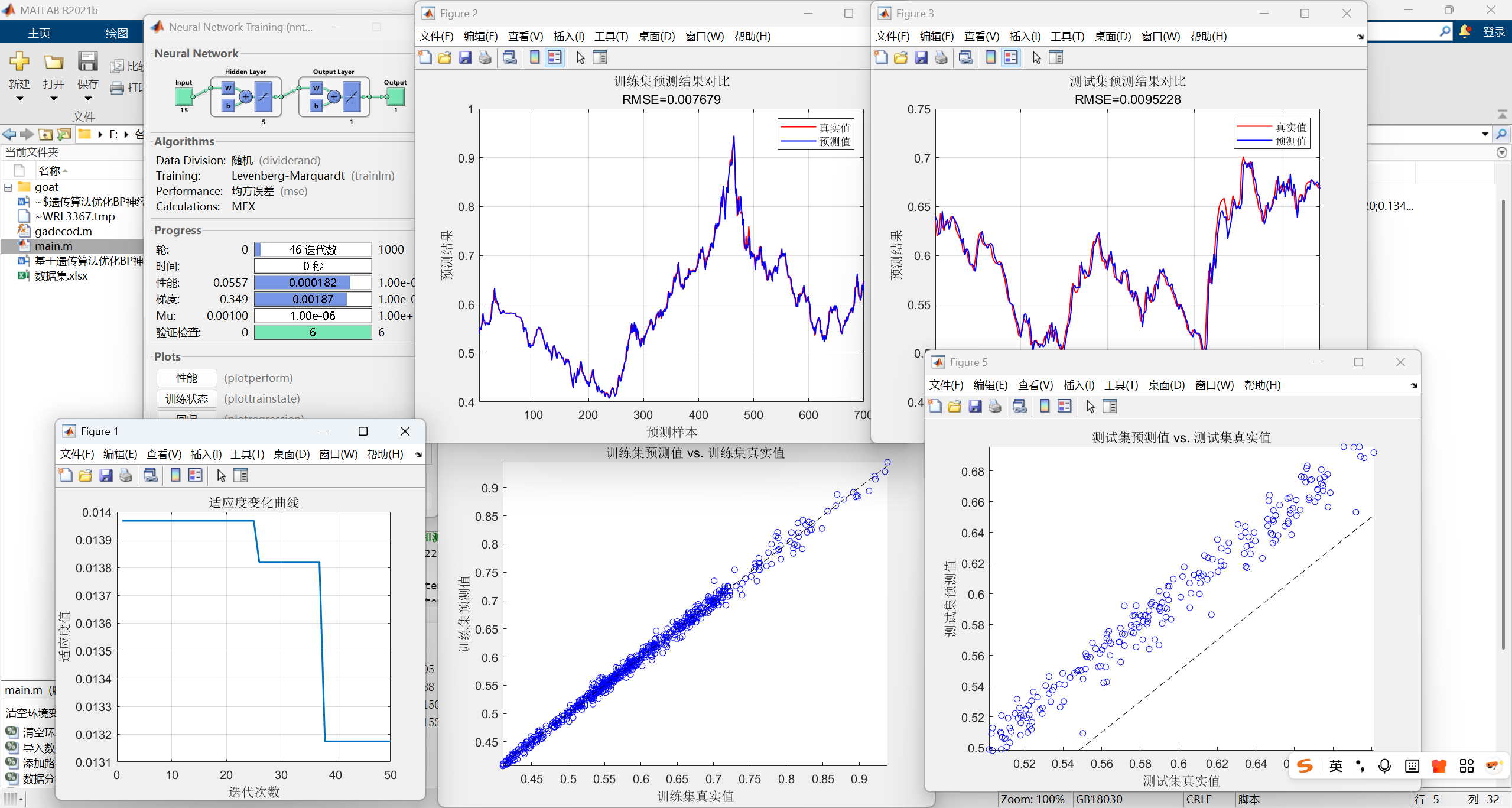
第十六步:可视化结果
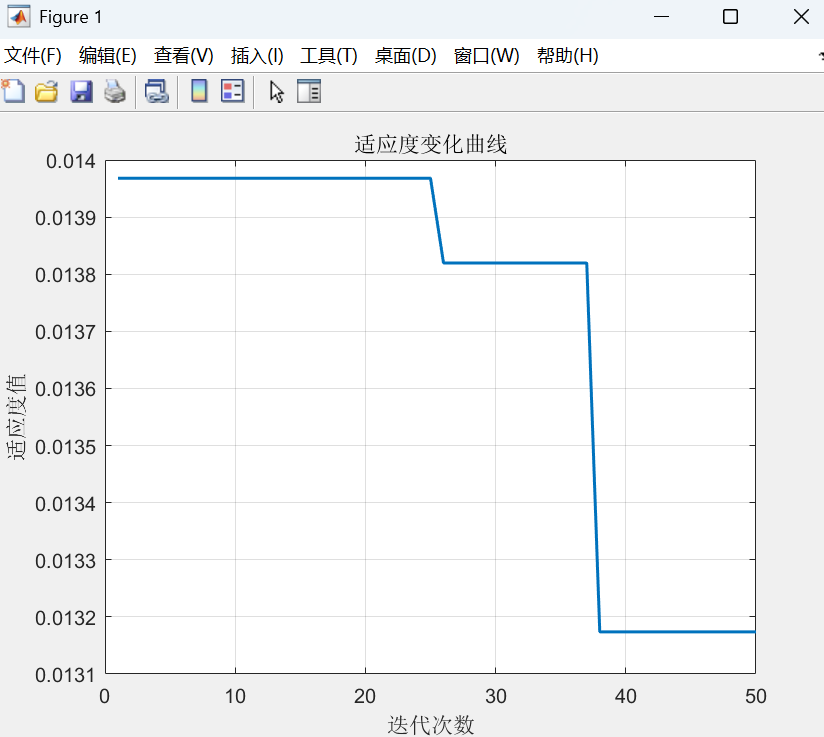
- 适应度曲线:绘制遗传算法进化过程中适应度的变化,观察优化过程。
- 预测对比图:分别绘制训练集和测试集上真实值与预测值的对比曲线,并标注RMSE。
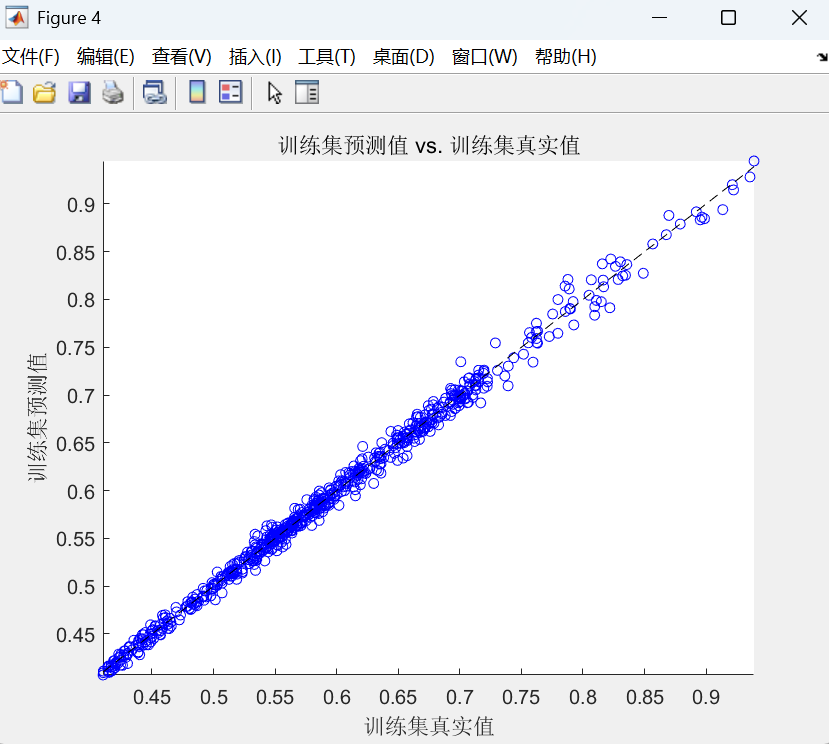
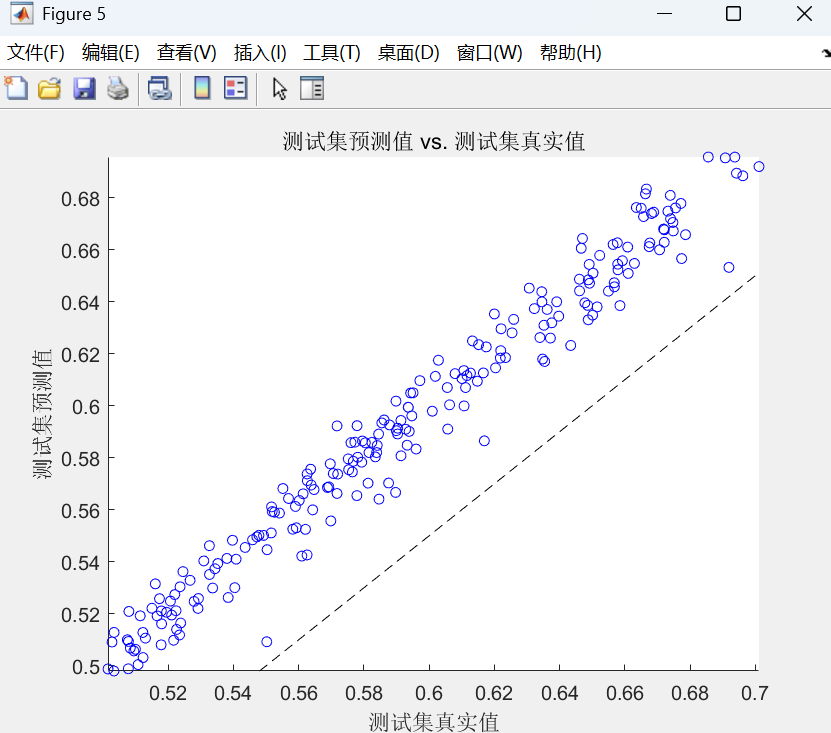
- 散点图:绘制预测值与真实值的散点图,并添加y=x的参考线。点越集中在对角线附近,预测越准确。
总结
这段代码的核心创新点在于将遗传算法(全局搜索优势) 与BP神经网络(局部精确搜索优势) 相结合(GA-BP模型)。
- 遗传算法负责在全局范围内为神经网络寻找一组优秀的初始权重和偏置。
- BP算法在此基础上进行精细调整,完成最终的训练。
这种混合策略有效解决了传统BP神经网络对初始值敏感、容易陷入局部最小值的问题,从而提高了模型的预测精度和稳定性。代码后续通过详细的误差指标和多种图表对模型的性能进行了全面的评估和展示。
图2 main.m主函数文件部分代码
1.2.2 数据集文件
数据集为Excel数据csv格式文件,可以方便地直接替换为自己的数据运行程序。原始数据文件包含1列时间序列数据,一共包含937个样本数据,具体如图所示。
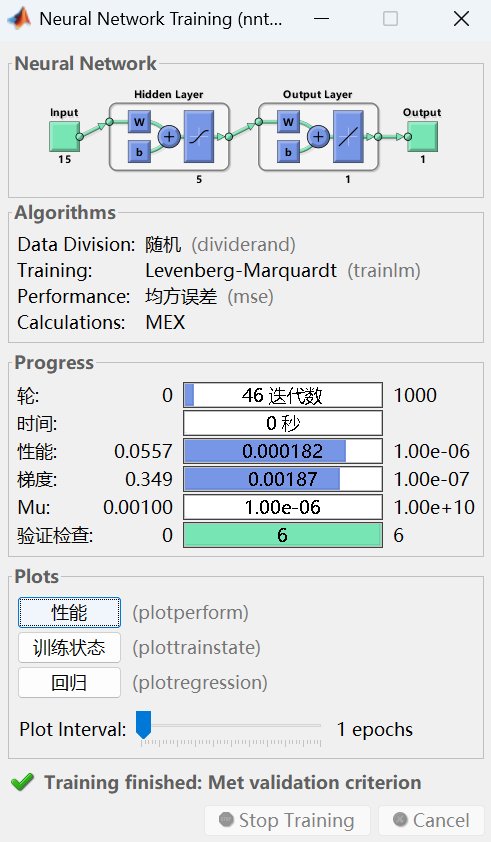
二、代码运行结果展示
这段代码实现了一个基于遗传算法优化BP神经网络的时间序列预测模型。
首先,代码读取数据并构造训练集和测试集,对数据进行归一化预处理;
其次,利用遗传算法全局搜索神经网络的最优初始权重和偏置参数,并将这些参数赋给网络;
最后,使用优化后的网络进行训练和预测,通过反归一化得到最终结果,并计算多种评估指标和绘制图表来全面评估模型性能。
三、注意事项:
1.程序运行软件推荐Matlab 2018B版本及以上;
2.所有程序都经过验证,保证程序可以运行。此外程序包含简要注释,便于理解。
3.如果不会运行,可以帮忙远程运行原始程序以及讲解和其它售后,该服务需另行付费。
4. 代码包含详细的文件说明,以及对每个程序文件的功能注释,说明详细清楚。
5.Excel数据,可直接修改数据,替换数据后直接运行即可。
