力扣498 对角线遍历

力扣498 对角线遍历

问题分析

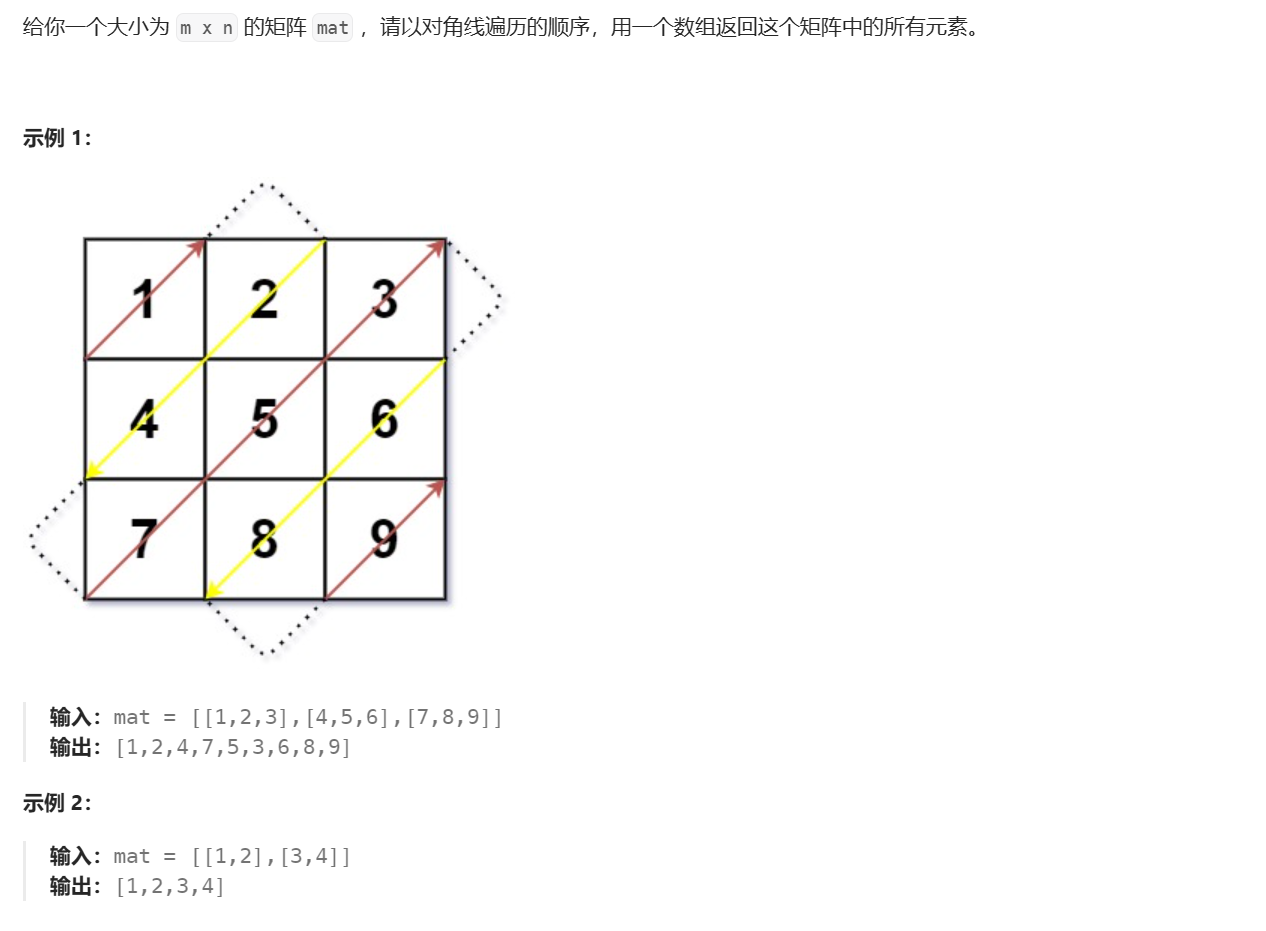
给定一个 m x n 矩阵，我们需要按照对角线顺序遍历所有元素。对角线遍历的特点是：

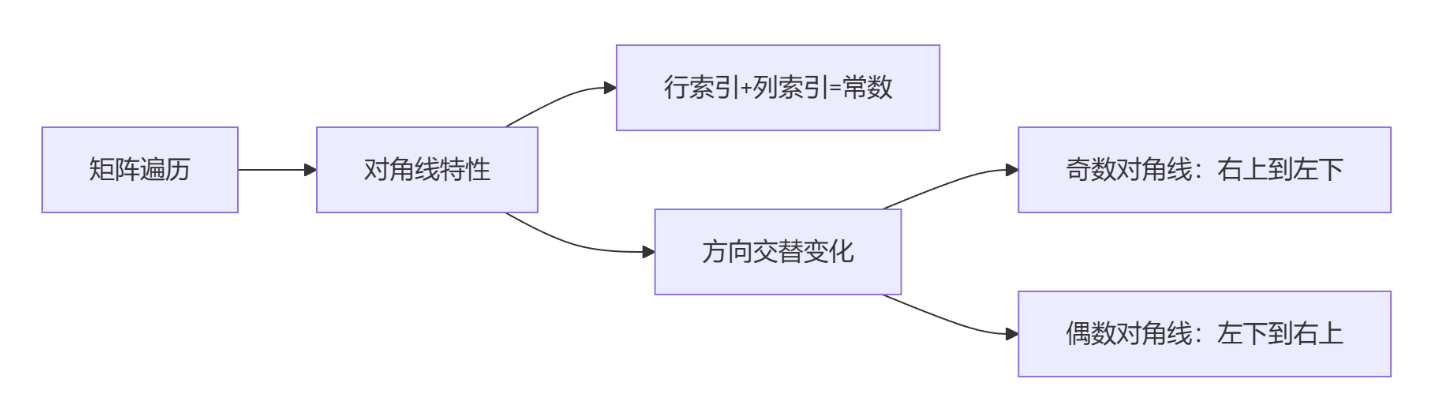
• 每条对角线上元素的行索引与列索引之和为常数
• 遍历方向交替变化：奇数对角线（从右上到左下），偶数对角线（从左下到右上）

解决方案

核心思路

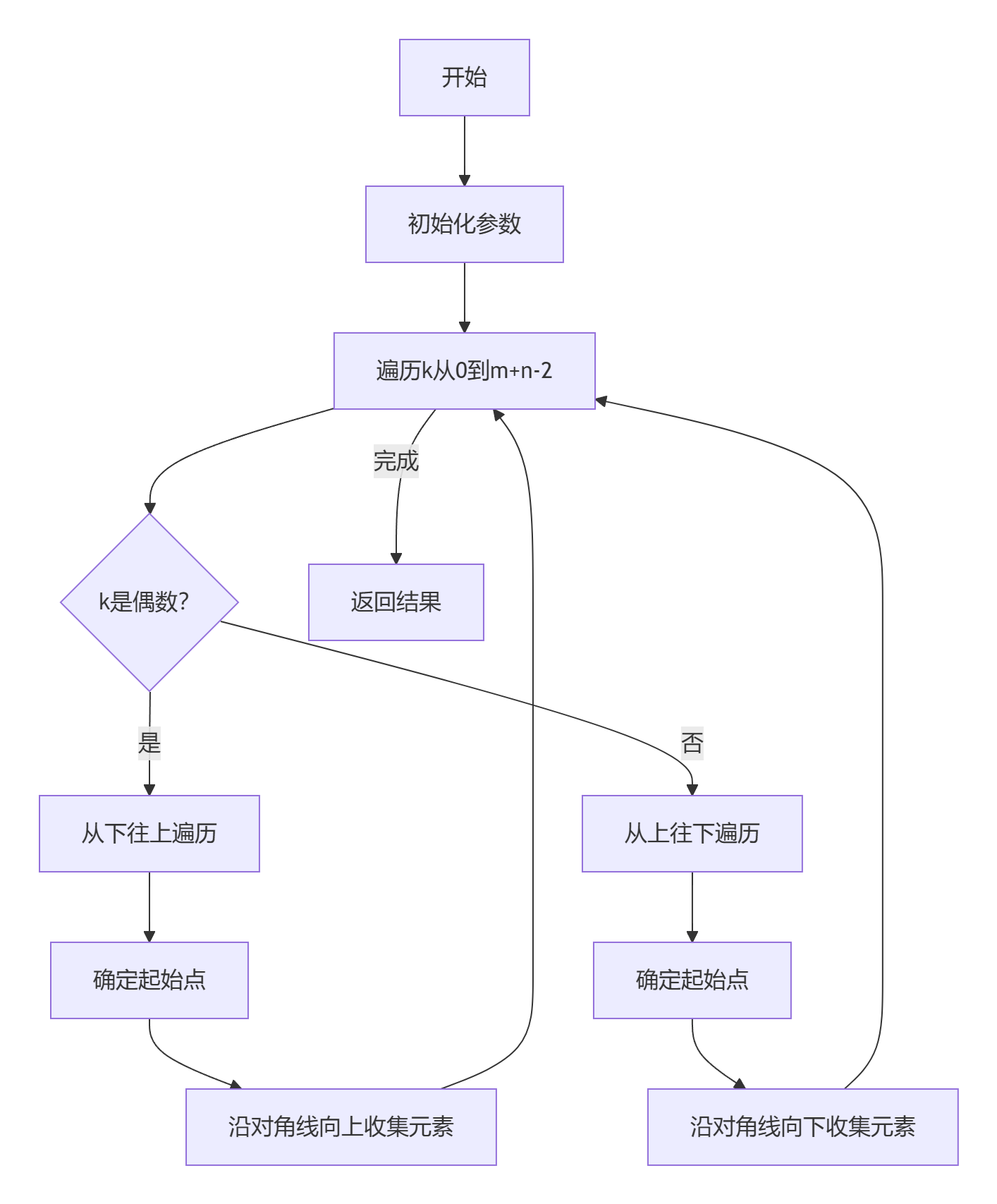
1. 确定对角线常数k：从0到(m-1)+(n-1)
2. 根据k的奇偶性确定遍历方向：
   • k为偶数：从下往上遍历（行索引递减，列索引递增）
   • k为奇数：从上往下遍历（行索引递增，列索引递减）
3. 确定每条对角线的起始点：
   • 当k < min(m, n)时，起始点在矩阵边缘
   • 当k ≥ min(m, n)时，起始点向矩阵内部移动

代码实现

class Solution {public int[] findDiagonalOrder(int[][] mat) {if (mat == null || mat.length == 0) return new int[0];int m = mat.length;int n = mat[0].length;int[] result = new int[m * n];int index = 0;// 遍历所有对角线（k = i + j）for (int k = 0; k < m + n - 1; k++) {if (k % 2 == 0) { // 偶数对角线：从下往上// 确定起始点int i = Math.min(k, m - 1);int j = k - i;// 沿对角线向上遍历while (i >= 0 && j < n) {result[index++] = mat[i][j];i--;j++;}} else { // 奇数对角线：从上往下// 确定起始点int j = Math.min(k, n - 1);int i = k - j;// 沿对角线向下遍历while (j >= 0 && i < m) {result[index++] = mat[i][j];i++;j--;}}}return result;}
}

算法解析

关键步骤详解

边界处理技巧

1. 起始点确定：
   • 偶数对角线：i = min(k, m-1), j = k - i
   • 奇数对角线：j = min(k, n-1), i = k - j
2. 遍历终止条件：
   • 当行索引或列索引超出矩阵边界时停止
3. 方向切换：
   • 利用k的奇偶性自然切换方向

复杂度分析

指标	值	说明
时间复杂度	O(m*n)	每个元素访问一次
空间复杂度	O(1)	除结果数组外无额外空间
遍历效率	100%	最优解

拓展思考

变体问题

1. Z字形打印矩阵
2. 螺旋矩阵遍历
3. 对角线求和问题

总结

对角线遍历问题展示了如何通过观察矩阵的数学特性（行索引+列索引=常数）来设计高效算法。关键在于：

1. 识别对角线遍历的数学规律
2. 巧妙处理遍历方向的交替变化
3. 精确控制边界条件