【Luogu】P4317 花神的数论题 (数位DP)

P4317 花神的数论题 - 洛谷

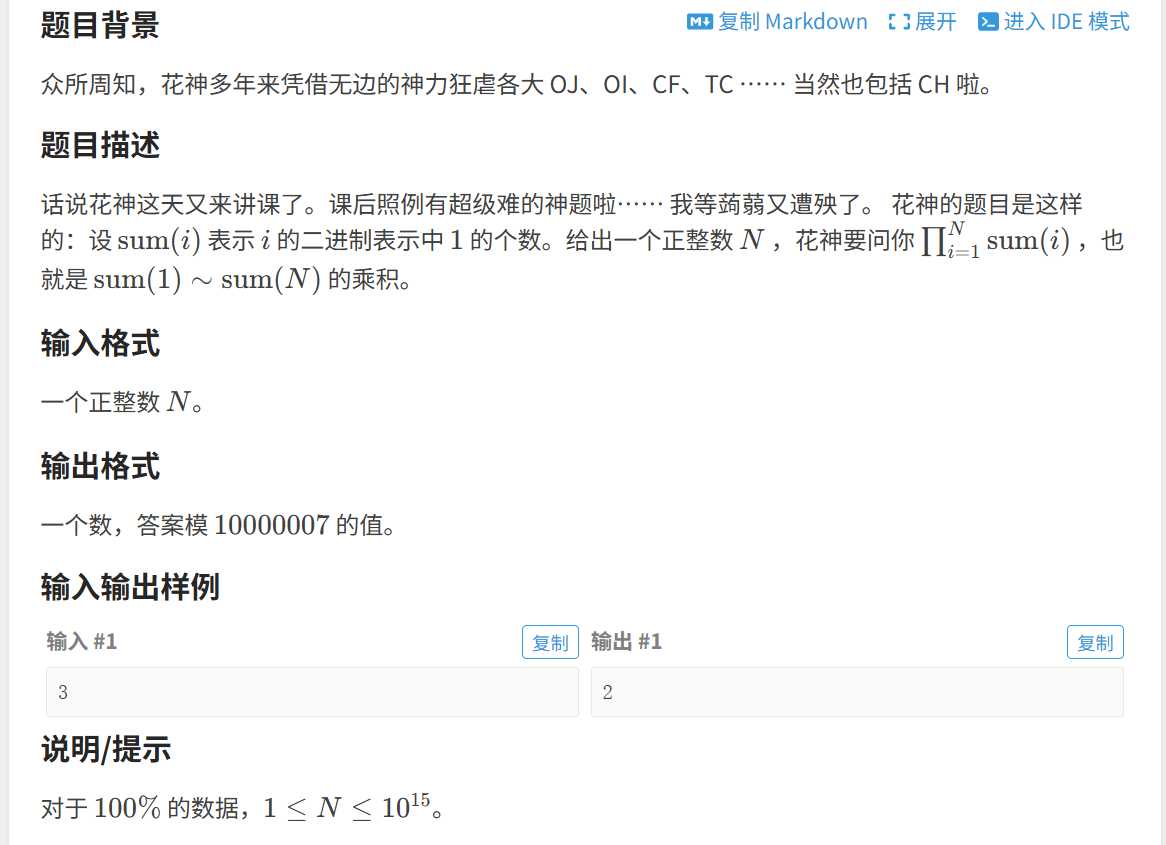
题目：

思路：

数位DP

本题让我们求 sum(i) 的乘积，其中 i 属于 1 ~ N，sum(i) 代表二进制中 i 的 1 的个数

那么转化题意，我们数位DP是计算符合某些特征的数字的个数，那么本题中我们也是将答案拆分一个一个求

具体的，我们这里的特征可以定义为在二进制下含有 k 个 1 的数的个数，那么我们只需要求出所有可能 k 的个数即可，然后用个快速幂乘起来就是答案，为什么呢？因为 sum(i) 其实算的就是 1 的数量，多个同样的 sum 不就刚好符合快速幂吗，而这里我们就是枚举 sum(i) 来快速得到答案

所以考虑记忆化搜索，我们定义 dp[i][k][j] 为 处理了 i 位，且当前枚举的 sum(i) 为 k，之前已经有过 j 个 1 的结果

那么考虑 dfs 状态，我们既然要知道二进制下的 1 的数量，不妨考虑直接枚举二进制形式下的数，既能快速计算 1，也能枚举到所有情况

而对于参数部分我们只需要多一个 sum 用于储存之前有过多少个 1 即可，其余都是板子

具体实现看代码，难点在于想到直接枚举二进制，以及分解为求固定 sum(i)

代码：

#include <bits/stdc++.h>
using namespace std;
#define int long long
#define yes cout << "YES\n"
#define no cout << "NO\n"
#define Sunny 0
mt19937 rnd(chrono::steady_clock::now().time_since_epoch().count());const int MOD = 10000007;
int a[64], len = 0;
//i 位 1 数量为 j
int dp[64][64][64];
int nowchose;
int dfs(int now,int lim,int sum)
{if(!now) return sum==nowchose;if(!lim && dp[now][nowchose][sum] != -1) return dp[now][nowchose][sum];int mx = lim ? a[now] : 1;int res = 0;for(int i = 0;i <= mx;i++){res += dfs(now-1,lim && i == mx,sum + (i == 1));}if(!lim) dp[now][nowchose][sum] = res;return res;
}int qp(int a,int b)
{int res = 1;a %= MOD;while (b){if(b & 1) res = res * a % MOD;a = a*a % MOD;b >>= 1;}return res;
}void solve()
{int x;cin >> x;while (x)a[++len] = x & 1, x>>=1;memset(dp,-1,sizeof dp);int ans = 1;//枚举多少个 1for (int i = 1; i <= len; i++){nowchose = i;ans = ans * qp(i,dfs(len,1,0)) % MOD;}cout << ans << endl;
}signed main()
{ios::sync_with_stdio(false);cin.tie(nullptr);int t = 1;while (t--){solve();}return Sunny;
}