C++ AOV 拓扑排序

提示：文章写完后，目录可以自动生成，如何生成可参考右边的帮助文档

---

前言

本文主要记录AOV算法的实现。

图论中将图分为有向图与无向图，同时还可以根据是否有回路分为有环图与无环图。

软考中级经常会考到若干关于工期的安排问题：

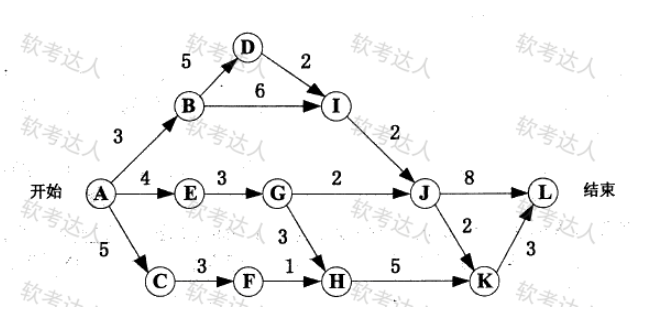
上面的图就是一个有向无环图（DAG）

---

一、AOV是什么？

AOV首先是一个DAG，然后在这个图中，顶点用来表示活动（Active on vertices）并利用边u->v来表示u是v的先决条件（v依赖u），同时具有传递性（u是v的先决，v是w的先决，那么u也算是w的先决）。正是因为这个依赖传递，如果存在u->v v->w w->u，就会推出u->u也就是u依赖他自己，这个是不行的。学术化一点就是反自反性，这也是为什么AOV必须是一个有向无环图DAG。

二、拓扑排序

基于AOV网格，可以完成拓扑排序，将AOV网格中的节点存到一个列表中，保证在AOV中u->v，在列表中u会存放在v的前面（不一定是挨着的）

算法思路：

1.遍历AOV网格，寻找所有入度为0的节点，并放入一个容器中
2.从容器中拿出一个入度为0的节点，将所有与该节点相邻的节点的边删除（物理层面上也可以不删除），并给他们的入度减小1（这个必须要做）
3.同时判断“删除”边后，是否有新的节点入度为0,如果有就放入到容器中
4.循环上面2 3 的过程，直到容器没有节点。此时可以判断如果还有节点的入度不为0，就代表当前图有环。反之则代表拓扑排序成功结束

三、代码实现

#include <iostream>
#include <stack>
using std::cin;
using std::cout;
using std::stack;const int MAXN = 100;// 边节点
struct ArcNode{int no;ArcNode *next;ArcNode(){}ArcNode(int no){this->no = no;next = nullptr; }
};//顶点节点
struct VNode
{int no;// 当前节点的入度int indegree;ArcNode* firstArc;VNode(){no = -1;indegree = 0;firstArc = nullptr;}VNode(int no, int indegree, ArcNode* firstArc){this->no = no;this->indegree = indegree;this->firstArc = firstArc;}// 头插法将边界点插入到顶点节点下面void insert(ArcNode* node){node->next = this->firstArc;this->firstArc = node;}~VNode(){}
};//领接表
struct ADGList
{VNode v[MAXN];int vexnum,arcnum;ADGList(){for(int i = 0; i < MAXN; i ++){v[i].no = i;}}void print(){for(int i = 0; i < vexnum; i ++){ArcNode* p = v[i].firstArc;while(p != nullptr){cout << p->no << " -->  ";p = p->next;}cout << "NULL\n";}}
};void createAGDList(ADGList& adglist){int vnum,arcnum; // 顶点数  边数int u,v; // 用于表示每一条边的起点终点cin >> vnum >> arcnum;adglist.vexnum = vnum;adglist.arcnum = arcnum;for(int i = 0; i < arcnum; i ++){cin >> u >> v;adglist.v[u].insert(new ArcNode(v));adglist.v[v].indegree ++;}
}void topoSort(ADGList& adglist){std::deque<int> zero_ind_q,ans_q;// 将领接表中入度为0的顶点节点压入到栈中int n = adglist.vexnum;for(int i = 0; i < n; i ++){if(adglist.v[i].indegree == 0){zero_ind_q.push_back(i);}}while(!zero_ind_q.empty()){int zero_ind_node = zero_ind_q.front();zero_ind_q.pop_front();ans_q.push_back(zero_ind_node);ArcNode* p = adglist.v[zero_ind_node].firstArc;while(p != nullptr){adglist.v[p->no].indegree --;if(adglist.v[p->no].indegree == 0){zero_ind_q.push_back(p->no);}p = p->next;} // cout << "zero_ind_q.size is" << zero_ind_q.size() << "\n";   }cout << "topoSort done!\n";while(!ans_q.empty()){int front = ans_q.front();ans_q.pop_front();cout << front << " ";}}int main(int argc, const char** argv) {ADGList adglist;createAGDList(adglist);adglist.print();topoSort(adglist);return 0;
}