当前位置：首页 > news >正文

遇到的数学知识补充

news 2025/8/24 8:19:09

iid(独立同分布)

同分布：所有数据点都来自同一个“数据生成机制”，遵循完全相同的概率规则。比如，它们都来自同一个概率分布（如正态分布、均匀分布等），具有相同的均值、方差等参数。

独立：任何一个数据点的出现，都不会影响另一个数据点出现的概率。

似然函数(MLE)

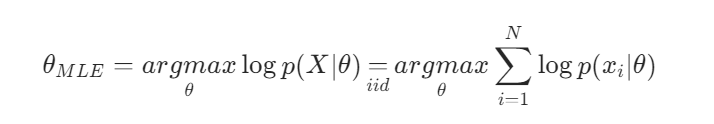
建立在iid的基础之上。

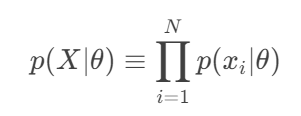
X：代表我们观测到的整个数据集。

θ：代表模型未知的参数。在测量身高的例子中，θ 可能是身高的平均值 μ 和标准差 σ。

p(X∣θ)：这是在给定参数 θ 的某个具体值时，观测到整个数据集 X 的概率。这个函数被称为关于参数 θ 的似然函数。

p( $x_{i}$ ∣θ)： 这是在给定参数 θ 时，观测到单个数据点 $x_{i}$ 的概率。

贝叶斯定理

θ：我们想要估计的未知参数。

X：我们观测到的数据集。

p(θ)：这是先验分布（Prior Distribution）。它代表我们在看到任何数据 X 之前，对参数 θ 可能取值的初始信念或知识。这是一个概率分布。

p(X∣θ)：这是似然函数（Likelihood Function）。

p(θ∣X)：这是后验分布（Posterior Distribution）。它代表在已经观测到数据 X 之后，我们对参数 θ 的更新后的信念。这是我们最终想要得到的结果。

p(X)：称为证据（Evidence）或边际似然，（在概率论中，“边际化”是指通过对一个变量进行积分，将其从联合分布中“消除”掉，从而得到另一个变量的分布。）是一个“归一化常数”，它的唯一作用就是调整等式右边分子的大小，确保最终计算出的后验概率 p(θ∣X) 是一个总和为1的、有效的概率分布。

分子 p(θ∣X) * p(θ)：就像是披萨上属于“参数值为 θ”的那一块的大小。不同的 θ 对应不同大小的披萨块。
分母 p(X)：就是整个披萨的大小。
后验概率 p(θ∣X)：就是“参数值为 θ”的那一块披萨占整个披萨的比例。

最大后验概率估计(MAP)

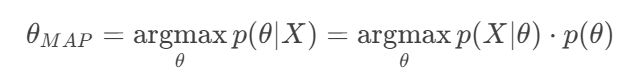
1. 目标是什么？

目标是找到一个具体的、最可能的参数值 θ，而不是完整的后验分布p(θ∣X)。
argmax 操作就是找到使函数值最大的那个输入（θ 的值）。

2. 为什么可以忽略分母p(X)？

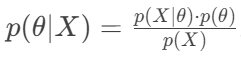
在比较不同 θ 对应的 p(θ∣X) 的大小时，p(X) 就像一个公共的缩放因子。它不会改变哪个 θ 能使分子 p(X∣θ)⋅p(θ) 达到最大。

MLE与MAP的区别

MLE：

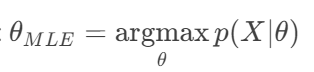
只关心什么参数最可能产生观测到的数据。

MAP：

在 MLE 的基础上，加上了先验信念 p(θ) 的约束。
它寻找的是：在考虑到我们已有知识（先验） 的情况下，什么参数最可能产生观测到的数据。
先验p(θ) 在这里起到了正则化（Regularization） 的作用，防止参数跑到我们根据常识认为不合理的区域，有助于避免过拟合。

贝叶斯预测 (Bayesian Prediction)

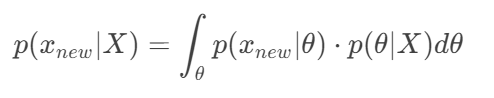
1. 目标是什么？

在得到参数的后验分布p(θ∣X) 之后，我们最终的目的不是参数本身，而是预测新的、未见过的数据 $x_{new}$ 。
我们想要的是预测分布p( $x_{new}$ ∣X)，即在已有数据 X 的条件下，新数据点出现的概率。

2. 如何理解这个积分？

这个公式是贝叶斯思想的精髓：不考虑某个具体的参数，而是考虑所有可能的参数，用它们的后验概率作为权重，求平均预测。

p( $x_{new}$ ∣θ)：这是模型。如果参数确定是 θ，那么新数据点的预测概率是多少。
p(θ∣X)：这是后验分布。它告诉我们，在看到数据 X 后，我们有多相信参数是 θ。
积分 $\int_\theta...d\theta$ ：这个积分遍历了所有可能的参数值 θ。对于每一个 θ ，我们计算它给出的预测 p( $x_{new}$ ∣θ)，然后用我们相信这个 θ 的程度p(θ∣X) 作为权重，最后对所有可能的预测进行加权平均。

3.推导

第一步：引入参数 $\theta$

$p(x_{new}|X)=\int_\theta p(x_{new},\theta|X)d\theta$

这个公式的意思是：“在给定 $X$ 时， $x_{new}$ 发生的概率” 等于 “在给定 $X$ 时， $x_{new}$ 和每一个可能的 $\theta$ 同时发生的概率” 对所有 $\theta$ 求和（积分）。

第二步：应用条件概率公式

对积分号内的联合概率 $p(x_{new},\theta|X)$ 应用条件概率公式 $P(A,B)=P(A|B)\cdot P(B)$ 。这里，将 $A$ 视为 $x_{new}$ ,将 $B$ 视为 $\theta$ ,条件都是 $X:$

$p(x_{new},\theta|X)=p(x_{new}|\theta,X)\cdot p{(\theta|X)}$

将其代入第一步的等式中：

$p(x_{new}|X)=\int_\theta p(x_{new}|\theta,X)\cdot p(\theta|X)d\theta$

第三步：应用条件独立假设

这是一个关键步骤。我们的模型通常有一个重要假设：在已知生成参数 $\theta$ 的情况下，所有数据点(包括已有的数据 $X$ 和新的数据 $x_{new}$ )都是相互独立的。也就是说，一旦 $\theta$ 确定， $x_{new}$ 的生成不再依赖于已有的数据 $X$ 。

用数学公式表达就是这个条件独立关系：

$p(x_{new}|\theta,X)=p(x_{new}|\theta)$

这个假设是成立的，因为根据模型，数据都是由同一个参数 $\theta$ 独立同分布 (i.i.d.)地生成的。知道 $X$ 并不能给我们关于 $x_{new}$ 的更多信息，因为所有信息都已经蕴含在 $\theta$ 中了。

将这个关系代入上式：

$p(x_{new}|X)=\int_\theta p(x_{new}|\theta)\cdot p(\theta|X)d\theta$

期望值（Expected Value）和均值（Mean）

均值是“已经发生”的数据的平均值，而期望值是“未来可能发生”的平均值。

1. 均值 (Mean) — 描述“过去”或“样本”

它是什么：均值（通常记作 $\bar{x}$ ）是一个描述性统计量。它针对的是你已经收集到的、有限的、具体的数据集（一个“样本”）。
如何计算：你有一个装着数字的袋子，你把手伸进去，把所有数字拿出来，加起来，再除以数字的个数。得到的就是这“一把”数字的均值。
本质：对已知观测值的算术平均。
例子：
- 你抛一枚硬币10次，结果是4次正面，6次反面。正面朝上的比例（均值） 是 4/10=0.4。
- 你统计了班上50个同学的身高，加起来除以50，得到平均身高是172cm。

2. 期望值 (Expected Value) — 描述“未来”或“总体”

它是什么：期望值（通常记作 $E[X]$ 或 $\mathrm{u}$ ）是一个概率论概念。它针对的是一个随机变量的理论上的、无限次的长期平均结果（整个“总体”）。
如何计算：它不是对已有数据做平均，而是对随机变量所有可能的结果按其发生的概率进行加权平均。
- 公式： $E[X]=\sum_\text{all x }x\cdot P(X=x)$ （对于离散变量）
- 公式： $E[X]=\int_{-\infty}^{\infty}x\cdot f(x)dx$ （对于连续变量，f(x)是概率密度函数PDF）
- 常数可以提到期望外面：对于任意常数 c，有 $\mathbb{E}[c]=c$ 。
- 和的期望等于期望的和： $\mathbb{E}[X+Y]=\mathbb{E}[X]+\mathbb{E}[Y]$ 。
- 常数系数可以提到期望外面： $\mathbb{E}[cX]=c\mathbb{E}[X]$ 。
本质：理论上“应该”出现的平均结果，是随机变量概率分布的中心。
例子：
- 在抛一枚均匀硬币之前，我们知道正面朝上的概率是0.5。那么，抛硬币结果的期望值就是（1×0.5)+(0×0.5)=0.5。这意味着，如果我们能抛这枚硬币无限多次，正面朝上的比例将会是0.5。
- 掷一个公平骰子，点数的期望值是 $(1\times\frac{1}{6})+(2\times\frac{1}{6})+...+(6\times\frac{1}{6})=3.5$ 。这意味着，长期来看，平均每次掷出的点数是3.5。

方差（Variance）

方差是统计学和概率论中最核心的概念之一，它衡量的是随机变量或一组数据与其平均值的平均偏离程度（分散程度）。简单说，方差越大，数据点越分散；方差越小，数据点越集中在平均值附近。

1. 数学定义

方差在数学上定义为随机变量与其期望值（均值）之差的平方的期望值。

$\mathrm{Var}(X)=E\left[(X-\mu)^2\right]$

其中：

E[...]表示期望值（Expected Value），可以理解为一种加权平均。
$\mu$ 是随机变量X的均值(期望值),即 $\mu=E[X]$ 。
$X-\mu$ 是每个数据点与均值的偏差（Deviation）。
$(X-\mu)^2$ 是偏差的平方。这里平方是关键，它有两个目的：
1. 消除正负号：防止正偏差和负偏差相互抵消。
2. 放大远离均值的点：距离均值越远的点，平方后对方差的贡献越大。

2. 计算公式（对于数据集）

对于一份包含 $N$ 个数据点的有限数据集 $\{x_1, x_2, ..., x_N\}$ , 其方差的计算公式为:
总体方差（Population Variance）：
（当你的数据集包含了所有可能的数据时使用）

$\sigma^2=\frac{1}{N}\sum_{i=1}^N(x_i-\mu)^2$

样本方差（Sample Variance）：

（当你的数据集只是一个更大总体的“样本”时使用，用 $s^2$ 表示）

$s^2=\frac{1}{N-1}\sum_{i=1}^N(x_i-\bar{x})^2$

其中：

$\bar{x}$ 是样本均值 $(\bar{x}=\frac{1}{N}\sum_{i=1}^Nx_i)$ 。
分母使用 N−1而不是N，这是为了进行无偏估计（Bessel's Correction），使得样本方差更接近总体方差的真实值。

3. 为什么定义要“平方”？

假设有5个数据点：[3, 5, 7, 9, 11]。均值μ=7。

数据点 $x_{i}$	偏差 $(x_i-\mu)$	偏差的平方 $(x_i-\mu)^2$
3	-4	16
5	-2	4
7	0	0
9	+2	4
11	+4	16
和	0 (抵消)	40

如果直接对偏差 $(x_i-\mu)$ 求平均，正负会相互抵消，结果为0。这无法衡量分散程度。
对偏差平方后再求平均，得到了40 / 5 = 8。这个值（方差）成功地量化了数据的波动性。

所以，“平方”是为了避免正负抵消，并更突出远离均值的点。

标准差（Standard Deviation）

方差有一个缺点：它的单位是原始数据单位的平方。

例如，如果数据单位是“米”，方差单位就是“平方米”，这有时不直观。

为了解决这个问题，我们引入标准差（Standard Deviation），即方差的平方根：

$\sigma=\sqrt{\sigma^2}$

标准差和原始数据有相同的单位，因此更常被用于描述数据的分散程度。

协方差（Covariance）

协方差是方差概念的延伸，它衡量的是两个随机变量一起变化的趋势和方向。

1. 核心直观理解

方差衡量的是一个变量自身如何变化（分散程度）。
协方差衡量的是两个变量之间的关系：

正协方差：当一个变量大于其均值时，另一个变量也倾向于大于其均值。两者变化方向相同。
- 例如：身高和体重通常有正协方差。
负协方差：当一个变量大于其均值时，另一个变量却倾向于小于其均值。两者变化方向相反。
- 例如：每天玩游戏的时间和学习成绩可能具有负协方差。
协方差接近零：两个变量的变化似乎没有线性关系（注意：可能还存在其他非线性关系）。

2. 数学定义

对于两个随机变量 $X$ 和 $Y$ ，其协方差 $\operatorname{Cov}(X, Y)$ 或 $\sigma_{xy}$ 定义为它们各自与均值偏差的乘积的期望值：

$\mathrm{Cov}(X,Y)=E\left[(X-\mu_x)(Y-\mu_y)\right]$

其中：

$E[...]$ 是期望值算子。
$\mu_x=E[X]$ , 是 $X$ 的均值。
$\mu_y=E[Y]$ , 是 $Y$ 的均值。
$(X-\mu_x)$ 是 $X$ 的偏差。
$(Y-\mu_y)$ 是 $Y$ 的偏差。

这个公式的精妙之处在于：

如果两个偏差同号（都是正或都是负），它们的乘积为正，对协方差贡献一个正值。
如果两个偏差异号（一正一负），它们的乘积为负，对协方差贡献一个负值。
对所有这样的组合求平均（期望），就得到了衡量两者协同变化程度的协方差。

3. 计算公式（对于数据集）

对于一份包含 $N$ 个成对观测值的数据集 $\{(x_{1},y_{1}),(x_{2},y_{2}),...,(x_{N},y_{N})\}$ :

总体协方差：

$\sigma_{xy}=\frac{1}{N}\sum_{i=1}^{N}(x_i-\mu_x)(y_i-\mu_y)$

样本协方差（更常用）：

$s_{xy}=\frac{1}{N-1}\sum_{i=1}^N(x_i-\bar{x})(y_i-\bar{y})$

其中 $\overline{x}$ 和 $\overline{y}$ 是样本均值。分母使用 N−1 是为了进行无偏估计。

4. 一个重要特例：变量与自身的协方差

协方差有一个非常重要的性质：
一个变量与其自身的协方差，就是它的方差。

$\mathrm{Cov}(X,X)=E[(X-\mu_x)(X-\mu_x)]=E[(X-\mu_x)^2]=\mathrm{Var}(X)$

5. 协方差的局限性

协方差的值的大小没有上限，它依赖于变量本身的尺度（scale）。这意味着：

我们很难从协方差的数值本身（比如 50 或 -100）直接判断两个变量关系的强弱，只能判断方向（正相关或负相关）。
比较不同组变量之间的相关性强度会很困难。

举个例子：

如果我们将身高的单位从“米”改成“厘米”（数值放大100倍），协方差的值会急剧增大（放大10,000倍），但两个变量之间的实际关系强度并没有改变。

为了解决这个局限性，我们引入了相关系数。

总结：

协方差：定量描述两个变量如何共同变化。
- > 0：正相关
- < 0：负相关
- = 0：无线性相关
它的值是有单位的，其大小受变量自身尺度影响。
它是构建协方差矩阵和计算相关系数的基础。

特性	协方差 (Covariance)	相关系数 (Correlation)
衡量对象	两个变量的协同变化	两个变量的线性关系强度和方向
取值范围	(−∞,+∞)(−∞,+∞)	[−1,1][−1,1]
消除尺度	否	是
解释性	弱（数值大小无明确意义）	强（-1：完全负相关；1：完全正相关）

估计量的偏差（Bias）

偏差衡量的是：你所有射击的平均落点，离靶心有多远。

无偏：平均落点正好是靶心。虽然每一箭不一定都命中，但没有系统性的瞄准错误。
有偏：平均落点偏离了靶心。存在系统性的、一贯的瞄准错误（要么总是偏左，要么总是偏右，要么总是偏上/下）。

数学定义：

$\theta$ 是我们想要估计的未知参数的真值。
$\hat{\theta}$ 是我们根据样本数据计算出的估计量。

$\mathrm{Bias}(\hat{\theta})=\mathbb{E}[\hat{\theta}]-\theta$

其中 $\operatorname{E}[\hat{\theta}]$ 是估计量 $\hat{\theta}$ 的期望值（即反复抽样无数次，计算出的所有估计值的平均值）。

如果 $\mathbb{E}[\hat{\theta}]=\theta$ ，则 $\mathrm{Bias}(\hat{\theta})=0$ ，我们称 $\hat{\theta}$ 为 无偏估计量（Unbiased Estimator）。
如果 $\mathbb{E}[\hat{\theta}]\neq\theta$ ，则 $\mathrm{Bias}(\hat{\theta})\neq0$ ，我们称 $\hat{\theta}$ 为 有偏估计量（Biased Estimator）。

方差和偏差在机器学习上的解释

1. 偏差 (Bias) - “系统性错误”

是什么：模型为了简化学习任务而做出的错误假设，导致它无法捕捉数据中的真实 underlying pattern（潜在规律）。
高偏差的表现：无论在什么样的训练数据上学习，模型都会犯同样类型的错误。它在训练集上的表现就很差。
起因：模型太简单（例如，用一条直线去拟合一个弯曲的数据 pattern）。
结果：欠拟合 (Underfitting)。

2. 方差 (Variance) - “对波动的敏感性”

是什么：模型对训练数据中的随机噪声（而非真实规律）的过度学习程度。
高方差的表现：如果换一批训练数据，模型学出的结果会发生剧烈变化。它在训练集上表现极好，但在没见过的数据上表现很差。
起因：模型太复杂（例如，用一个100次的多项式去拟合一个由10个数据点生成的 pattern）。
结果：过拟合 (Overfitting)。

高斯分布

一维情况 MLE

$\theta=(\mu,\Sigma)=(\mu,\sigma^2)$

$\theta_{\mathrm{MLE}}=\underset{\theta}{\operatorname*{\operatorname*{argmax}}}\log p(X|\theta)=\underset{\theta}{\operatorname*{\operatorname*{argmax}}}\sum_{i=1}^N\log p(x_i|\theta)$

一元高斯分布

$p(x|\mu,\sigma)=\frac{1}{(2\pi)^{1/2}\sigma}\exp\left(-\frac{1}{2}\frac{(x-\mu)^2}{\sigma^2}\right)=\frac{1}{\sqrt{2\pi}\sigma}\exp\left(-\frac{(x-\mu)^2}{2\sigma^2}\right)$

当维度 p=1时，这个复杂的多元公式就退化为我们熟悉的一元高斯分布公式：

$x,\mu$ 是标量。
协方差矩阵 $\Sigma$ 退化方差 $\sigma^2$ （一个标量）。
$|\Sigma|^{1/2}=\sigma$ 。
$\Sigma^{-1}=1/\sigma^2$ 。
$(x-\mu)^T\Sigma^{-1}(x-\mu)=(x-\mu)^2/\sigma^2$

带入 MLE 中我们考虑一维的情况

$\log p(X|\theta)=\sum_{i=1}^N\log p(x_i|\theta)=\sum_{i=1}^N\log\frac{1}{\sqrt{2\pi}\sigma}\exp(-(x_i-\mu)^2/2\sigma^2)$

1. 目标是什么？

我们的目标是：找到一组参数 $\theta$ ，使得我们观测到的数据集 $X$ 出现的可能性最大。

对于一维高斯分布，参数 $\theta$ 就是均值 $\mu$ 和方差 $\sigma^{2}$ ，即 $\theta=(\mu,\sigma^2)$ 。

2. 公式分解

似然函数的对数：

$\log p(X|\theta)=\sum_{i=1}^N\log p(x_i|\theta)$

p(X∣θ)：在给定参数 θ 下，出现整个数据集 X 的联合概率密度（即似然函数）。
由于我们假设数据是独立同分布 (i.i.d.) 的，联合概率密度等于每个数据点概率密度的乘积： $p(X|\theta)=\prod_{i=1}^Np(x_i|\theta)$ 。
直接最大化这个乘积在数学上很麻烦（容易下溢，且求导复杂），所以我們取其对数，将连乘变为求和： $\log p(X|\theta)=\sum_{i=1}^N\log p(x_i|\theta)$ 。
因为对数函数是单调递增的，最大化 $\log p(X|\theta)$ 等价于最大化 p(X∣θ)。这个求和后的函数称为对数似然函数（Log-Likelihood）。

代入高斯分布的PDF：

$\sum_{i=1}^N\log p(x_i|\theta)=\sum_{i=1}^N\log\left[\frac{1}{\sqrt{2\pi}\sigma}\exp(-(x_i-\mu)^2/2\sigma^2)\right]$

对于每一个数据点 $x_{i}$ ，它在这个高斯分布下的概率密度是

$p(x_i|\mu,\sigma^2)=\frac{1}{\sqrt{2\pi}\sigma}\exp\left(-\frac{(x_i-\mu)^2}{2\sigma^2}\right)$

3. 为什么要这样做？

写下这个带具体分布形式的对数似然函数，是为了后续的求导和最大化。

利用对数的性质 $(\log(ab)=\log a+\log b,\log e^a=a)$ 将这个复杂的表达式展开和简化。

$\begin{aligned}\log p(X|\theta)&=\sum_{i=1}^N\log\left[\frac{1}{\sqrt{2\pi}\sigma}\exp\left(-\frac{(x_i-\mu)^2}{2\sigma^2}\right)\right]\\&=\sum_{i=1}^N\left[\log\left(\frac{1}{\sqrt{2\pi}\sigma}\right)+\log\left(\exp\left(-\frac{(x_i-\mu)^2}{2\sigma^2}\right)\right)\right]\\&=\sum_{i=1}^N\left[-\log(\sqrt{2\pi})-\log(\sigma)-\frac{(x_i-\mu)^2}{2\sigma^2}\right]\\&=-\frac{N}{2}\log(2\pi)-N\log(\sigma)-\frac{1}{2\sigma^2}\sum_{i=1}^N(x_i-\mu)^2\end{aligned}$

识别常数项：

$-\log(\sqrt{2\pi})$ ：这是一个常数，它的值不依赖于需要优化的参数 μ或 σ。
$-\log(\sigma)$ ：这项依赖于参数 σ，但不依赖于参数 μ。在我们专门优化 μ 时，可以把这项看作相对于 μ 的常数。
$-\frac{(x_i-\mu)^2}{2\sigma^2}$ ：这项同时依赖于数据 $x_{i}$ 、参数 μ 和参数 σ。

构建只与 μ相关的目标函数：

$\mu_{MLE}=\underset{\mu}{\operatorname*{\operatorname*{argmax}}}\log p(X|\theta)$

等价于：

$\mu_{MLE}=\underset{\mu}{\operatorname*{\operatorname*{argmax}}}\left[{\operatorname*{\operatorname*{Constant}}}-\frac{1}{2\sigma^2}\sum_{i=1}^N(x_i-\mu)^2\right]$

因为 Constant和系数 $\frac{1}{2\sigma^2}$ 都是正的常数（方差 $\sigma^{2}>0$ ），所以：

最大化 $\left[\mathrm{Constant}-\frac{1}{2\sigma^2}\sum(x_i-\mu)^2\right]$
等价于最小化 $\frac{1}{2\sigma^2}\sum(x_i-\mu)^2$ （因为减去一个东西要最大，就等于让这个东西本身最小）
等价于最小化 $\sum(x_i-\mu)^2$ （因为乘以正常数 $\frac{1}{2\sigma^2}$ 不影响最小值点的位置）

得到：

$\mu_{MLE}=\underset{\mu}{\operatorname*{\operatorname*{\mathrm{argmax}}}}\log p(X|\theta)=\underset{\mu}{\operatorname*{\operatorname*{\mathrm{argmin}}}}\sum_{i=1}^N(x_i-\mu)^2$

构建只与 $\sigma$ 相关的目标函数：

$\sigma_{MLE}=\underset{\sigma}{\operatorname*{\operatorname*{argmax}}}\log p(X|\theta)$

由下列式子：

$-\frac{N}{2}\log(2\pi)-N\log(\sigma)-\frac{1}{2\sigma^{2}}\sum_{i=1}^{N}(x_{i}-\mu)^{2}$

得到：

$\begin{aligned}\sigma_{MLE}=argmax\log p(X|\theta)&=argmax\sum_{i=1}^N[-\log\sigma-\frac{1}{2\sigma^2}(x_i-\mu)^2]\\&=argmin\sum_{i=1}^N[\log\sigma+\frac{1}{2\sigma^2}(x_i-\mu)^2]\end{aligned}$

分别对参数求导并令导数为零：

对参数 μ求偏导，令 $\frac{\partial\log p(X|\theta)}{\partial\mu}=0$ ，可以解出 μ的最大似然估计值。
对参数 $\sigma^2$ 求偏导，令 $\frac{\partial\log p(X|\theta)}{\partial\sigma^2}=0$ ，可以解出 $\sigma^2$ 的最大似然估计值。

对目标函数 J(μ)关于 μ求导：

$\begin{aligned}J(\mu)&=\sum_{i=1}^N(x_i-\mu)^2\\\frac{\partial J(\mu)}{\partial\mu}&=\frac{\partial}{\partial\mu}\left[\sum_{i=1}^N(x_i-\mu)^2\right]\end{aligned}$

将求导符号移入求和符号内（因为导数是线性算子）：

$\frac{\partial J(\mu)}{\partial\mu}=\sum_{i=1}^N\frac{\partial}{\partial\mu}(x_i-\mu)^2$

对求和内的每一项求导：

对于每一项 $(x_i-\mu)^2$ ，我们可以将其看作一个复合函数。令 $u=(x_i-\mu)$ ，则该项为 $u^2$ 。
根据链式法则：

$\frac{\partial}{\partial\mu}(u^2)=\frac{\partial(u^2)}{\partial u}\cdot\frac{\partial u}{\partial\mu}=2u\cdot(-1)=-2(x_i-\mu)$

$\frac{\partial J(\mu)}{\partial\mu}=\sum_{i=1}^N\left[-2(x_i-\mu)\right]=-2\sum_{i=1}^N(x_i-\mu)$

令导数等于零，以找到极小值点：

$\frac{\partial J(\mu)}{\partial\mu}=0$

$-2\sum_{i=1}^N(x_i-\mu)=0$

对函数关于 $\sigma$ 求导：

$\frac{\partial}{\partial\sigma}\log p(X|\mu,\sigma^2)=\frac{\partial}{\partial\sigma}\left[-\frac{N}{2}\log(2\pi)-N\log(\sigma)-\frac{1}{2\sigma^2}S\right]$

其中， $S=\sum_{i=1}^N(x_i-\mu)^2$ 是一个常数（在求 σ的极值时，μ和 S都被视为已知或已估计）。

$\frac{\partial\log p}{\partial\sigma}=0-N\cdot\frac{1}{\sigma}+S\sigma^{-3}=-\frac{N}{\sigma}+\frac{S}{\sigma^3}$

$\begin{gathered}-\frac{N}{\sigma}+\frac{S}{\sigma^3}=0\\\frac{S}{\sigma^3}=\frac{N}{\sigma}\end{gathered}$

$S=N\sigma^2$

求出解析解：

$\mu_{MLE}=\frac{1}{N}\sum_{i=1}^Nx_i$

$\sigma_{MLE}^2=\frac{1}{N}\sum_{i=1}^N(x_i-\mu_{MLE})^2$

求出MLE:

首先假设真实值为 $\mu$ ，求 $\mu$ 的MLE，然后利用这个结果求 $\sigma_{MLE}$ ，因此可以预期的是对数据集求期望时 $\mathbb{E}_{\mathcal{D}}[\mu_{MLE}]$ 是无偏差的：

$\mathbb{E}_D[\mu_{MLE}]=\mathbb{E}_D\left[\frac{1}{N}\sum_{i=1}^Nx_i\right]\\=\frac{1}{N}\sum_{i=1}^N\mathbb{E}_D[x_i]\\=\frac{1}{N}\sum_{i=1}^N\mu=\frac{1}{N}(N\mu)=\mu$

第一个等号：将 $\mu_{MLE}$ 的定义代入。
第二个等号：期望算子 $E$ 是线性的，可以移到求和号里面。这是最关键的一步。
第三个等号：因为每个数据点 $x_{i}$ 都是从均值为 $\mu$ 的分布中独立抽取的，所以 $\mathbb{E}_D[x_i]=\mu$ 。
结果： $\mathbb{E}_D[\mu_{MLE}]=\mu$ 。这意味着，尽管某一次抽样计算出的 $\mu_{MLE}$ 可能不等于真实的 $\mu$ ，但如果你无数次地重复“抽样-计算”这个过程，这些 $\mu_{MLE}$ 的平均值会无限接近真实的 $\mu$ 。因此， $\mu_{MLE}$ 是真实均值 $\mu$ 的一个无偏估计。

对 $\sigma_{MLE}$ 求期望的时候由于使用了单个数据集的 $\mu_{MLE}$ ，因此对所有数据集求期望的时候我们会发现 $\sigma_{MLE}$ 是有偏的：

$\begin{aligned}\mathbb{E}_D[\sigma_{MLE}^2]&=\mathbb{E}_{\mathcal{D}}[\frac{1}{N}\sum_{i=1}^N(x_i-\mu_{MLE})^2]=\mathbb{E}_{\mathcal{D}}[\frac{1}{N}\sum_{i=1}^N(x_i^2-2x_i\mu_{MLE}+\mu_{MLE}^2)\\&=\mathbb{E}_{\mathcal{D}}[\frac{1}{N}\sum_{i=1}^Nx_i^2-\mu_{MLE}^2]=\mathbb{E}_{\mathcal{D}}[\frac{1}{N}\sum_{i=1}^Nx_i^2-\mu^2+\mu^2-\mu_{MLE}^2]\\&=\mathbb{E}_\mathcal{D}[\frac{1}{N}\sum_{i=1}^Nx_i^2-\mu^2]-\mathbb{E}_\mathcal{D}[\mu_{MLE}^2-\mu^2]=\sigma^2-(\mathbb{E}_\mathcal{D}[\mu_{MLE}^2]-\mu^2)\\&=\sigma^2-(\mathbb{E}_{\mathcal{D}}[\mu_{MLE}^2]-\mathbb{E}_{\mathcal{D}}^2[\mu_{MLE}])=\sigma^2-Var[\mu_{MLE}]\\&=\sigma^2-Var[\frac{1}{N}\sum_{i=1}^Nx_i]=\sigma^2-\frac{1}{N^2}\sum_{i=1}^NVar[x_i]=\frac{N-1}{N}\sigma^2\end{aligned}$

$\hat{\sigma}^2=\frac{1}{N-1}\sum_{i=1}^N(x_i-\mu)^2$

第一步展开平方：

$\mathbb{E}[\sigma_{MLE}^2]=\mathbb{E}\left[\frac{1}{N}\sum_{i=1}^N(x_i-\mu_{MLE})^2\right]\\=\mathbb{E}\left[\frac{1}{N}\sum_{i=1}^N(x_i^2-2x_i\mu_{MLE}+\mu_{MLE}^2)\right]$

第二步拆分期望，并加减 $\mu^{2}$ ：

$=\mathbb{E}\left[\frac{1}{N}\sum_{i=1}^Nx_i^2-\mu_{MLE}^2\right]=\mathbb{E}\left[\frac{1}{N}\sum_{i=1}^Nx_i^2-\mu^2+\mu^2-\mu_{MLE}^2\right]$

第一步：因为 $\frac{1}{N}\sum_{i=1}^N(-2x_i\mu_{MLE}+\mu_{MLE}^2)=-\mu_{MLE}^2$ 。可以验证：
$\begin{aligned}&\frac{1}{N}\sum_{i=1}^N(-2x_i\mu_{MLE})=-2\mu_{MLE}(\frac{1}{N}\sum_{i=1}^Nx_i)=-2\mu_{MLE}^2\\&\frac{1}{N}\sum_{i=1}^N(\mu_{MLE}^2)=\mu_{MLE}^2\end{aligned}$
所以合并后为 $-\mu_{MLE}^2$ 。
第二步：巧妙地加上再减去 $\mu^2$ ，为后续分解做准备。 $\mu$ 是真实的总体均值。

第三步利用期望的线性性质拆分:

$=\mathbb{E}\left[\frac{1}{N}\sum_{i=1}^Nx_i^2-\mu^2\right]-\mathbb{E}\left[\mu_{MLE}^2-\mu^2\right]=\sigma^2-(\mathbb{E}[\mu_{MLE}^2]-\mu^2)$

$\mathbb{E}[\frac{1}{N}\sum_{i=1}^Nx_i^2-\mu^2]=\frac{1}{N}\sum_{i=1}^N\mathbb{E}[x_i^2]-\mu^2$ 。
根据方差的定义 $Var(x_i)=\mathbb{E}[x_i^2]-(\mathbb{E}[x_i])^2$ ，所以 $\mathbb{E}[x_i^2]=Var(x_i)+(\mathbb{E}[x_i])^2=\sigma^2+\mu^2$ 。
代入得： $\frac{1}{N}\sum_{i=1}^N(\sigma^2+\mu^2)-\mu^2=\frac{1}{N}(N\sigma^2+N\mu^2)-\mu^2=\sigma^2+\mu^2-\mu^2=\sigma^2$ 。
所以第一项就是 $\sigma^2$ 。第二项 $\mathbb{E}[\mu_{MLE}^2-\mu^2]=\mathbb{E}[\mu_{MLE}^2]-\mu^2$ 。

第四行再次利用方差定义：

$=\sigma^2-(\mathbb{E}[\mu_{MLE}^2]-\mathbb{E}[\mu_{MLE}]^2)=\sigma^2-Var[\mu_{MLE}]$

注意： $Var(\mu_{MLE})=\mathbb{E}[\mu_{MLE}^2]-(\mathbb{E}[\mu_{MLE}])^2$ 。
而上一步中括号内是 $\mathbb{E}[\mu_{MLE}^2]-\mu^2$ 。因为我们已经证明 $\mathbb{E}[\mu_{MLE}]=\mu$ ，所以 $(\mathbb{E}[\mu_{MLE}])^2=\mu^2$ 。
因此， $\mathbb{E}[\mu_{MLE}^2]-\mu^2=(\mathbb{E}[\mu_{MLE}^2]-(\mathbb{E}[\mu_{MLE}])^2)=Var(\mu_{MLE})$ 。
所以整个表达式简化为 $\sigma^2-Var(\mu_{MLE})$ 。

第五行计算 $\mu_{MLE}$ 的方差：

$=\sigma^2-Var\left[\frac{1}{N}\sum_{i=1}^Nx_i\right]=\sigma^2-\frac{1}{N^2}\sum_{i=1}^NVar[x_i]$

$\mu_{MLE}$ 是样本均值 $\frac{1}{N}\sum x_i$ 。
方差的性质： $Var(aX)=a^2Var(X)$ ，且对于独立随机变量，和方差等于方差之和： $Var(\sum X_i)=\sum Var(X_i)$ 。
因此， $Var(\frac{1}{N}\sum_{i=1}^Nx_i)=\frac{1}{N^2}Var(\sum_{i=1}^Nx_i)=\frac{1}{N^2}\sum_{i=1}^NVar(x_i)$ 。

第六行得出最终结论：

$=\sigma^2-\frac{1}{N^2}\sum_{i=1}^N\sigma^2=\sigma^2-\frac{1}{N^2}(N\sigma^2)=\sigma^2-\frac{\sigma^2}{N}=\frac{N-1}{N}\sigma^2$

因为每个数据点 $x_{i}$ 都来自同一个方差为 $\sigma^2$ 的分布，所以 $Var(x_i)=\sigma^2$ 。
代入后得到 $\frac{1}{N^2}\sum_{i=1}^N\sigma^2=\frac{1}{N^2}(N\sigma^2)=\frac{\sigma^2}{N}$ 。
最终结果： $\mathbb{E}[\sigma_{MLE}^2]=\sigma^2-\frac{\sigma^2}{N}=\frac{N-1}{N}\sigma^2.$ .

第七步构造一个新的估计量 $\hat{\sigma}^2$ ，使得 $\mathbb{E}[\hat{\sigma}^2]=\sigma^2$ （即无偏）：

我们假设这个新估计量与MLE估计量呈简单的比例关系：

$\hat{\sigma}^2=c\cdot\sigma_{MLE}^2=c\cdot\frac{1}{N}\sum_{i=1}^N(x_i-\mu_{MLE})^2$

其中 c是一个待定的修正系数。

我们对这个新的估计量求期望：

$\mathbb{E}[\hat{\sigma}^2]=\mathbb{E}[c\cdot\sigma_{MLE}^2]=c\cdot\mathbb{E}[\sigma_{MLE}^2]=c\cdot\frac{N-1}{N}\sigma^2$

我们希望这个期望等于真正的方差 $\sigma^2$ ：

$c\cdot\frac{N-1}{N}\sigma^2=\sigma^2$

两边同时除以 $\sigma^2$ （假设 $\sigma^2\neq0$ ），解得修正系数 c：

$c\cdot\frac{N-1}{N}=1\\c=\frac{N}{N-1}$

得到：

$\hat{\sigma}^2=\frac{N}{N-1}\cdot\sigma_{MLE}^2\\=\frac{N}{N-1}\cdot\frac{1}{N}\sum_{i=1}^N(x_i-\mu_{MLE})^2\\=\frac{1}{N-1}\sum_{i=1}^N(x_i-\mu_{MLE})^2$

多元高斯分布

一般地，高斯分布的概率密度函数PDF写为：

$p(x|\mu,\Sigma)=\frac{1}{(2\pi)^{p/2}|\Sigma|^{1/2}}\exp\left(-\frac{1}{2}(x-\mu)^T\Sigma^{-1}(x-\mu)\right)$

x: 是一个 $p$ 维的随机变量向量。例如， $x=[x_1,x_2,...,x_p]^T$ ,它可以代表一个人的[身高，体重，年龄],或者一张图片的像素值集合。

p: 数据的维度。

$\mu$ : 是一个p维的均值向量 (Mean Vector) 。 $\mu=[\mu_1,\mu_2,...,\mu_p]^T$ 。它表示这个分布的中
心点，即各维度平均值的集合。它决定了分布的中心位置。

$\Sigma$ :是一个 $p\times p$ 的协方差矩阵 (Covariance Matrix)。这是公式中最关键的部分，它决定了分布的形状(包括 spread(分散程度)和orientation(方向))。

它的对角线元素 $\Sigma_{ii}$ 是第 $i$ 个维度的方差（Variance），控制每个维度上的分散程度。方差越大，数据点在那个维度上就越分散。
它的非对角线元素 $\Sigma_{ij}$ 是第 $i$ 维和第 $j$ 维之间的协方差 (Covariance),控制不同维度之间的线性相关性。协方差为正，表示一个变量增大时另一个也倾向于增大；为负则表示一个增大时另一个减小；为零则表示线性不相关。

$|\Sigma|:$ 是协方差矩阵 $\Sigma$ 的行列式 (Determinant)。它可以粗略地衡量矩阵所代表的线性变换对空间的“拉伸”或”压缩“程度。在这里，它帮助计算分布的”体积”。

$(x-\mu)^T\Sigma^{-1}(x-\mu)$ :这个二次型被称为马哈拉诺比斯距离(Mahalanobis Distance)。它是一个计算点 $x$ 到中心 $\mu$ 的距离的度量，不同于欧氏距离，它考虑了数据的相关性和 scale (尺度)。如果 $\Sigma$ 是单位矩阵，这个距离就退化成了标准的欧氏距离。

直观理解：公式的两大部分

1. 归一化常数部分： $\frac{1}{(2\pi)^{p/2}|\Sigma|^{1/2}}$

作用：确保这个概率密度函数在整个空间上的积分等于1。这是一个概率分布的基本要求。
$(2\pi)^{p/2}$ ：来自一维高斯分布中归一化常数的推广。
$|\Sigma|^{1/2}$ ：协方差矩阵的行列式的平方根。行列式越大(表示数据整体越分散),这个常数就越小，从而将整体的概率密度按比例"压扁”,以保证总积分为1。

2. 指数核心部分： $\exp\left(-\frac{1}{2}(x-\mu)^T\Sigma^{-1}(x-\mu)\right)$

作用：这是真正决定概率相对大小的部分。
指数函数 exp⁡(⋅)保证了结果永远为正。
核心是 $-\frac12(x-\mu)^T\Sigma^{-1}(x-\mu)$ 。当点 $x$ 越靠近中心 $\mu$ 时，马哈拉诺比斯距离越小，指数项的值越大 (因为负得少),因此概率密度越高。当点 $x$ 远离中心 $\mu$ 时，距离变大，指数项的值急剧变小，概率密度也急剧下降。