二叉树的经典算法与应用

1.根据二叉树构建字符串

606. 根据二叉树创建字符串 - 力扣（LeetCode）

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:string tree2str(TreeNode* root) {string str;if(root == nullptr){return str;}str += to_string(root->val);//左不为空需要括起来 但是左为空 右不为空 括号需要保留if(root -> left || root ->right){str += '(';str +=tree2str(root->left);str += ')';}//右不为空都要括起来if(root -> right){str +='(';str += tree2str(root -> right);str +=')';}return str;}
};

2.二叉树的层序遍历I

102. 二叉树的层序遍历 - 力扣（LeetCode）

核⼼思想：我们在层序遍历过程中，增加⼀个levelSize，记录每层的数据个数，树不为空的情况下，第1层levelSize=1，循环控制，第1层出完了，第2层就都进队列了，队列中size就是第2层的数据个数。以此内推，假设levelSize为第n层的数据个数，因为层序遍历思想为当前层结点出队列，带⼊下⼀层结点(也就是⼦结点)，循环控制第n层数据出完了，那么第n+1结点都进队列了，队列size，就是下⼀层的levelSize。

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:vector<vector<int>> levelOrder(TreeNode* root) {vector<vector<int>> vv;int levelsize=0;//当前层数个数，控制数据一层一层出queue<TreeNode*> q;if(root){q.push(root);levelsize=1;}while(!q.empty()){vector<int> v;while(levelsize--){TreeNode* front= q.front();v.push_back(front->val);q.pop();if(front->left){q.push(front->left);}if(front->right){q.push(front->right);}}//当前层出完，下一层都进队列了，队列的size就是下一层的数据levelsize=q.size();vv.push_back(v);}return vv;}
};

3.二叉树的层序遍历II

107. 二叉树的层序遍历 II - 力扣（LeetCode）

只需要把前面的逆置就行。

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:vector<vector<int>> levelOrderBottom(TreeNode* root) {vector<vector<int>> vv;int levelsize=0;//当前层数个数，控制数据一层一层出queue<TreeNode*> q;if(root){q.push(root);levelsize=1;}while(levelsize > 0){vector<int> v;while(levelsize--){TreeNode* front= q.front();v.push_back(front->val);q.pop();if(front->left){q.push(front->left);}if(front->right){q.push(front->right);}}//当前层出完，下一层都进队列了，队列的size就是下一层的数据levelsize=q.size();vv.push_back(v);}reverse(vv.begin(),vv.end());return vv;}
};

4.二叉树的最近公共祖先

236. 二叉树的最近公共祖先 - 力扣（LeetCode）

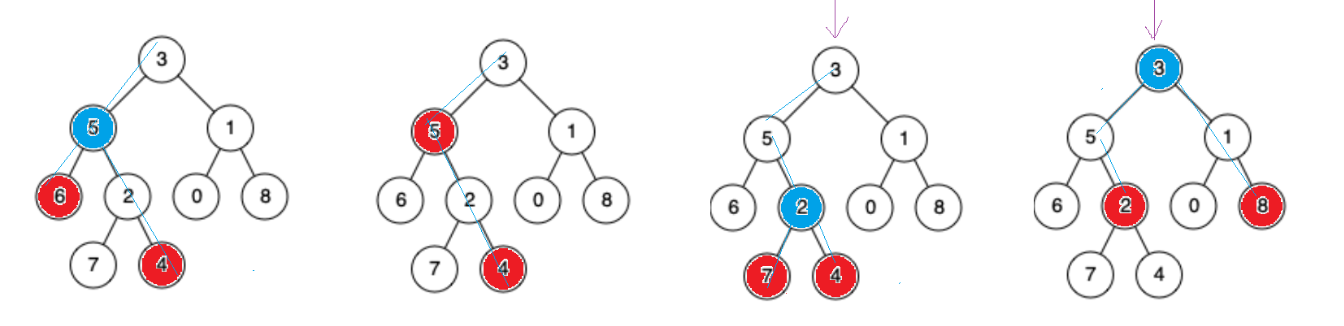
通过观察我们可以发现:

思路1：

仔细观察⼀下，两个结点，最近公共祖先的特征就是⼀个结点在最近公共祖先的左边，⼀个结点在最近公共祖先的右边。⽐如6和4的公共祖先有5和3，但是只有最近公共祖先5满⾜6在左边，4在右边。但是得特殊处理第二个二叉树的情况，我们可以发现这个时候p 和 q 有一个是根节点。

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode(int x) : val(x), left(NULL), right(NULL) {}* };*/
class Solution {
public://在一个子树中查找一个节点是否存在bool IsInTree(TreeNode* t,TreeNode* x){if(t == nullptr){return false;}return t == x || IsInTree(t->left,x) || IsInTree(t->right,x);}TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {if(root == nullptr){return nullptr;}//特殊处理if(p == root || q == root){return root;}bool pInleft = IsInTree(root->left,p);bool pInright = !pInleft;bool qInleft = IsInTree(root->left,q);bool qInright = !qInleft;////1、p和q分别在左和右，root就是最近公共祖先//2、p和q都在左，递归到左子树查找//3、p和q都在右，递归到右子树查找if((pInleft && qInright) || (pInright && qInleft)){return root;}else if(pInleft && qInleft){return lowestCommonAncestor(root->left,p,q);}else{return lowestCommonAncestor(root->right,p,q);}}
};

思路2：

如果能求出两个结点到根的路径，那么就可以转换为链表相交问题。如：6到根3的路径为6-

>5->3，4到根3的路径为4->2->5->3，那么看做两个链表找交点，交点5就是最近公共祖先。

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode(int x) : val(x), left(NULL), right(NULL) {}* };*/
class Solution {
public:bool GetPath(TreeNode* root,TreeNode*x,stack<TreeNode*>& path){//深度遍历前序查找，顺便用栈记录路径if(root == nullptr) return false;path.push(root);// 遇到root结点先push⼊栈，因为root就算不是x，但是root可能是根->x路径中⼀个分⽀结点if(root == x) return true;//root !=x 去左右子树查找if(GetPath(root->left,x,path)){return true;}if(GetPath(root->right,x,path)){return true;}// 如果左右⼦树都没有x，那么说明上⾯⼊栈的root不是根->x路径中⼀个分⽀结点// 所以要pop出栈，回退，继续去其他分⽀路径进⾏查找path.pop();return false;}TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {stack<TreeNode*> pPath;stack<TreeNode*> qPath;GetPath(root,p,pPath);GetPath(root,q,qPath);//找交点while(pPath.size() != qPath.size()){//大的先走if(pPath.size() > qPath.size()){pPath.pop();}else{qPath.pop();}}//一起走while(pPath.top() != qPath.top()){pPath.pop();qPath.pop();}return pPath.top();}
};

5.将二叉搜索树转化为排序的双向链表

LCR 155. 将二叉搜索树转化为排序的双向链表 - 力扣（LeetCode）

思路1：

中序遍历搜索⼆叉树，遍历顺序是有序的，将⼆叉树的结点指针放到⼀个vector中，再把前后

结点的链接关系进⾏修改。这个思路最简单，但是需要消耗O(N)的空间复杂度。

/*
// Definition for a Node.
class Node {
public:int val;Node* left;Node* right;Node() {}Node(int _val) {val = _val;left = NULL;right = NULL;}Node(int _val, Node* _left, Node* _right) {val = _val;left = _left;right = _right;}
};
*/
class Solution {
public:void _treeToDoublyList(Node* root,vector<Node*>& v){if(root == nullptr) return;_treeToDoublyList(root->left,v);v.push_back(root);_treeToDoublyList(root->right,v);}Node* treeToDoublyList(Node* root) {if(root == nullptr) return root;vector<Node*> v;_treeToDoublyList(root,v);for(int i = 0; i<v.size() -1;i++){v[i]->right = v[i+1];v[i+1]->left = v[i];}v[0]->left =v[v.size() - 1];v[v.size() - 1]->right = v[0];return v[0];}
};

思路2：

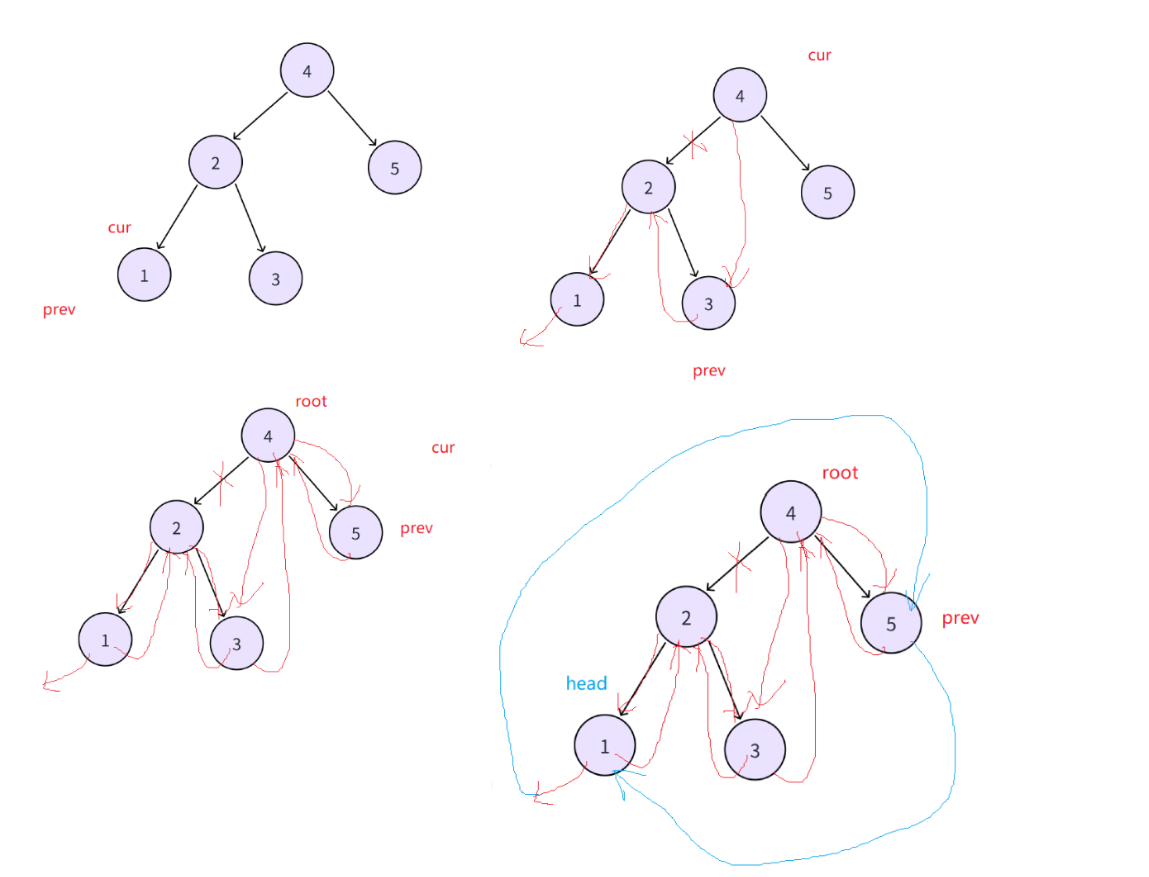
依旧中序遍历搜索⼆叉树，遍历顺序是有序的，遍历过程中修改左指针为前驱和右指针为后继

指针。记录⼀个cur和prev，cur为当前中序遍历到的结点，prev为上⼀个中序遍历的结点，cur->left指向prev，cur->right⽆法指向中序下⼀个，因为不知道中序下⼀个是谁，但是prev->right指向cur； 也就是说每个结点的左是在中遍历到当前结点时修改指向前驱的，但是当前结点的右，是在遍历到下⼀个结点时，修改指向后继的。

/*
// Definition for a Node.
class Node {
public:int val;Node* left;Node* right;Node() {}Node(int _val) {val = _val;left = NULL;right = NULL;}Node(int _val, Node* _left, Node* _right) {val = _val;left = _left;right = _right;}
};
*/
class Solution {
public:void Inorder(Node* cur,Node*& prev){//中序遍历if(cur == nullptr)return;Inorder(cur->left,prev);//left指向中序前一个，左变成前驱cur->left = prev;//中序前一个节点的右指向cur，右变成后继if(prev)prev->right = cur;prev =cur;Inorder(cur->right,prev);}Node* treeToDoublyList(Node* root) {if(root == nullptr) return nullptr;Node* prev =nullptr;Inorder(root,prev);//找头Node* head = root;while(head->left){head = head->left;}//循环链表head->left = prev;prev->right = head;return head;}
};

6. 从前序和中序遍历序列构造二叉树

105. 从前序与中序遍历序列构造二叉树 - 力扣（LeetCode）

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:TreeNode* build(vector<int>& preorder, vector<int>& inorder,int& previ,int begini,int endi){if(begini > endi)return nullptr;//前序确定根TreeNode* root = new TreeNode(preorder[previ]);int rooti = begini;while(begini <= endi){if(inorder[rooti] == preorder[previ]){break;}else{rooti++;}}previ++;//分割区间//[begini,rooti-1] rooti [rooti+1,endi]root->left = build(preorder,inorder,previ,begini,rooti - 1);root->right = build(preorder,inorder,previ,rooti+1,endi);return root;}TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {int i =0;return build(preorder,inorder,i,0,inorder.size() - 1);}
};

7.从中序和后序遍历序列构造二叉树

106. 从中序与后序遍历序列构造二叉树 - 力扣（LeetCode）

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:TreeNode* build(vector<int>& inorder, vector<int>& postorder,int& posti,int begini,int endi){if(begini > endi)return nullptr;TreeNode* root = new TreeNode(postorder[posti]);int rooti = begini;//找到根的位置while(begini <= endi){if(inorder[rooti] == postorder[posti]){break;}else{rooti++;}}posti--;//先构建右子树 再构建左子树root->right = build(inorder,postorder,posti,rooti+1,endi);root->left = build(inorder,postorder,posti,begini,rooti-1);return root;}TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {int posti = postorder.size() - 1;return build(inorder,postorder,posti,0,inorder.size() -1);}
};

8.二叉树的前序遍历非递归

144. 二叉树的前序遍历 - 力扣（LeetCode）

⾮递归迭代实现思想：

要迭代⾮递归实现⼆叉树前序遍历，⾸先还是要借助递归的类似的思想，只是需要把结点存在栈中，⽅便类似递归回退时取⽗路径结点。跟这⾥不同的是，这⾥把⼀棵⼆叉树分为两个部分：

1. 先访问左路结点

2. 再访问左路结点的右⼦树

这⾥访问右⼦树要以循环从栈依次取出这些结点，循环⼦问题的思想访问左路结点的右⼦树。

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:vector<int> preorderTraversal(TreeNode* root){stack<TreeNode*> st;vector<int> v;TreeNode* cur = root;while(cur || !st.empty()){//每次循环开始代表访问一棵树的开始//访问左路节点，左路节点入栈while(cur){st.push(cur);v.push_back(cur->val);cur = cur->left;}//取一个左路节点的右子树来访问TreeNode* top = st.top();st.pop();//循环子问题访问右子树cur = top->right;}return v;}
};

9.二叉树的中序遍历非递归

中序和后序跟前序的思路完全⼀致，只是前序先访问根还是后访问根的问题。

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:vector<int> inorderTraversal(TreeNode* root) {stack<TreeNode*> st;vector<int> v;TreeNode* cur = root;while(cur || !st.empty()){//每次循环开始代表访问一棵树的开始//访问左路节点，左路节点入栈while(cur){st.push(cur);cur = cur->left;}//取一个左路节点的右子树来访问TreeNode* top = st.top();st.pop();v.push_back(top->val);//循环子问题访问右子树cur = top->right;}return v;   }
};

10.二叉树的后序遍历非递归

后序稍微⿇烦⼀些，因为后序遍历的顺序是左⼦树 右⼦树 根，当取到左路结点的右⼦树时，需要想办法标记判断右⼦树是否访问过了（可能会死循环），如果访问过了，就直接访问根，如果没有访问过需要先访问右⼦树。

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:vector<int> postorderTraversal(TreeNode* root) {stack<TreeNode*> st;vector<int> v;TreeNode* cur = root;//记录上一个后序访问的节点TreeNode* prev = nullptr;while(cur || !st.empty()){//每次循环开始代表访问一棵树的开始//访问左路节点，左路节点入栈while(cur){st.push(cur);cur = cur->left;}//取一个左路节点的右子树来访问，这时代表左路节点的左子树已经访问过了TreeNode* top = st.top();//如果右为空或者上一个访问的节点是右子树的根，代表右子树也访问过了//可以访问当前节点if(top->right == nullptr || prev == top->right){v.push_back(top->val);st.pop();//只要一个已经访问过了把它给上一个访问的节点prev = top;}//右不为空else{//循环子问题访问右子树cur = top->right;}}return v;   }
};