控制建模matlab练习16:线性状态反馈控制器-⑤轨迹追踪
此练习,主要是使用状态空间方程来设计控制器的方法和思路:
①系统建模;
②系统的能控性;
③极点配置;
④最优化控制LQR;
⑤轨迹追踪;
以下是,第⑤部分:轨迹追踪;
一、问题引出
- 从前面几节练习的控制器设计,都是围绕最后的平衡点在角度和角速度都为0,即 zf=[0,0]T 进行分析;
- 如果,设计的目标是将系统的状态稳定在一个非零的目标值 zd=[z1d,z2d]T ,该如何设计呢?
二、轨迹追踪设计
- 设计 u(t)使得系统状态稳定在一个非0的目标值 zd ;
- 此时,需要控制量 u(t)(即动态系统的输入)有两个功能;
- ①改变系统的平衡点位置到 zd ;
- ②令 zd 成为一个稳定的平衡点。
- 书中通过推导分析,角速度 z2d 的唯一平衡点只能是0;
- 而角度 z1d 的平衡点是可以通过输入 u(t)改变的;
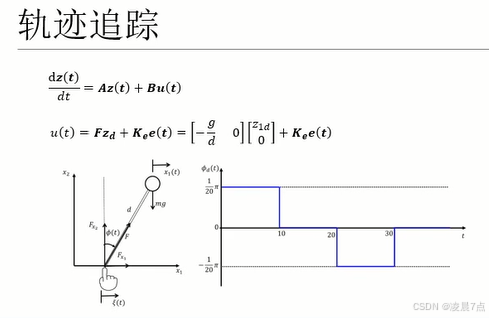
- 从下图,
- 0<t<10时,是 π/20 ;
- 在10<t<20时,是 0 ;
- 在20<t<30时,是 -π/20 ;
- 令:
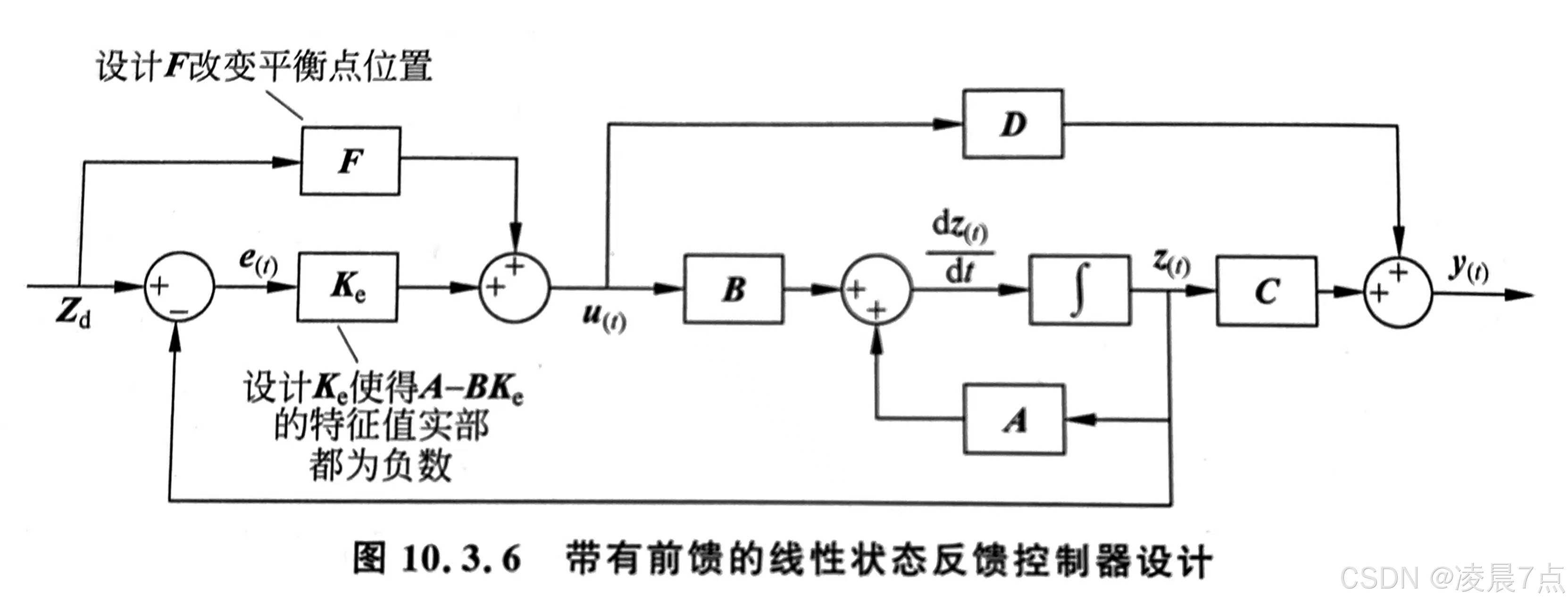
u(t)=Fzd+Kee(t) u(t)=Fz_d+K_ee(t) u(t)=Fzd+Kee(t) - Fzd 是:前馈,用来将平衡点从 z1f 移动到 z1d ;
- Kee(t) 是:用来配置极点,使得系统稳定;
- e(t) 是:系统误差,将以误差来进行分析,误差状态平衡点为 ef=[0,0]T
- 在MATLAB中的代码如下,包括两个文件①Tracking.m、②sys.m。
- 其中,ode45是一种解线性微分方程的算法:
- @sys:输入,系统
- tspan:输入,时间区间
- z0:输入,状态变量初始值,z0 = [0;0];从0开始的
- t,输出,时间
- z,输出,状态变量
%% Tracking.m %%
clc;clear;close all;
%% 定义仿真区间
tspan =[0 40];
z0 = [0;0];
%% 求解
[t,z]=ode45(@sys,tspan,z0);
hold on;
plot (t,z(:,1));
grid on;
%% sys.m %%
%% 使用时需与Tracking.m在同一文件夹内
function dz = sys(t, z)
%% 定义参数g=10;d=1;
%% 定义矩阵A=[0 1;g/d 0];B=[0;1];C = [1, 0];D = 0;
%% 定义目标zdif t >= 0 & t <10z1d = pi/20;elseif t >= 20 & t <30z1d = -pi/20;elsez1d = 0;end %% 定义状态空间方程zd = [z1d; 0];%%平衡点位置Ke = [25, 7];%%书中已经求出的结果F = [-g/d, 0]; %%前馈e = zd - z; %%误差u = F * zd + Ke*e;dz = A*z + B*u;
end
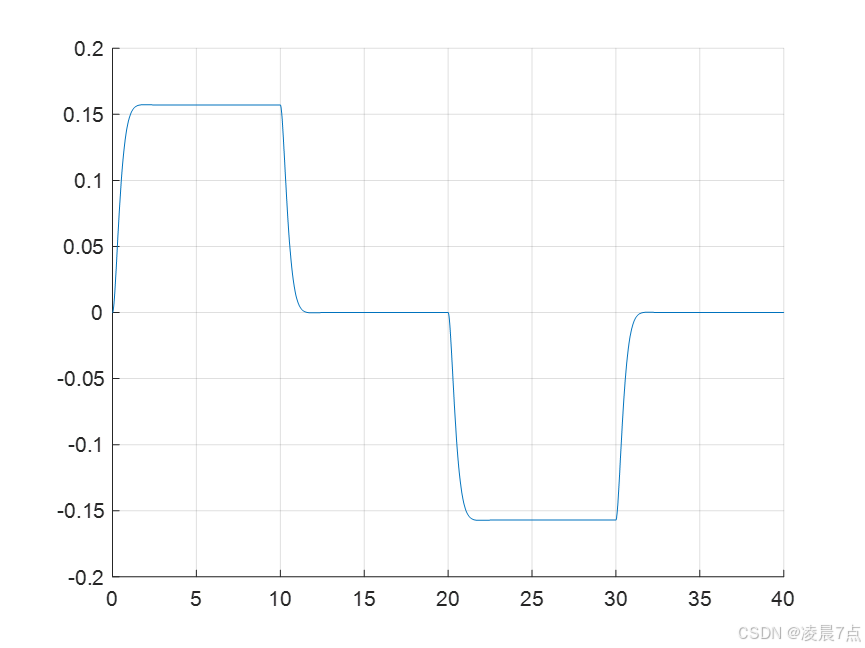
三、运行结果
- 从图看出,可以很好的追踪到目标位置;
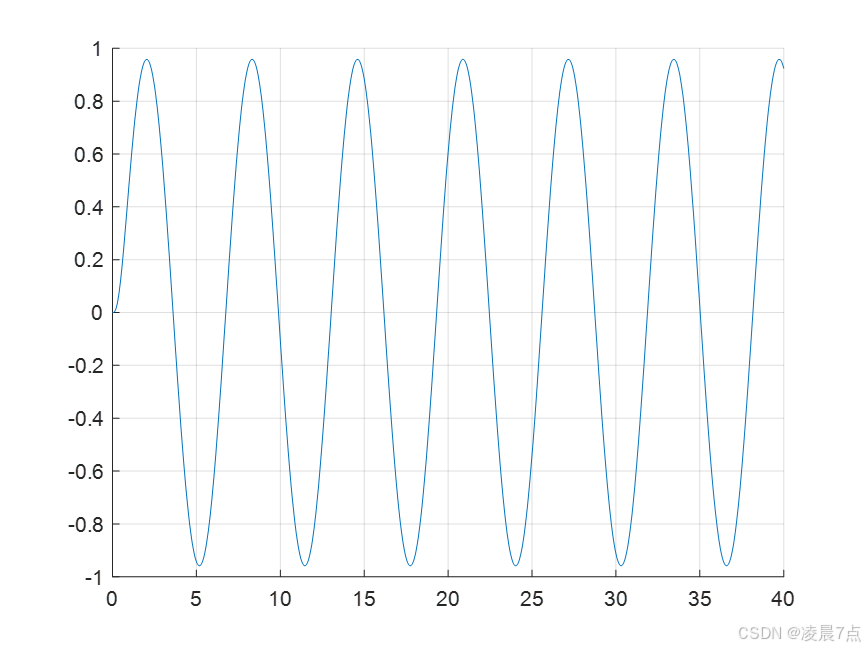
- 同样,ode45也能追踪非线性的,例如将sys.m文件中的这部分修改:
- 将 z1d=sin(t) ,再看看同样能追踪到sin函数;
%% 定义目标zd% if t >= 0 & t <10% z1d = pi/20;% elseif t >= 20 & t <30% z1d = -pi/20;% else% z1d = 0;% end z1d = sin(t);
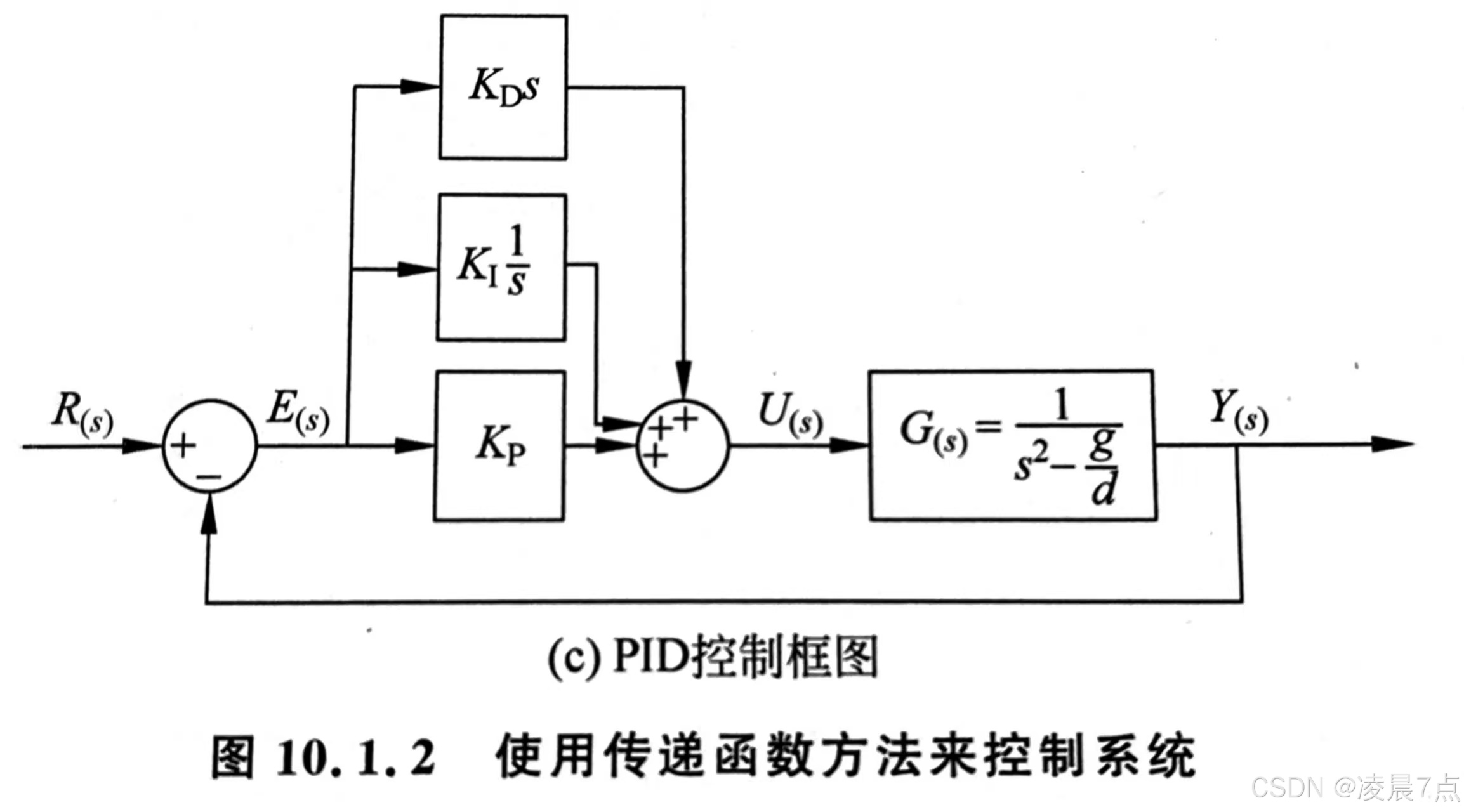
四、与PID的比较
- 使用PID的控制框图:
- 使用本练习的,带有前馈的线性状态反馈控制器设计:
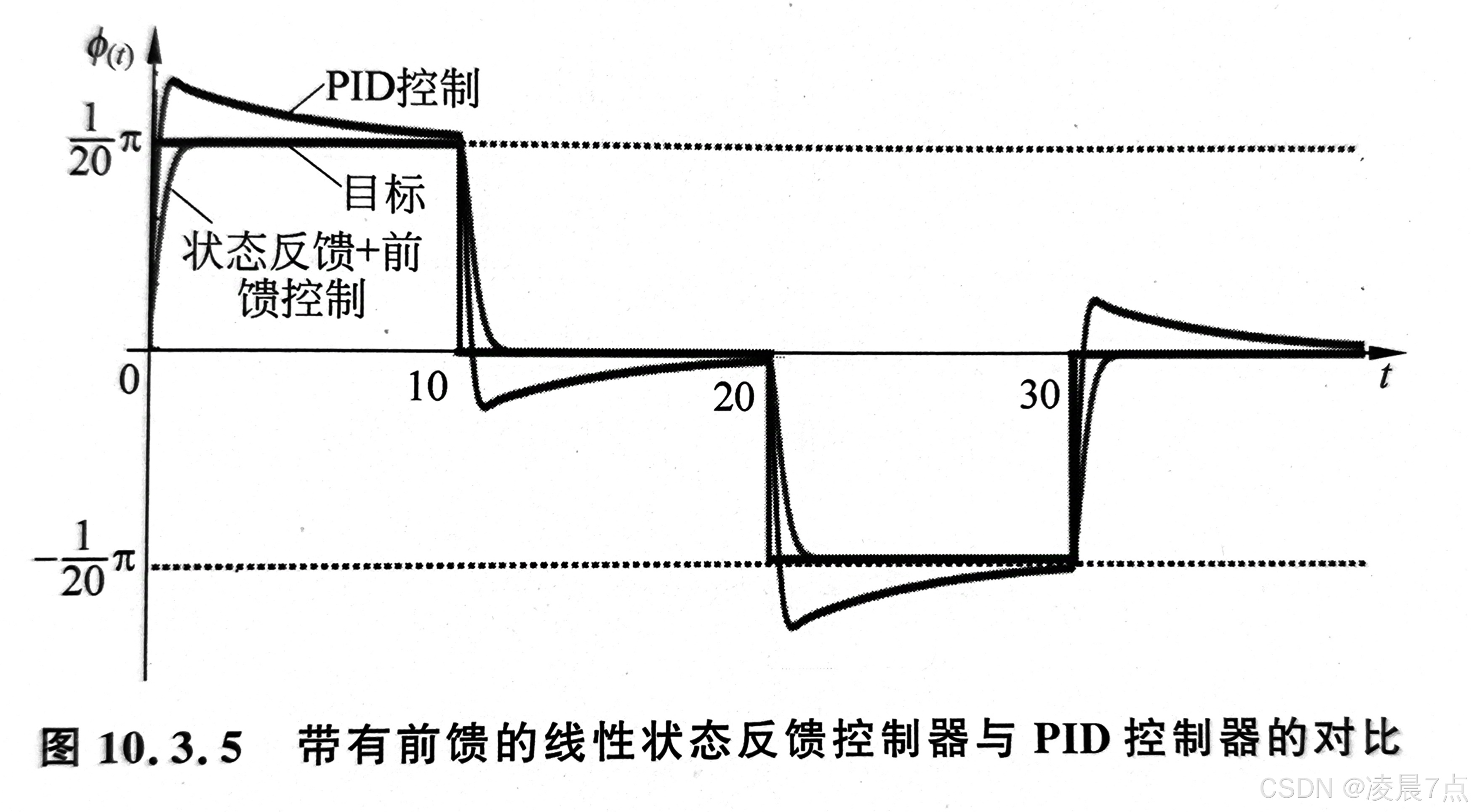
- 书中的对比结果:(如下图)
- 因为PID控制只使用输出的误差信号 e(t) 来设计控制器;
- 线性状态反馈控制器的设计,则用到所有状态变量 z(t) 来设计。
- 因为有更多的系统信息被用来设计控制器,所以状态反馈控制器的灵活度更大,有更多可调节的参数,也就更有可能达到满意的表现。
学习来源:《控制之美》[卷1],王天威
