当前位置：首页 > news >正文

[e3nn] docs | 不可约表示(Irreps)

news 2025/8/23 20:03:17

链接：https://docs.e3nn.org/en/latest/examples/examples.html

在这里插入图片描述

docs：e3nn

e3nn是一个用于构建欧几里得(E(3))等变神经网络的Python库，这意味着它们能自动保持三维旋转和反射的对称性。

该库使用不可约表示(Irreps)来描述数据变换方式，通过张量积以原则性的方式组合这些对称特征。

此外，该库还利用球谐函数处理方向性数据，提供专门的等变神经网络模块（如线性层和激活函数），包含用于稳定训练的归一化策略，并支持TorchScript JIT以实现优化部署。

可视化

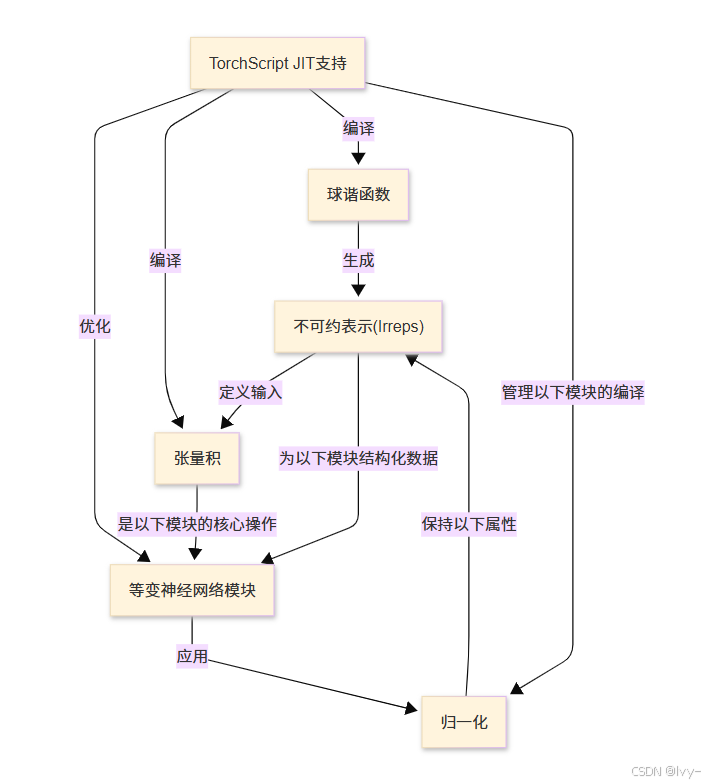
在这里插入图片描述

章节列表

不可约表示(Irreps)
球谐函数
张量积
等变神经网络模块
归一化
TorchScript JIT支持

e3nn库文档

该库旨在帮助开发E(3)等变神经网络，包含张量积和球谐函数等基础数学运算。

请添加图片描述

快速入门

import torch
from e3nn import o3# 创建由标量(0e)和向量(1o)组成的随机数组
irreps_in = o3.Irreps("0e + 1o")
x = irreps_in.randn(-1)# 应用线性层
irreps_out = o3.Irreps("2x0e + 2x1o")
linear = o3.Linear(irreps_in=irreps_in, irreps_out=irreps_out)
y = linear(x)# 计算自张量积
tp = o3.FullTensorProduct(irreps_in1=irreps_in, irreps_in2=irreps_in)
z = tp(x, x)# 可选：编译张量积运算
tp_pt2 = torch.compile(tp, fullgraph=True)
z_pt2 = tp_pt2(x, x)  # 注意：由于编译过程，前几次调用可能较慢
torch.testing.assert_close(z, z_pt2)

安装指南

重要提示：请先安装PyTorch，再执行以下命令

pip install --upgrade pip
pip install --upgrade e3nn

详细安装说明和可选依赖项请参阅INSTALL.md文件

版本变更说明

e3nn目前处于开发阶段。建议使用pip安装。主分支被视为不稳定版本。当代码发生破坏性变更时，次版本号会递增。

版本号格式：
0.(破坏性变更时递增).(兼容性更新时递增)

第1章：不可约表示(Irreps)

欢迎来到e3nn的精彩世界🐻‍❄️

这个库能帮助我们构建对三维空间中物体行为"有认知"的神经网络，特别是在物体旋转或反射时。

想象训练一个神经网络来理解分子。
当你旋转一个分子时，它仍然是同一个分子！
真正智能的网络应该能识别这一点，而无需展示所有可能的旋转。

这种特性被称为**等变性**，而e3nn使之成为可能。

e3nn的核心是一个称为不可约表示(简称Irreps)的基本概念。

可以将Irreps视为标签，告诉e3nn你的数据代表哪种物理量。
这个标签至关重要，因为它决定了当三维世界旋转或反射时，数据应如何表现。

让我们从一个简单例子开始。假设你有一个球的两条信息：

温度：这是一个单一数字。旋转球时，其温度(比如在中心点)不会改变。
位置处的风向和风速：这是一个矢量，既有大小又有方向。旋转球时，风矢量会随之改变旋转。

温度(标量)和风(矢量)在旋转下的表现不同。e3nn需要知道这种差异来构建等变神经网络。这正是Irreps提供的功能

什么是`Irrep`(单数)？

一个Irrep(发音为"ear-rep")描述一种基本的信息"类型"或"类别"，是最小的构建模块。

每个Irrep由两个关键属性定义：

l(角动量/阶数)：这是一个非负整数(0,1,2,…)
- l=0：表示标量。如温度示例，标量是旋转坐标系时不变的单一数字。
- l=1：表示矢量。如风示例，矢量有方向和大小，会随物体旋转。
- l=2及以上：表示更复杂的量，有时称为张量或多极子，在旋转下以特定方式变换。
阶数为l的Irrep维度总是2l + 1。因此标量(l=0)维度为1，矢量(l=1)维度为3。
p(宇称)：取值为+1(偶，记作’e’)或-1(奇，记作’o’)。宇称描述数据在反射(如镜面反射)时的行为：
- 偶宇称(e)：反射后数据保持不变。标量温度(0e)具有偶宇称。
- 奇宇称(o)：反射后数据符号或方向翻转。矢量(1o)具有奇宇称——如果反射一个指向右侧的矢量，它将指向左侧(其分量符号翻转)。

e3nn使用简洁的字符串表示法。例如：

0e：偶宇称标量(l=0)
1o：奇宇称矢量(l=1)，这是表示3D矢量的标准方式
2e：偶宇称张量(l=2)

可以在e3nn中这样创建Irrep对象：

from e3nn.o3 import Irrep# 标量(l=0, 偶宇称)
scalar_irrep = Irrep("0e")
print(f"标量Irrep: {scalar_irrep}, l={scalar_irrep.l}, p={scalar_irrep.p}, 维度={scalar_irrep.dim}")# 矢量(l=1, 奇宇称)
vector_irrep = Irrep("1o")
print(f"矢量Irrep: {vector_irrep}, l={vector_irrep.l}, p={vector_irrep.p}, 维度={vector_irrep.dim}")

输出：

标量Irrep: 0e, l=0, p=1, 维度=1
矢量Irrep: 1o, l=1, p=-1, 维度=3

什么是`Irreps`(复数)？

现实世界的数据通常不是单一标量或矢量，而是不同类型信息的组合。

例如空间中的一个点可能同时具有温度(标量)和速度(矢量)。

这时就需要Irreps(复数)。Irreps对象描述多个Irrep类型的集合或直和，就像是复杂数据结构的配方。

Irreps的字符串表示法组合了单个Irrep字符串，通常带有"多重性"数字表示特定Irrep类型出现的次数：

1x0e：一个标量(单实例时1x可省略)
2x0e：两个独立标量
0e + 1o：一个标量和一个矢量
3x0e + 5x1o + 2x2e：三个标量、五个矢量和两个l=2偶宇称张量

创建Irreps对象的方式：

from e3nn.o3 import Irreps# 一个标量和一个矢量的组合
my_irreps = Irreps("0e + 1o")
print(f"我的Irreps: {my_irreps}")
print(f"总维度: {my_irreps.dim}")# 更复杂的组合
complex_irreps = Irreps("2x0e + 1x1o + 1x2e")
print(f"复杂Irreps: {complex_irreps}")
print(f"总维度: {complex_irreps.dim}")

输出：

我的Irreps: 1x0e+1x1o
总维度: 4
复杂Irreps: 2x0e+1x1o+1x2e
总维度: 9

注意complex_irreps的总维度计算为：
(2 * (2*0 + 1))(两个0e标量) +
(1 * (2*1 + 1))(一个1o矢量) +
(1 * (2*2 + 1))(一个2e张量) =
(2 * 1) + (1 * 3) + (1 * 5) = 2 + 3 + 5 = 10。

`e3nn`如何使用`Irreps`

Irreps对象本质上是数据在e3nn神经网络中流动的蓝图。

当在e3nn中定义层时，需要指定其输入和输出的Irreps。

以下是e3nnREADME中的示例：

import torch
from e3nn import o3# 定义输入数据的Irreps：一个标量和一个矢量的组合
irreps_in = o3.Irreps("0e + 1o")
print(f"输入Irreps: {irreps_in}")# 创建符合这些Irreps的随机输入数据
x = irreps_in.randn(10, -1) # 10个样本，-1会被替换为irreps_in.dim(4)
print(f"输入数据形状: {x.shape}")# 定义输出数据的Irreps：两个标量和两个矢量的组合
irreps_out = o3.Irreps("2x0e + 2x1o")
print(f"输出Irreps: {irreps_out}")# 创建将'irreps_in'数据转换为'irreps_out'数据的线性层
# e3nn确保该层保持旋转/反射等变性
linear = o3.Linear(irreps_in=irreps_in, irreps_out=irreps_out)
print(f"创建的线性层: {linear}")# 将线性层应用于输入数据
y = linear(x)
print(f"输出数据形状: {y.shape}")

输出：

输入Irreps: 1x0e+1x1o
输入数据形状: torch.Size([10, 4])
输出Irreps: 2x0e+2x1o
创建的线性层: Linear(1x0e+1x1o -> 2x0e+2x1o)
输出数据形状: torch.Size([10, 8])

注意o3.Linear以irreps_in和irreps_out为参数。

这告诉层如何解释其输入以及应产生何种输出，同时保持等变性。

内部机制：Irreps的结构

快速了解e3nn如何存储这些Irrep和Irreps对象：

classDiagramdirection LRclass Irrep {+int l+int p+dim: int}class _MulIr {+int mul+Irrep ir+dim: int}class Irreps {+tuple[tuple] internal_structure+dim: int+num_irreps: int}Irreps "1" * "0..*" _MulIr_MulIr "1" * "1" Irrepnote for Irrep: 表示单个不可约表示(如1o)note for _MulIr: 将多重性与Irrep结合(如2x0e)note for Irreps: _MulIr对象的集合(直和)(如2x0e+1x1o)

Irrep：存储为包含(l, p)的简单tuple。例如Irrep("1o")内部是(1, -1)，其dim属性计算为2l+1。
_MulIr：另一个简单tuple，包含(多重性, Irrep_object)。所以2x0e会是(2, Irrep(0, 1))，其dim计算为多重性 * Irrep_object.dim。
Irreps：_MulIr对象的tuple。当给出字符串如Irreps("2x0e + 1x1o")时，它会解析字符串，创建_MulIr(2, Irrep(0, 1))和_MulIr(1, Irrep(1, -1))，并将它们存储在元组中。其dim属性是所有_MulIr组件维度的总和。

当要求Irreps对象提供其变换矩阵(如通过irreps.D_from_matrix(R))时，e3nn会为每个单独的Irrep计算变换矩阵(使用称为wigner_D的函数，我们将在下一章详细介绍)，然后将它们组合成一个大的块对角矩阵。这种块对角结构意味着每种Irrep类型独立变换，这是不可约表示的关键特性。

`Irrep`与`Irreps`快速对比

特性	`Irrep`(单数)	`Irreps`(复数)
概念	单一基本的数据变换类型	多个`Irrep`类型的集合或"直和"
属性	`l`(阶数)和`p`(宇称)	`(多重性, Irrep)`对的列表
示例	`0e`(标量), `1o`(矢量)	`2x0e + 1o`(两个标量和一个矢量)
维度	`2l + 1`	所有组件的`多重性 * (2l + 1)`之和
用途	定义单个组件	定义`e3nn`中数据的整体结构