数学建模-灰色关联分析
目录
1-AI带你认识GRA
📘 一、灰色关联分析(GRA)简介
1. 什么是灰色关联分析?
2. 核心思想(通俗理解):
3. 与熵权法的对比(快速类比):
🧩 二、灰色关联分析的基本原理
1. 问题背景:
🛠️ 三、灰色关联分析的基本步骤(标准流程)
✅ 步骤 1:构建原始数据矩阵
✅ 步骤 2:确定参考序列(理想解/母序列)
✅ 步骤 3:数据标准化(无量纲化处理)
(1)均值化法(常用):
(2)初值化法:
(3)区间化法(极差标准化):
✅ 步骤 4:计算关联系数
✅ 步骤 5:计算关联度
✅ 步骤 6:排序与分析
✅ 四、灰色关联分析的优点与缺点
✅ 优点:
❌ 缺点:
📚 五、灰色关联分析的典型应用场景
🧠 六、总结一句话:
📘 类比记忆(帮你更好理解):
📝 在数学建模/论文中的表述建议:
2-理论知识
介绍
定义
应用
3-基于excel表格实现灰色关联分析
1-AI带你认识GRA
📘 一、灰色关联分析(GRA)简介
1. 什么是灰色关联分析?
灰色关联分析(Grey Relational Analysis,简称 GRA 或 灰色关联度分析) 是一种分析系统中各因素间关联程度(相似程度、变化趋势相似性)的定量方法,由我国著名学者 邓聚龙教授 在 20 世纪 80 年代提出,是灰色系统理论的重要组成部分。
2. 核心思想(通俗理解):
灰色关联分析的核心思想是:通过计算各评价对象(或因素)的指标数据序列与“参考序列”(理想或对比基准)之间的“关联程度”(即相似程度、变化趋势的相近程度),来判断它们之间的关联性强弱,从而进行排序、评价或因素分析。
你可以把它理解为:
“谁的变化趋势跟参考对象最像,谁就跟参考对象的关系最紧密,关联度就越高。”
3. 与熵权法的对比(快速类比):
项目
熵权法
灰色关联分析(GRA)
目的
确定各指标的客观权重
分析各对象或因素与参考序列的关联程度(相似性)
输入
原始数据矩阵(指标值)
原始数据矩阵(指标值),通常也需要参考序列
输出
各指标的权重值
各对象与参考对象的关联度,用于排序或分析
是否排序
一般不直接排序,常与 TOPSIS 等方法结合使用
可直接排序,也可用于因素分析
主要用途
多指标综合评价中确定指标重要性
评价对象优劣排序、因素重要性分析、系统趋势分析
特点
基于信息熵,反映指标的区分度
基于序列间的几何相似性,反映变化趋势的相似程度
🧩 二、灰色关联分析的基本原理
1. 问题背景:
在实际问题中,我们常常需要分析:
- •
多个评价对象(如不同城市、企业、方案)在多个指标上的表现;
- •
或者多个因素(如经济指标、环境变量)之间的相互关系与影响程度;
- •
但我们往往缺乏足够的信息(数据少、信息不完全),属于“贫信息、小样本”问题 → 这正是灰色系统理论擅长处理的领域!
👉 灰色关联分析正是用来解决这类“信息不完全但有一定规律”的问题,通过分析数据序列的相似性(关联度)来进行评价或分析。
🛠️ 三、灰色关联分析的基本步骤(标准流程)
假设我们有:
- •
m 个评价对象(如方案、城市、企业)
- •
n 个评价指标
- •
每个对象在每个指标上都有一个观测值
我们要分析这些对象与某个参考对象(理想方案/参考序列)的关联程度,或者直接对这些对象进行优劣排序。
✅ 步骤 1:构建原始数据矩阵
设有 m 个对象,n 个指标,构建原始数据矩阵:
X=x11x21⋮xm1x12x22⋮xm2⋯⋯⋱⋯x1nx2n⋮xmn其中,xij表示第 i 个对象在第 j 个指标上的值。
✅ 步骤 2:确定参考序列(理想解/母序列)
参考序列可以是:
- •
人为指定的最优值(如各指标的最大值/最小值,视指标性质而定)
- •
实际数据中表现最好的那个对象(即某一行数据)
- •
或者根据问题背景自定义的参考标准
一般记作:
X0=(x0(1),x0(2),...,x0(n))如果是对象间的优劣排序问题,通常将每个指标的最优值组合成参考序列(类似 TOPSIS 的正理想解);也可以直接把某个对象作为参考对象。
✅ 步骤 3:数据标准化(无量纲化处理)
由于不同指标的量纲(单位)和数量级不同,通常需要对原始数据进行标准化处理,常用方法有:
(1)均值化法(常用):
xi′(k)=x(k)xi(k),x(k)=m1i=1∑mxi(k)(2)初值化法:
xi′(k)=xi(1)xi(k)(3)区间化法(极差标准化):
xi′(k)=max(x(k))−min(x(k))xi(k)−min(x(k))推荐使用 均值化法 或 初值化法,在灰色关联分析中较为常见。
标准化后得到新的矩阵 X′。
✅ 步骤 4:计算关联系数
对于每个评价对象 i 与参考序列在每个指标 k 上的数值,计算它们之间的关联系数:
ξi(k)=∣x0(k)−xi′(k)∣+ρ⋅imaxkmax∣x0(k)−xi′(k)∣iminkmin∣x0(k)−xi′(k)∣+ρ⋅imaxkmax∣x0(k)−xi′(k)∣其中:
- •
∣x0(k)−xi′(k)∣:参考序列与第 i 个对象在第 k 个指标上的绝对差
- •
iminkmin和 imaxkmax:两级最小差与最大差(用于规范化和调节)
- •
ρ:分辨系数,一般取 0.5(用于削弱最大差过大带来的影响)
关联系数 ξi(k)反映的是第 i 个对象在第 k 个指标上与参考对象的相似程度(关联程度),取值范围为 [0,1],越接近 1 表示关联越强。
✅ 步骤 5:计算关联度
对每个对象 i,在所有指标上的关联系数求平均值(或加权平均),得到该对象与参考序列的关联度:
ri=n1k=1∑nξi(k)如果各指标的重要程度不同,也可以引入权重 wk,采用加权平均:
ri=k=1∑nwk⋅ξi(k),k=1∑nwk=1
✅ 步骤 6:排序与分析
- •
根据关联度 ri从大到小排序
- •
关联度越大,表示该对象与参考对象越相似,综合表现越好(或关系越紧密)
- •
可用于:
- •
多对象优劣排序
- •
因素重要性分析
- •
系统动态变化趋势分析
✅ 四、灰色关联分析的优点与缺点
✅ 优点:
- 1.
对数据要求低:不需要大量数据,适合小样本、贫信息问题(灰色系统特色)
- 2.
计算简单、易于理解和实现
- 3.
不需要指标数据服从特定分布
- 4.
能反映数据间的变化趋势与相似性,而不仅是数值大小
- 5.
广泛应用于因素分析、方案排序、政策评价等实际问题
❌ 缺点:
- 1.
分辨系数 ρ 的选取具有一定主观性
- 2.
对参考序列的选取比较敏感,影响最终结果
- 3.
只反映关联程度,不直接给出“优劣”的绝对评价,更多是“相似性”
- 4.
一般需结合其他方法(如熵权法、TOPSIS)进行综合评价
📚 五、灰色关联分析的典型应用场景
- •
多方案/多对象优劣排序(如企业绩效、城市发展水平、投资方案等)
- •
因素重要性分析(如分析哪些因素对目标影响最大)
- •
系统趋势分析(如分析某指标与参考目标的变化趋势是否相近)
- •
与 TOPSIS、熵权法等结合使用,构建更强大的综合评价模型
🧠 六、总结一句话:
灰色关联分析是一种通过计算数据序列之间几何形状的相似程度(关联度),来判断各评价对象与参考对象之间关联性强弱的方法,适用于小样本、多指标、贫信息的综合评价与因素分析问题。
📘 类比记忆(帮你更好理解):
可以把灰色关联分析类比为:
“在众多曲线(各对象的数据序列)中,找出哪一条跟参考曲线(理想/基准序列)的‘走势’最像,最像的就说明关联度最高,评价越好。”
📝 在数学建模/论文中的表述建议:
“本文采用灰色关联分析方法,通过构建标准化数据序列与参考序列,计算各评价对象与参考对象的灰色关联系数及关联度,根据关联度大小对评价对象进行优劣排序或因素重要性分析,从而为决策提供依据。”
2-理论知识
介绍

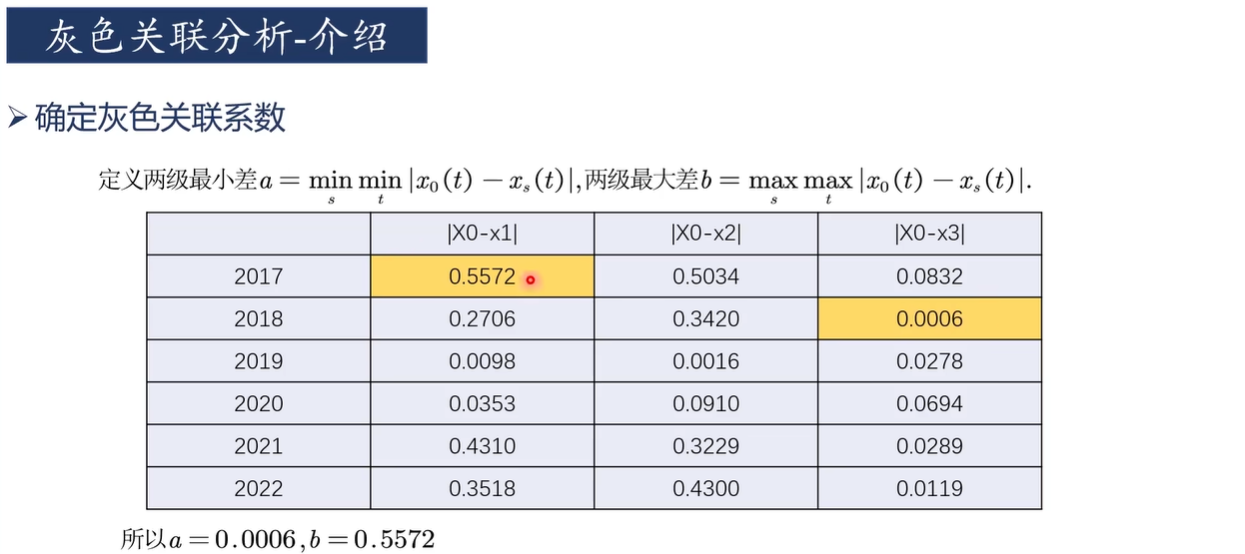
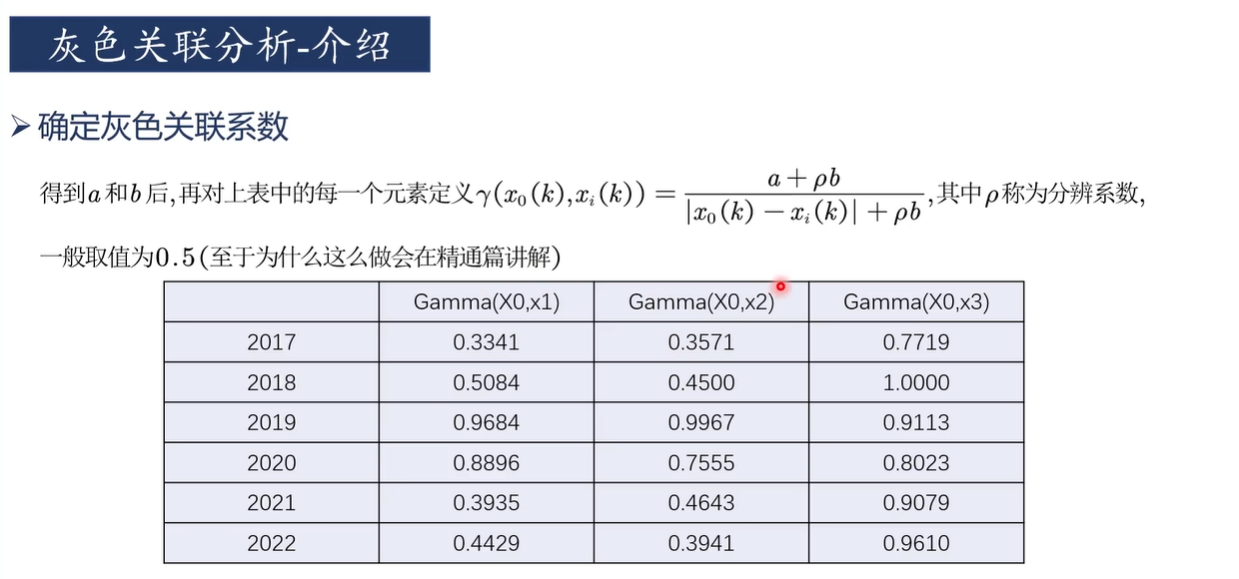
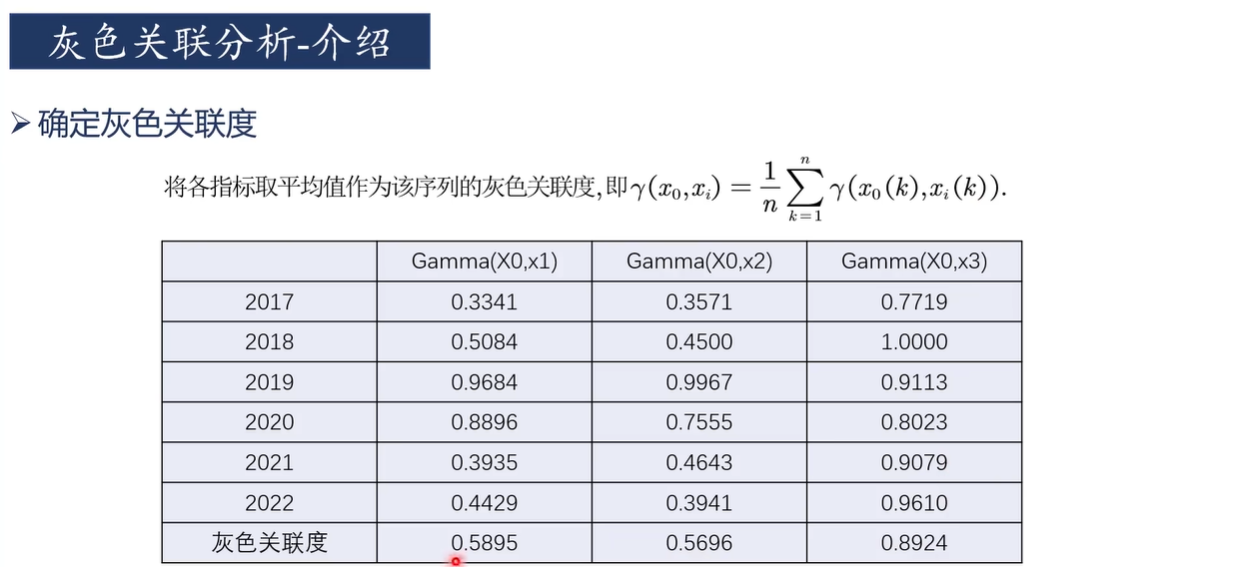
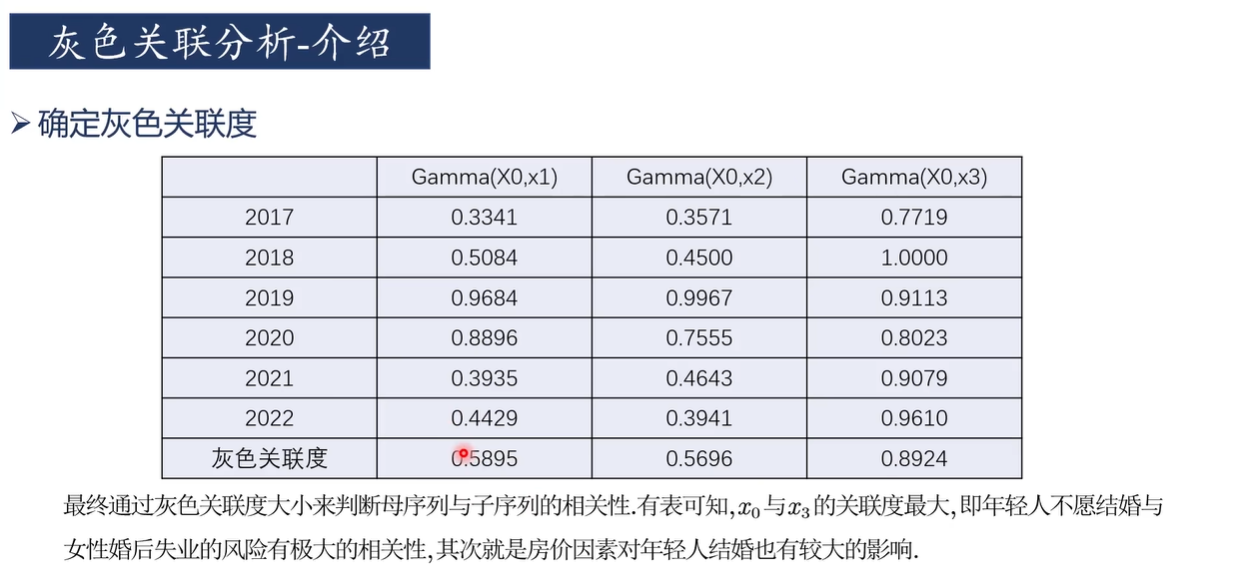
定义


应用
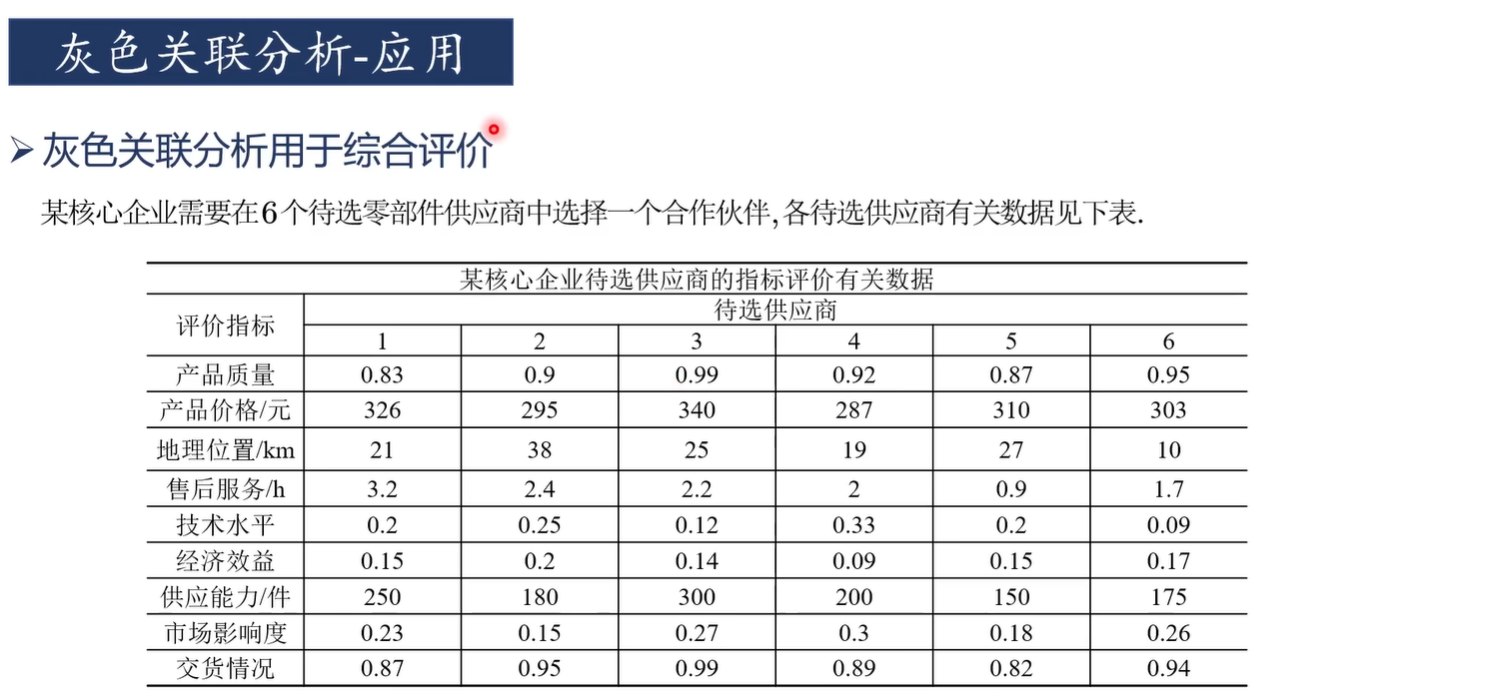
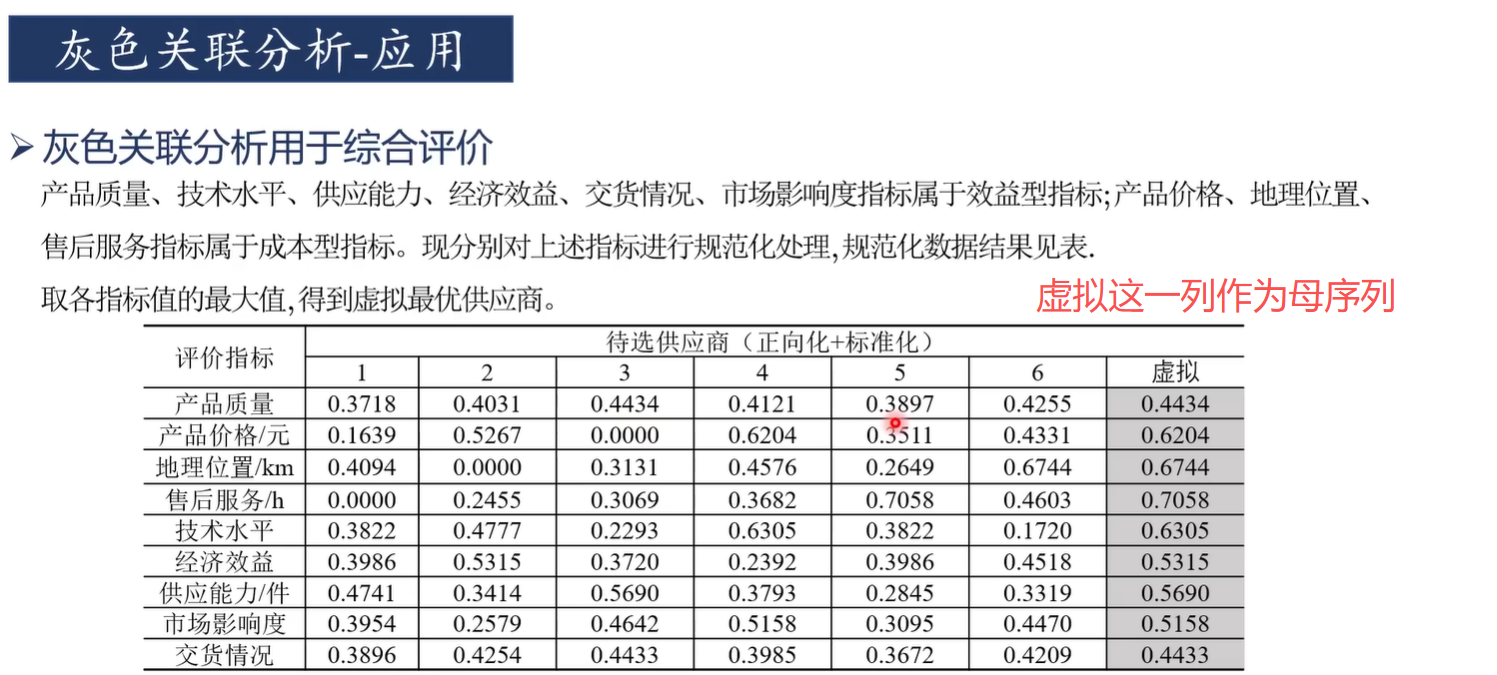
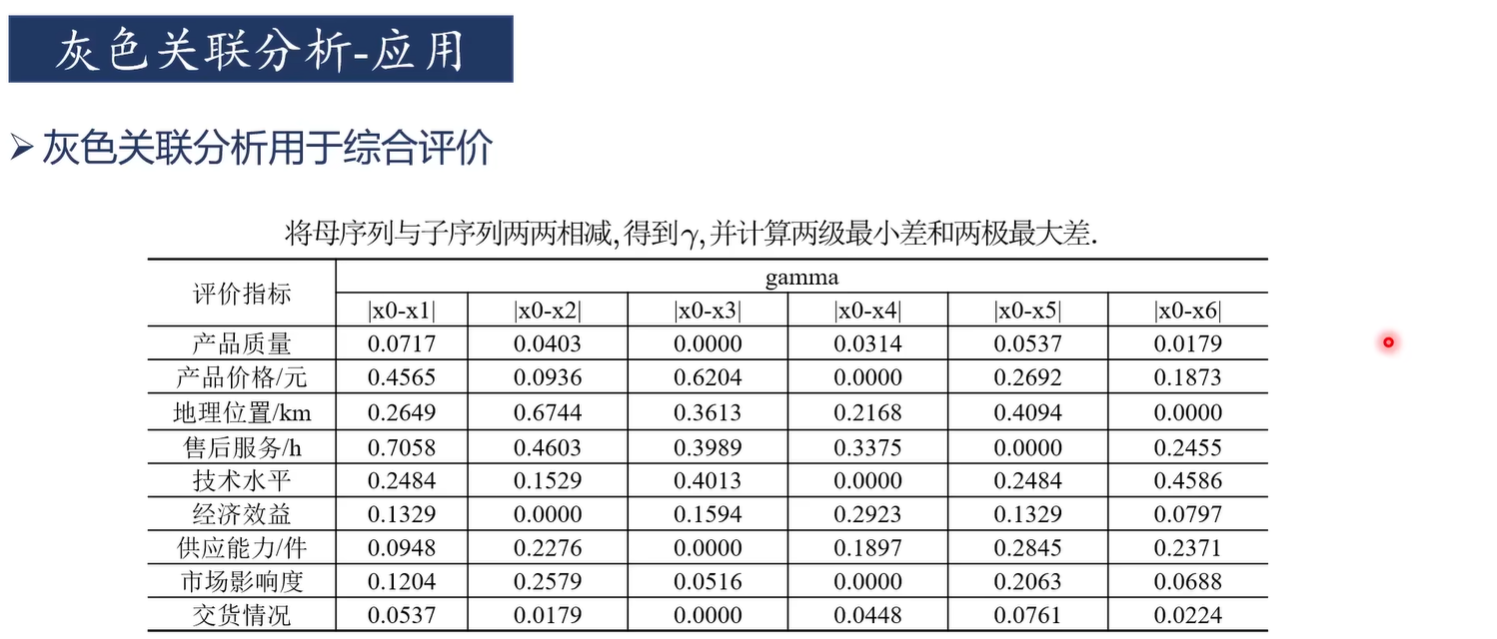
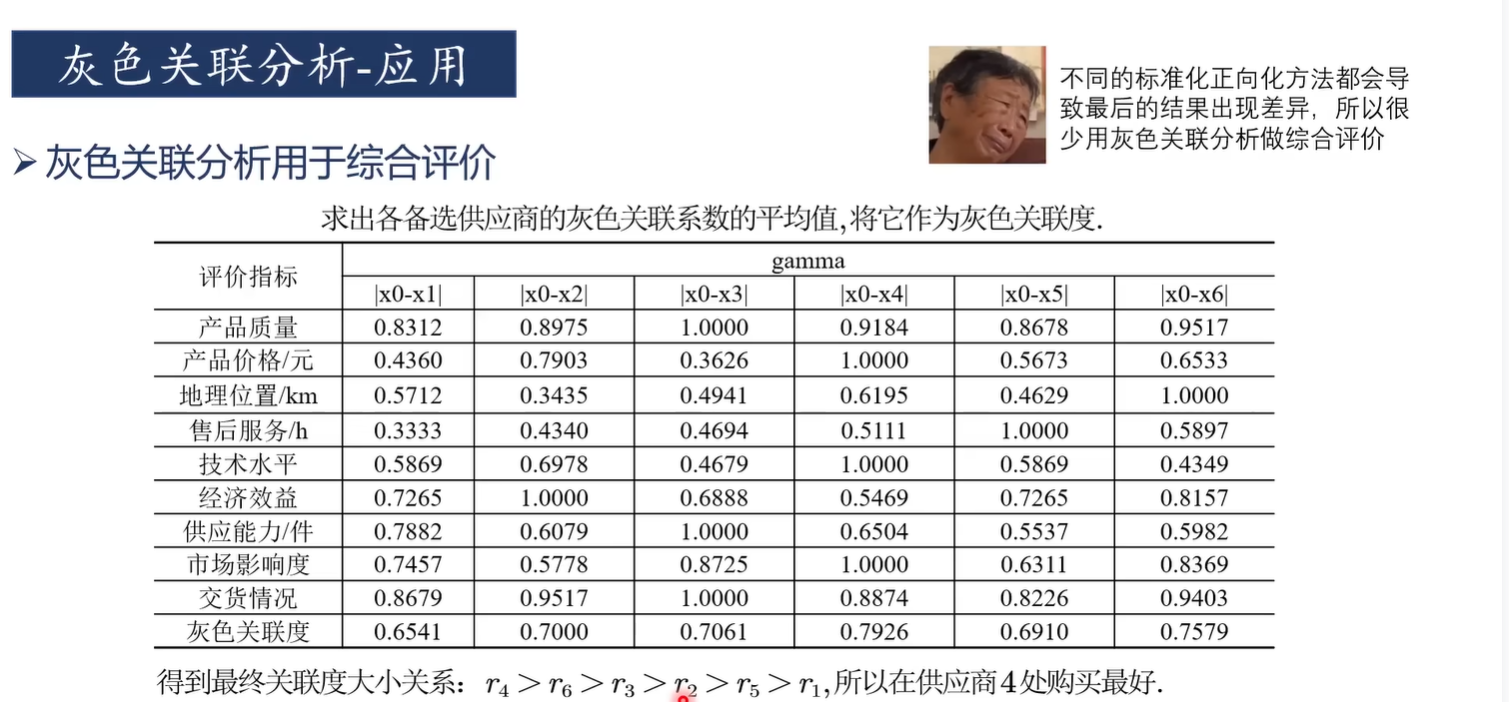
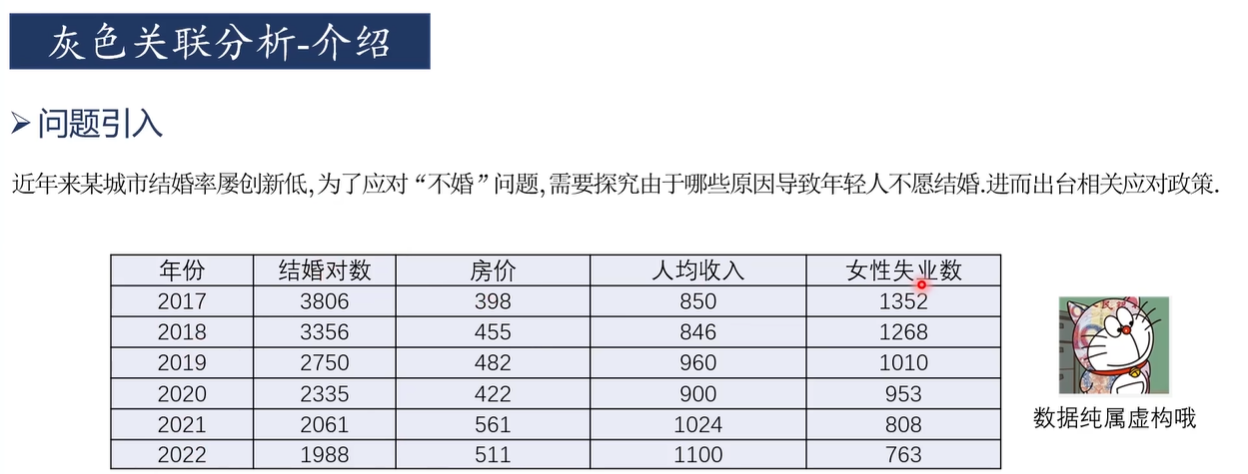
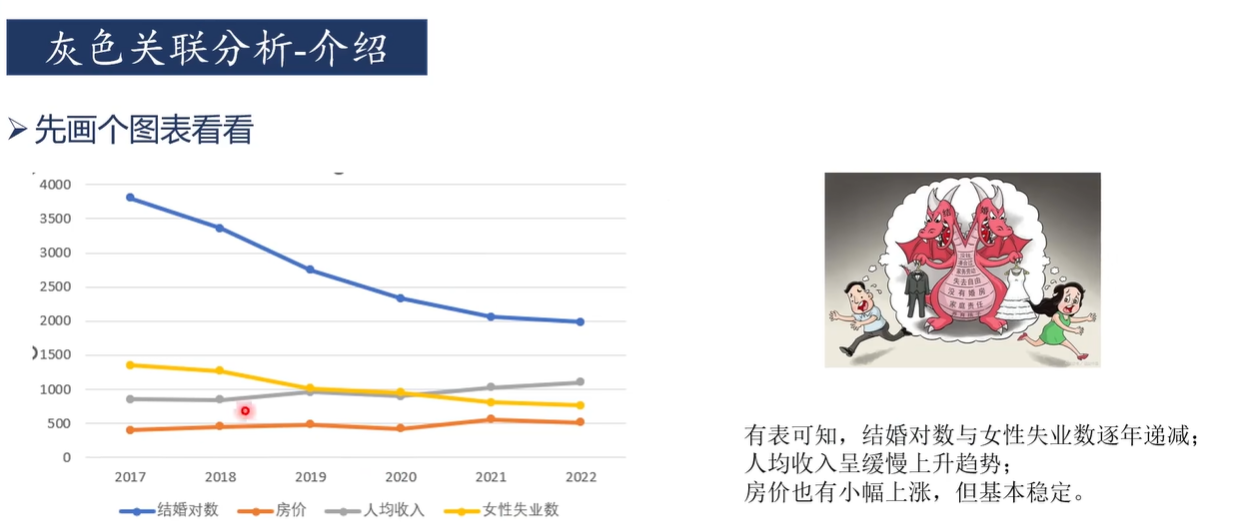
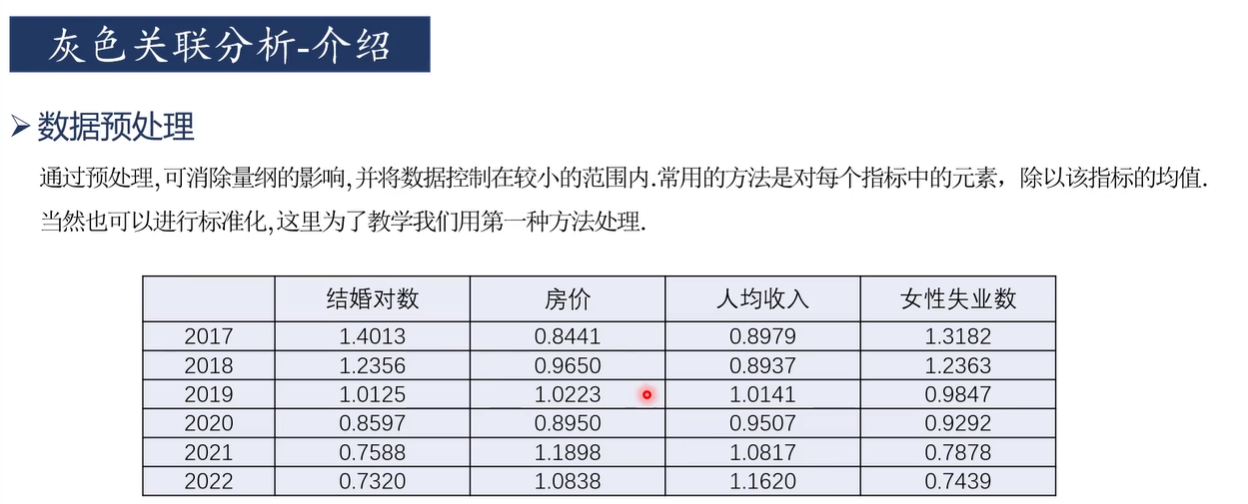
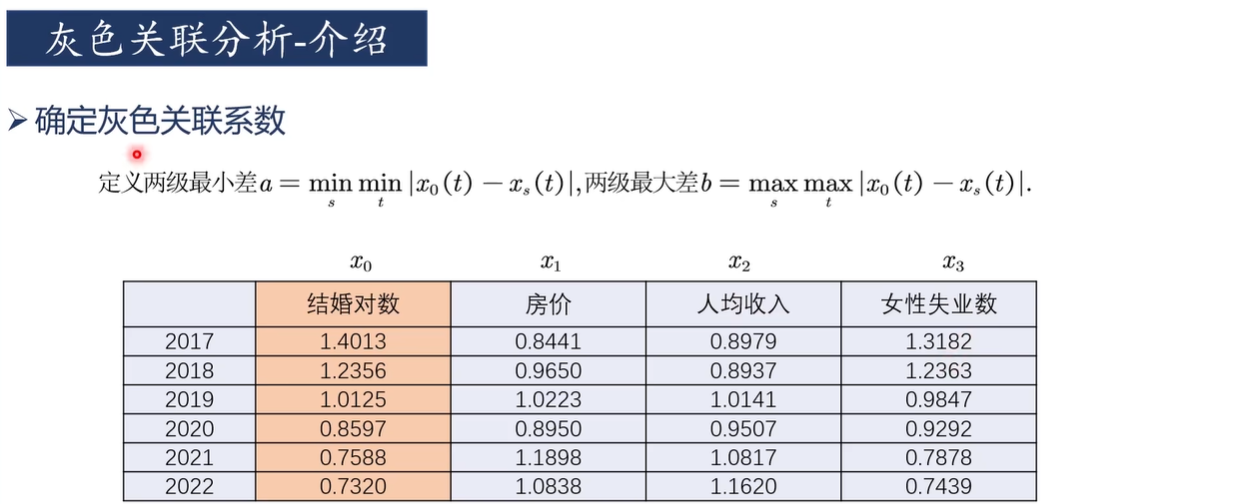
灰色关联分析适合于判断"对于因变量而言,哪些自变量是主要因素,哪些自变量是次要因素"
3-基于excel表格实现灰色关联分析
1)写入数据
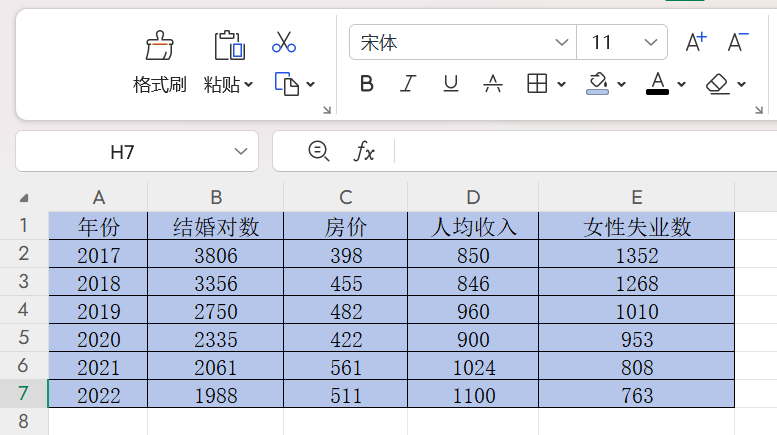
2)数据预处理
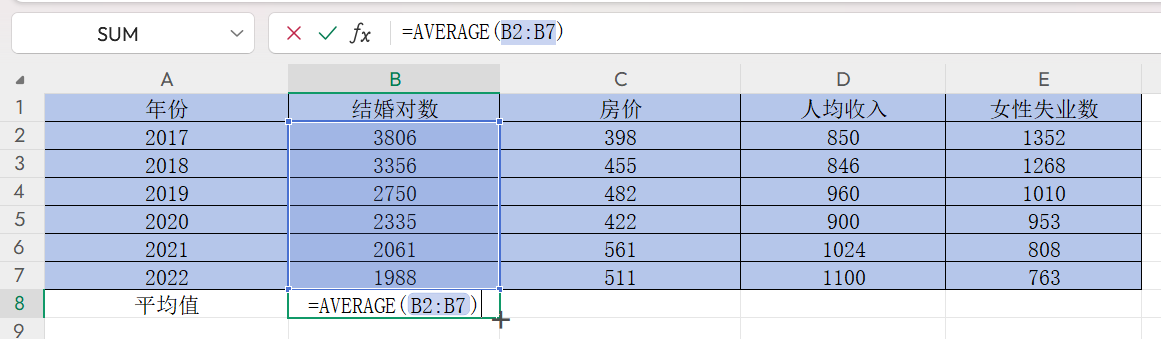
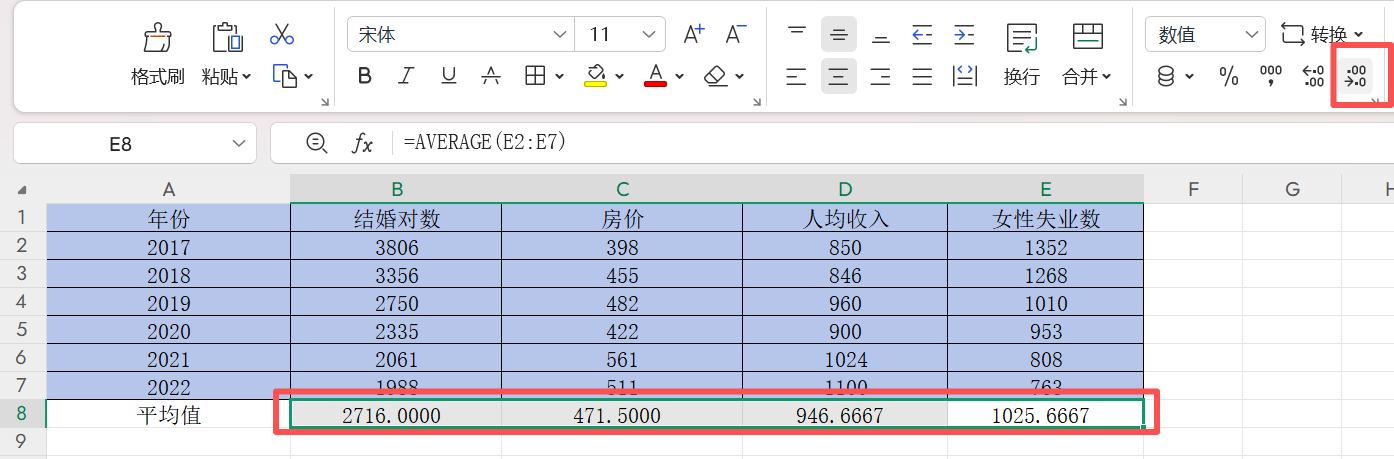
第一步,先求出平均值
在B8单元格双击输入“=”,输入求平均数公式AVERAGE,选中B2:B7并回车得到结婚对数平均值
然后点击右下角的黑色“+”,往右边拖到E8,按回车,即可获得另外三列的平均值,如下
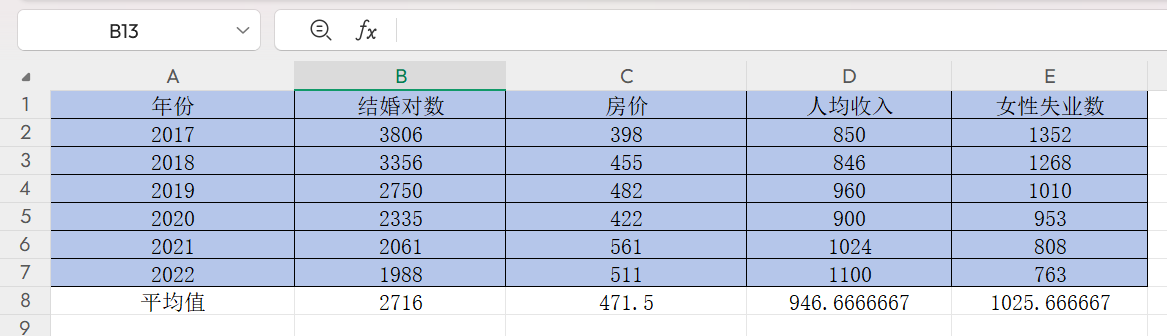
可以点击下面这个地方,改变小数位数
这里我们选中B8,C8,D8,E8,点击![]() 2次,使小数点后面只有4位小数
2次,使小数点后面只有4位小数
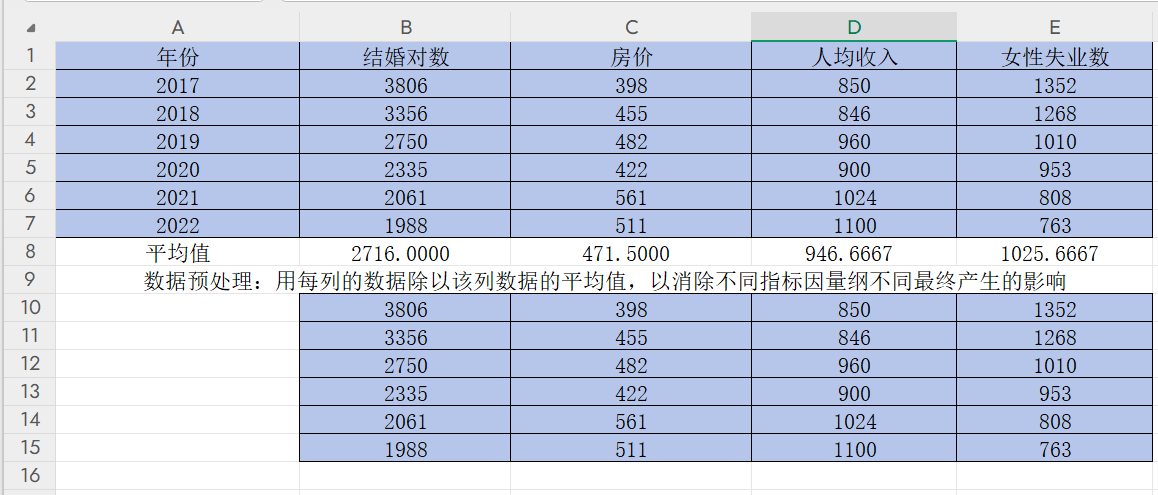
第二步,用每列的数据除以该列数据的平均值,以消除不同指标因量纲不同最终产生的影响
先复制一份上述表格数据
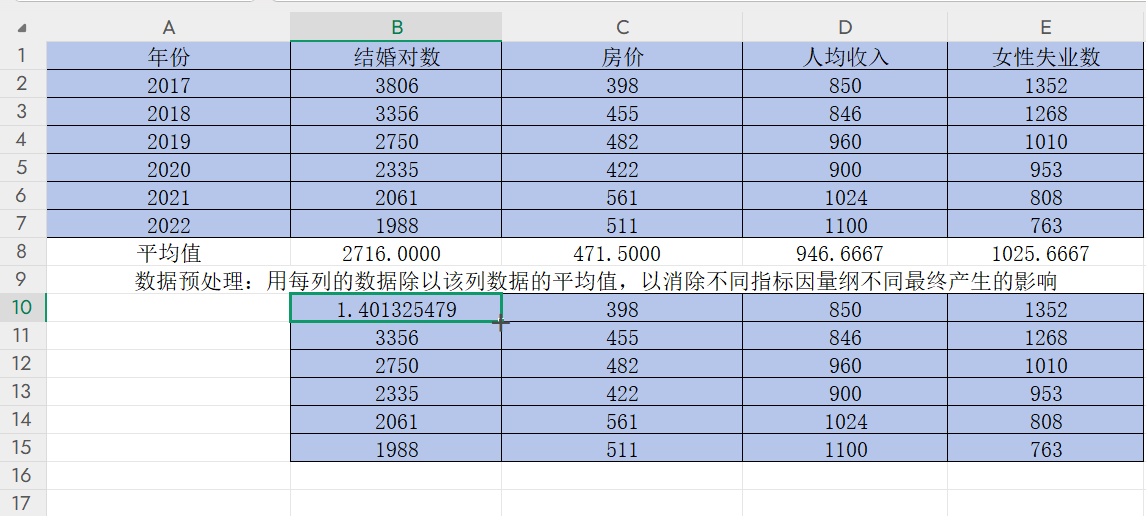
在B10双击单元格输入“=B2/B8”,然后把光标挪到B与8之间,按F4将分母B8(平均值)固定住
回车得到B2/B8的值
按住B10右下角的“+”并往下拉,得到该列其他数据除以平均值后的结果
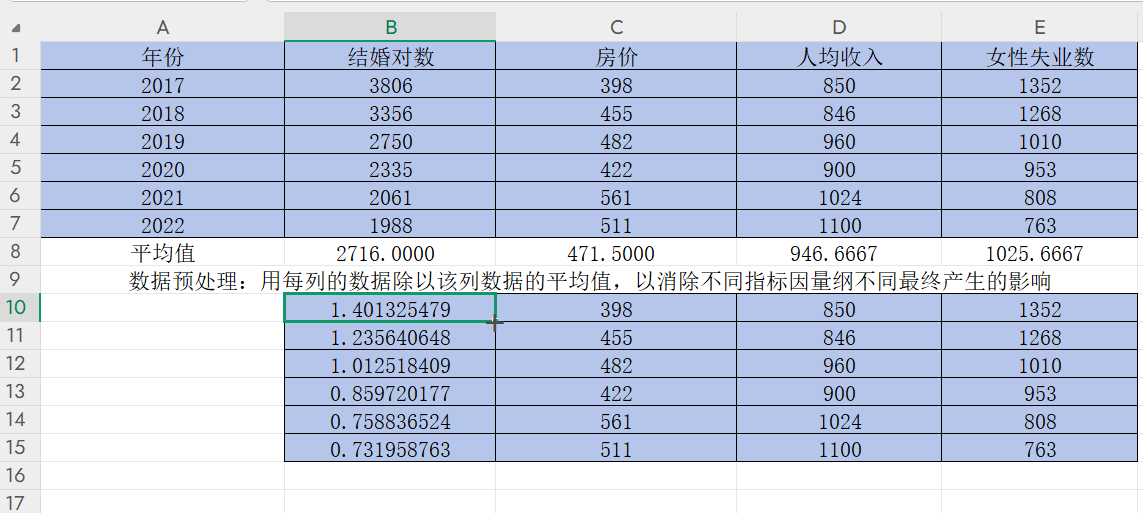
按住B10:B15每个单元格右下角的“+”并往右拉
可以得到该年份其他指标数据除以该指标平均值后的结果
