线性回归的学习
一、线性回归核心定义与目标
线性回归是一种通过属性的线性组合实现预测的线性模型,核心目标是找到一条直线(二维)、一个平面(三维)或更高维的超平面,使模型预测值与真实值的误差最小化。
1. 基础形式(以二维为例)
针对 “房屋大小 - 价格” 这类单特征场景,模型表达式为:
f(x) = W₀ + W₁x
其中,x 为房屋大小(特征),W₀ 为截距,W₁ 为特征系数,f(x) 为预测价格。
2. 一般形式(多特征场景)
对于由 d 个属性描述的样本 x = (x₁; x₂; ⋅⋅⋅; x_d)(x_i 为样本在第 i 个属性的取值),线性模型的通用表达式为:
展开式:f(x) = w₁x₁ + w₂x₂ + ... + w_dx_d + b
向量形式:f(x) = w^T x + b
其中,w = (w₁; w₂; ⋅⋅⋅; w_d) 为特征系数向量,b 为截距,w^T 表示 w 的转置。
二、线性回归的求解方法:最小二乘法
1. 核心原理
均方误差对应 “欧氏距离”,基于均方误差最小化求解模型参数的方法称为 “最小二乘法”。其本质是找到一条直线(或超平面),使所有样本到该直线(或超平面)的欧氏距离之和最小。
2. 参数估计过程
定义损失函数 E(w,b):衡量预测值与真实值的误差,表达式为所有样本误差的平方和:
E(w,b) = Σ(从i=1到m)[y_i - (w x_i + b)]²
其中,m 为样本数量,y_i 为第 i 个样本的真实值,w x_i + b 为第 i 个样本的预测值。
参数求解目标:找到最优的 w(系数)和 b(截距),使 E(w,b) 最小化,即:
(w^, b^) = argmin(w,b)E(w,b)
求解方式:对 E(w,b) 分别关于 w 和 b 求导,令导数为 0,可得到最优参数的解析解:
系数 w:w = [Σ(从i=1到m)(x_i - x̄)(y_i - ȳ)] / [Σ(从i=1到m)(x_i - x̄)²](x̄ 为样本特征均值,ȳ 为样本真实值均值)
截距 b:b = ȳ - w x̄
三、线性回归的核心评估指标
PPT 中重点介绍了 3 类评估指标,用于衡量模型拟合效果,具体如下:
1. 误差平方和 / 残差平方和(SSE/RSS)
定义:所有样本 “真实值 - 预测值” 的平方总和,反映模型整体误差大小。
公式:SSE = Σ(从i=1到m)(y_i - ŷ_i)²(ŷ_i 为第 i 个样本的预测值)
特点:值越小,模型误差越小;但受样本数量影响,无法直接横向对比不同样本量的模型。
2. 平方损失 / 均方误差(MSE)
定义:SSE 的平均值,消除了样本数量对误差的影响,是回归任务中最常用的指标之一。
公式:MSE = (1/m) * Σ(从i=1到m)(y_i - ŷ_i)²
特点:值越小,模型拟合效果越好;单位为 “目标变量单位的平方”(如房价预测中,单位为 “美元 ²”)。
3. 决定系数(R²)
定义:衡量模型对数据变异的解释能力,取值范围为 (-∞, 1],越接近 1,模型拟合效果越好。
核心逻辑:通过对比 “模型误差” 与 “真实值自身波动” 的比例来评估拟合度,公式有两种等价形式:
形式 1(基于平方和):R² = 1 - (SSE / SST)
形式 2(基于 MSE 和方差):R² = 1 - (MSE / Var(y))
其中,SST = Σ(从i=1到m)(y_i - ȳ)²(真实值与均值的平方和,即总平方和),Var(y) 为真实值的方差。
示例:PPT 中给出的拟合案例(y = 1.595x + 0.2321),R² = 0.9322,说明模型能解释 93.22% 的数据变异,拟合效果优秀。
四、多元线性回归
当样本包含多个特征时,线性回归扩展为 “多元线性回归”,核心逻辑与单特征一致,但模型形式和参数维度更复杂。
1. 模型表达式
对于包含 n 个特征的样本,预测公式为:
ŷ = w₀ + w₁x₁ + w₂x₂ + ... + w_nx_n
其中,w₀ 为截距,w₁~w_n 为各特征的系数,x₁~x_n 为样本的各特征取值。
2. 矩阵形式(便于计算)
将 m 个样本的特征组织为特征矩阵 X(m 行 n 列,每行对应一个样本,每列对应一个特征),参数组织为系数向量 w(n+1 维,包含 w₀ 截距),则模型可表示为:
Ŷ = X w
其中,Ŷ 为 m 个样本的预测值向量(m 维)。
五、课堂练习:线性回归实践(波士顿房价预测)
PPT 以 “波士顿房价预测” 为例,给出了基于 scikit-learn 库的线性回归实践方向,核心内容如下:
1. 核心 API
使用 sklearn.linear_model.LinearRegression() 类实现线性回归,关键参数说明:
fit_intercept:布尔值,是否包含截距(b),默认 True(若设为 False,模型直线过原点)。
normalize:布尔值,是否对输入数据做归一化处理,默认 False(若需归一化,建议先使用 StandardScaler 预处理)。
2. 实践目标
通过加载波士顿房价数据集(注:因伦理问题,sklearn 1.2+ 版本已移除 load_boston,需用加州房价数据集等替代),构建线性回归模型,预测房价并通过 MSE、R² 等指标评估模型效果。
六、总结
本次主要围绕线性回归的 “定义 - 求解 - 评估 - 扩展 - 实践” 展开,核心逻辑可概括为:
- 线性回归通过线性组合特征实现预测,目标是最小化误差;
- 最小二乘法是求解线性回归参数的核心方法,通过求导得到最优解析解;
- 评估模型需结合 SSE(整体误差)、MSE(平均误差)、R²(解释能力),其中 R² 是最直观的拟合效果指标;
- 多元线性回归是单特征场景的扩展,通过矩阵形式简化多特征计算;
- 实践中可基于 scikit-learn 快速实现,需注意参数设置(如是否包含截距)和数据集选择。
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.datasets import fetch_california_housing # 替换为加州房价数据集
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error, r2_score
from sklearn.preprocessing import StandardScaler
import matplotlib
# 强制使用Tkinter后端,这是最稳定的选择之一
matplotlib.use('TkAgg', force=True)# 中文显示配置
plt.rcParams["font.family"] = ["SimHei", "WenQuanYi Micro Hei", "Heiti TC"]
plt.rcParams["axes.unicode_minus"] = False# 加载加州房价数据集
california = fetch_california_housing()
X = california.data # 特征数据
y = california.target # 房价数据(单位:10万美元)# 数据集划分
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42
)# 数据标准化
scaler = StandardScaler()
X_train_scaled = scaler.fit_transform(X_train)
X_test_scaled = scaler.transform(X_test)# 创建并训练线性回归模型
model = LinearRegression()
model.fit(X_train_scaled, y_train)# 模型预测
y_pred = model.predict(X_test_scaled)# 模型评估
mse = mean_squared_error(y_test, y_pred)
rmse = np.sqrt(mse)
r2 = r2_score(y_test, y_pred)print(f"均方误差 (MSE): {mse:.4f}")
print(f"均方根误差 (RMSE): {rmse:.4f}") # 单位:10万美元
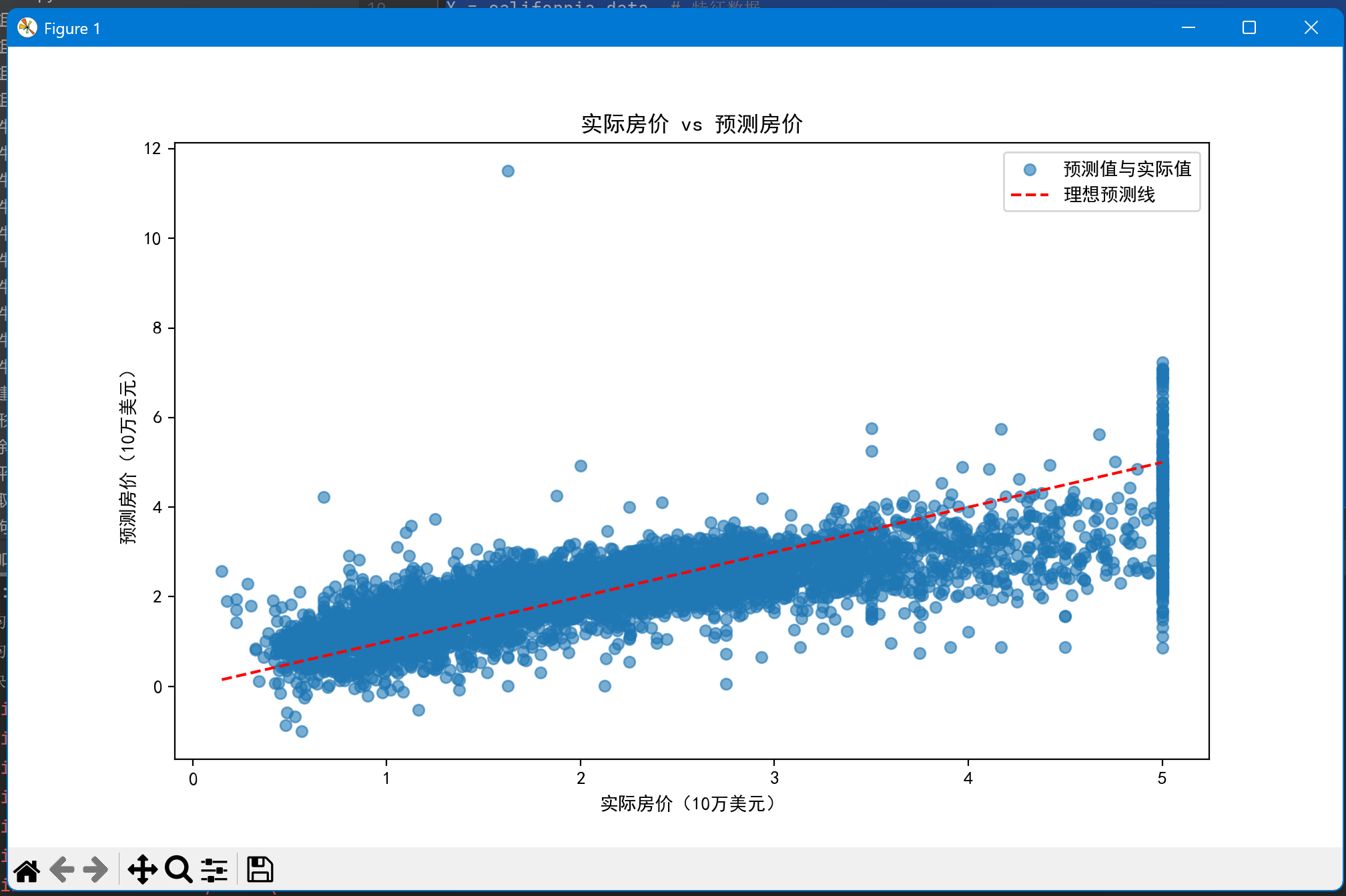
print(f"决定系数 (R²): {r2:.4f}")# 可视化预测结果
plt.figure(figsize=(10, 6))
plt.scatter(y_test, y_pred, alpha=0.6, label='预测值与实际值')
plt.plot([y.min(), y.max()], [y.min(), y.max()], 'r--', label='理想预测线')
plt.xlabel('实际房价(10万美元)')
plt.ylabel('预测房价(10万美元)')
plt.title('实际房价 vs 预测房价')
plt.legend()
plt.show()
因为波士顿与现在版本不兼容,所以用加州房价预测来代替波士顿。