递归思路:从DFS到二叉树直径的实战(通俗易懂)
对递归的思考

最近做了很多关于递归实现dfs的题,一直在想什么时候总结一下递归使用时的关键点,但一直没想好就拖得没影了,写完上面的总结时,突然想到一句话“种一棵树最好的时间点是十年前,其次就是现在”,那这次就借这篇博客总结一下我对递归的思考
先简单讲一下我对递归的理解,递归解决问题的核心思路就是:将一个大问题转换为许多个与这个大问题处理逻辑相同的小问题,最后只用写出处理小问题的逻辑代码,再进行递归调用即可!
说着简单,想着也很简单,但真正解决问题时想理清思路还需要大量的题目积累与锻炼,这里再总结一下递归使用时的关键点
①问题分解(核心底层逻辑)
②递归时机(与底层逻辑相关)
③边界条件(递归停止时机)
④递归参数与递归结果(合理利用返回值)
纸上得来终觉浅,绝知此事要躬行,我们就拿下面的题结合前面的所讲深入感受递归
问题描述
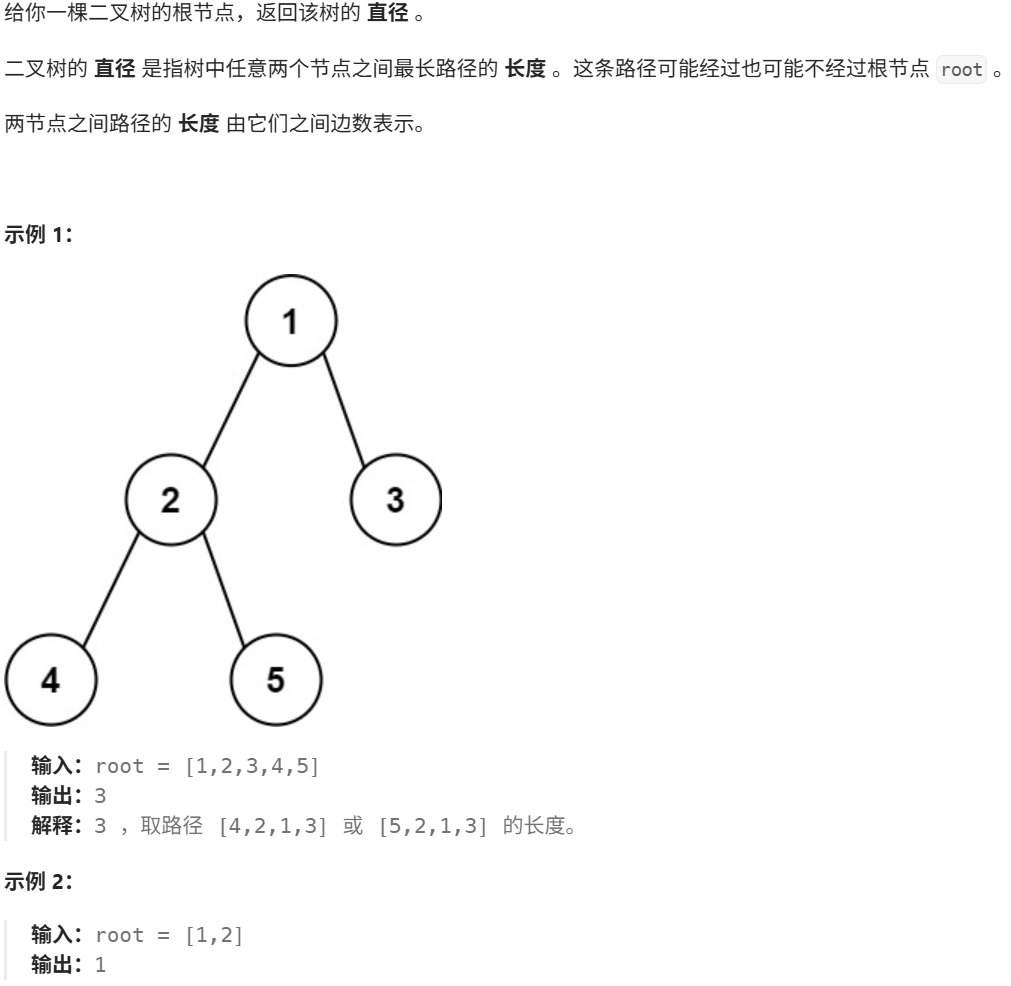
解题思路
关键点在于:二叉树的最长路径不一定经过根节点!它可能隐藏在任意子树中。结合递归的四要素我们需要理清:
①问题分解(核心底层逻辑):计算当前节点左子树深度与右子树深度之和
②递归时机(与底层逻辑相关):节点不为非空节点(说明该节点还可能再往下延伸)
③边界条件(递归停止时机):节点为空节点(说明左/右子树已到达最深)
④递归参数与递归结果(合理利用返回值):使用成员变量记录直径最大值
代码实现
class Solution {public int max=0;public int diameterOfBinaryTree(TreeNode root) {if(root==null){return 0;}max=0;int result=jisuan(root);return max;}private int jisuan(TreeNode root) {if(root==null){return 0;}int left=jisuan(root.left);int right=jisuan(root.right);max=Math.max(max,left+right);return Math.max(left,right)+1;}
}算法解析
- 递归终止条件:遇到空节点时返回深度0
- 后序遍历框架:先递归处理左右子树,再处理当前节点
- 核心操作:
- 将
左子树深度 + 右子树深度与全局最大值比较 - 返回当前子树深度(左右子树深度较大值 + 1)
- 将
- 时间复杂度:O(N),每个节点仅访问一次
- 空间复杂度:O(H),递归栈深度等于树高
关键点说明
- 为什么需要全局变量:最长路径可能出现在任意子树中,必须全局记录
- 深度计算原理:每个节点的深度由其最深子树决定
- 路径计算本质:路径长度等于连接边的数量(非节点数)
总结
至此,相信大家对递归有了更加系统的认识
这个解法巧妙地利用DFS后序遍历:
- 自底向上计算每个节点的子树深度
- 在递归过程中动态更新最大直径
- 仅用O(1)额外空间存储全局最大值

