数据结构 -- 树
一、树的基本概念
(一)定义
树是由 n(n ≥ 0) 个结点组成的有限集合,是一种非线性层次结构:
- 当
n = 0时,称为空树; - 当
n > 0时,存在唯一的根结点(无前驱结点),其余结点可划分为m(m ≥ 0)个互不相交的有限子集,每个子集都是一棵独立的子树。
(二)结点与树的核心属性
| 概念 | 定义 |
|---|---|
| 结点的度 | 结点拥有的子树个数 |
| 叶结点(终端结点) | 度为 0 的结点(无子树,位于树的最底层) |
| 分支结点(非终端结点) | 度不为 0 的结点(至少拥有一棵子树) |
| 树的度 | 树中所有结点的最大度数 |
| 深度 / 高度 | 从根结点开始计数,根为第 1 层,子结点依次递增,树的最大层数即为深度 / 高度 |
(三)存储结构
- 顺序存储:通过数组存储结点,需结合结点间的层次关系(如双亲下标)关联数据,适用于结构规则的树(如完全二叉树)。
- 链式存储:通过指针记录结点的子树地址(如孩子指针、兄弟指针),灵活性高,适用于各类形态的树。
二、二叉树的基本概念
(一)定义
二叉树是 n(n ≥ 0) 个结点的有限集合,满足:
- 当
n = 0时,为空二叉树; - 当
n > 0时,由根结点、左子树和右子树组成,且左、右子树互不相交,均为二叉树。
(二)核心特点
- 每个结点最多有 2 棵子树(左子树和右子树),即二叉树的度最大为 2;
- 左、右子树具有有序性,不可随意颠倒(如 “仅有左子树” 与 “仅有右子树” 是两种不同结构);
- 若结点仅有一棵子树,必须明确标注是左子树还是右子树。
三、特殊二叉树
| 类型 | 定义 |
|---|---|
| 斜树 | 所有结点仅含一棵子树,分为左斜树(仅左子树)和右斜树(仅右子树) |
| 满二叉树 | 深度为 k(k ≥ 1),所有分支结点均有左、右子树,且所有叶子结点在同一层 |
| 完全二叉树 | 深度为 k(k ≥ 1),按层序编号后,与同深度满二叉树的结点编号完全一致 |
四、二叉树重要性质
- 第
i层结点数上限:第i(i ≥ 1)层最多有2^{i-1}个结点(如第 3 层最多 4 个结点); - 深度为
k的结点总数上限:深度为k(k ≥ 1)的二叉树,最多有2^k - 1个结点(此时为满二叉树); - 叶子结点与度为 2 的结点关系:任意非空二叉树中,叶子结点数
n₀= 度为 2 的结点数n₂+ 1(即n₀ = n₂ + 1); - 完全二叉树深度计算:含
n个结点的完全二叉树,深度为⌊log₂n⌋ + 1(⌊x⌋表示向下取整)。
五、二叉树遍历方式
二叉树遍历是按规则访问所有结点(每个结点仅访问一次),核心分为深度优先遍历(DFS)和广度优先遍历(BFS):
| 遍历类型 | 具体方式 | 遍历顺序 |
|---|---|---|
| 深度优先遍历 | 前序遍历 | 根结点 → 左子树 → 右子树 |
| 中序遍历 | 左子树 → 根结点 → 右子树 | |
| 后序遍历 | 左子树 → 右子树 → 根结点 | |
| 广度优先遍历 | 层序遍历 | 按层次从上到下、同层从左到右 |
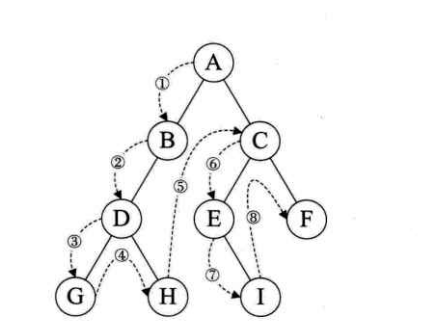
前序遍历
规则是若二叉树为空,则空操作返回,否则先访问根结点,然后前序遍历左子
树,再前序遍历右子树。如图,遍历的顺序为:ABDGHCEIF。
void PreOrder(TreeNode* root) {if (root == NULL) return; // 空树,递归终止printf("%d ", root->data); // 访问根结点PreOrder(root->left); // 递归遍历左子树PreOrder(root->right); // 递归遍历右子树
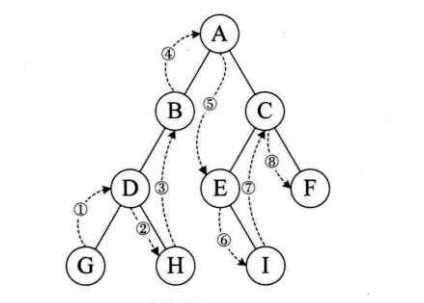
}中序遍历
规则是若树为空,则空操作返回,否则从根结点开始(注意并不是先访问根结
点),中序遍历根结点的左子树,然后是访问根结点,最后中序遍历右子树。如图,遍历的顺序为:GDHBAEICF。
void InOrder(TreeNode* root) {if (root == NULL) return; // 空树,递归终止InOrder(root->left); // 递归遍历左子树printf("%d ", root->data); // 访问根结点InOrder(root->right); // 递归遍历右子树
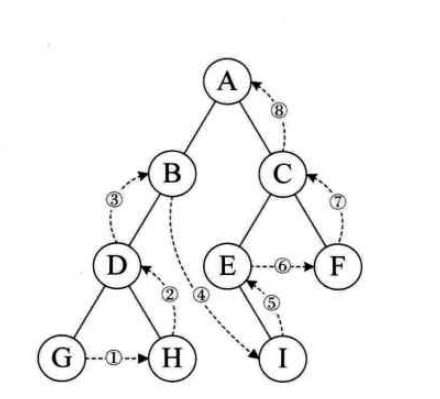
}3.后序遍历
规则是若树为空,则空操作返回,否则从左到右先叶子后结点的方式遍历访问左
右子树,最后是访问根结点。如图,遍历的顺序为:GHDBIEFCA。
void PostOrder(TreeNode* root) {if (root == NULL) return; // 空树,递归终止PostOrder(root->left); // 递归遍历左子树PostOrder(root->right); // 递归遍历右子树printf("%d ", root->data); // 访问根结点
}遍历顺序:按树的层次从上到下、同一层从左到右依次访问所有结点,本质是 “按层访问”。实现依赖:需借助队列(先进先出,FIFO),通过 “根结点入队 → 队头出队访问 → 左右子结点入队 → 循环至队空” 的逻辑实现。
void LevelOrder(TreeNode* root) {if (root == NULL) return; // 空树,直接返回SeqQue* queue = CreateSeqQue(100); // 创建容量为 100 的队列EnterSeqQue(queue, root); // 根结点入队while (!IsEmptySeqQue(queue)) { // 队列非空,循环处理TreeNode* curr = GetHeadSeqQue(queue); // 取队头结点printf("%d ", curr->data); // 访问当前结点QuitSeqQue(queue); // 队头结点出队if (curr->left != NULL) // 左子结点非空,入队EnterSeqQue(queue, curr->left);if (curr->right != NULL) // 右子结点非空,入队EnterSeqQue(queue, curr->right);}DestroySeqQue(queue); // 销毁队列,释放内存
}