线性回归:机器学习中的基础建模工具
在机器学习领域,线性回归是一种经典且应用广泛的模型。它以直观的原理、清晰的可解释性和高效的计算性能,成为数据科学入门者的必备知识,也是解决回归问题的常用工具。
一、线性回归的核心逻辑:找到最佳拟合关系
线性回归的本质是通过属性的线性组合构建预测模型,目标是找到一条直线(或高维空间的超平面),使预测值与真实值的误差最小化。
- 简单线性回归:当仅用一个特征预测目标变量时,模型形式为 f(x) = w₀ + w₁x。例如用房屋大小(x)预测房价(f (x)),其中 w₀是截距,w₁是特征系数。
- 一般形式:对于含 d 个特征的样本 x=(x₁, x₂,...,x_d),线性模型可表示为 f(x) = w₁x₁ + w₂x₂ + ... + w_dx_d + b,向量形式简化为 f(x) = wᵀx + b(w 为权重向量,b 为偏置项)。
无论是哪种形式,核心都是通过求解参数(w 和 b),建立特征与目标变量的线性关系。
二、参数求解:最小二乘法的应用
如何确定最优的参数 w 和 b?线性回归采用最小二乘法,其核心思想是最小化预测值与真实值的均方误差(对应欧氏距离)。
- 目标函数:需最小化的误差平方和为 E(w,b) = Σ(yᵢ - f(xᵢ))²(yᵢ为真实值,f (xᵢ) 为预测值)。
- 求解过程:通过对 E (w,b) 分别求 w 和 b 的偏导,令导数为 0,即可得到参数的最优解(这一过程称为 “参数估计”)。
三、模型评估:如何判断拟合效果?
为衡量模型性能,常用以下指标:
- 误差平方和(SSE/RSS):所有样本预测误差的平方和,SSE = Σ(yᵢ - ŷᵢ)²(ŷᵢ为预测值),值越小说明拟合越好。
- 均方误差(MSE):SSE 的平均值,MSE = (1/n)Σ(yᵢ - ŷᵢ)²,消除了样本数量的影响,便于跨数据集比较。
- R²(决定系数):最常用的指标,取值范围 [0,1],越接近 1 表示模型拟合效果越好。其计算公式为 R² = 1 - (SSE/SST)(SST 为总平方和,即真实值与均值差的平方和)。
四、多元线性回归:处理多特征问题
当目标变量受多个特征影响时(如房价受面积、房间数、地段等影响),需用到多元线性回归,模型形式为 y = w₀ + w₁x₁ + w₂x₂ + ... + wₙxₙ,其中 x₁到 xₙ为特征,w₀到 wₙ为参数。
多元线性回归通过矩阵运算高效求解参数,核心逻辑与简单线性回归一致,均基于最小二乘法最小化误差。
五、实战:用 scikit-learn 实现线性回归
在 Python 中,可通过 scikit-learn 的linear_model.LinearRegression快速实现线性回归,关键参数包括:
- fit_intercept:是否保留截距项(默认 True,若为 False 则模型过原点);
- normalize:是否归一化数据(默认 False)。
以波士顿房价预测为例,流程如下:


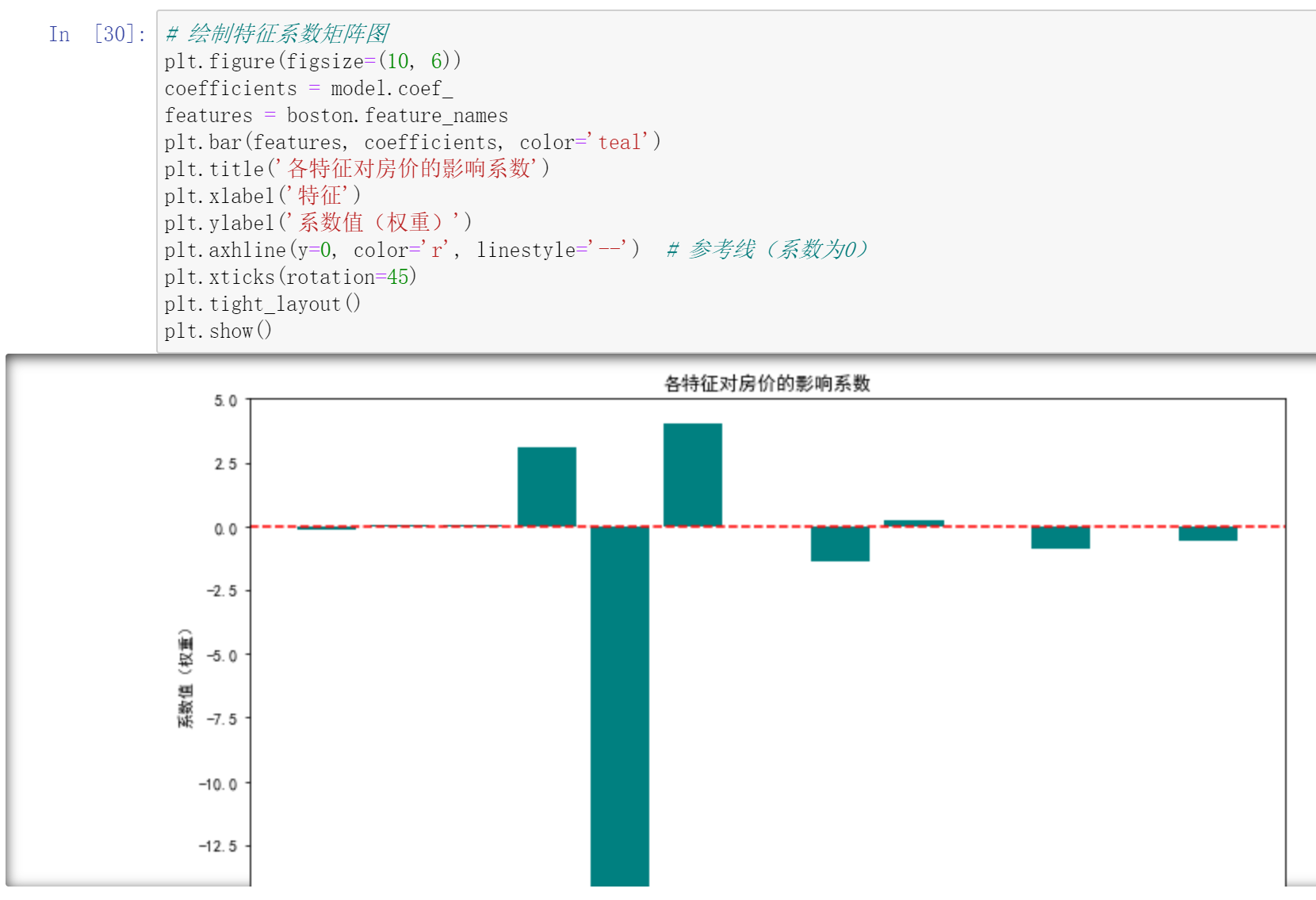
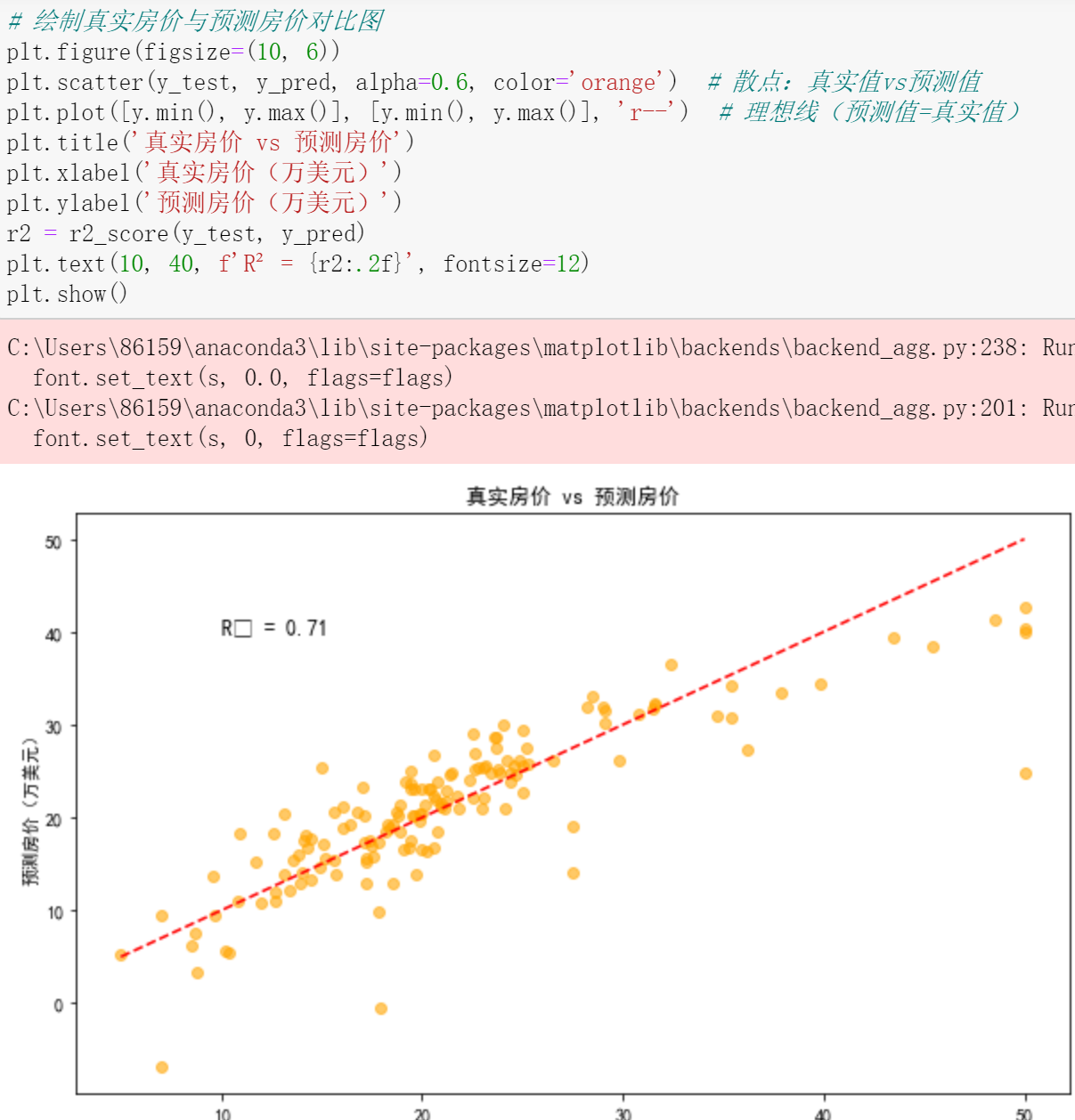
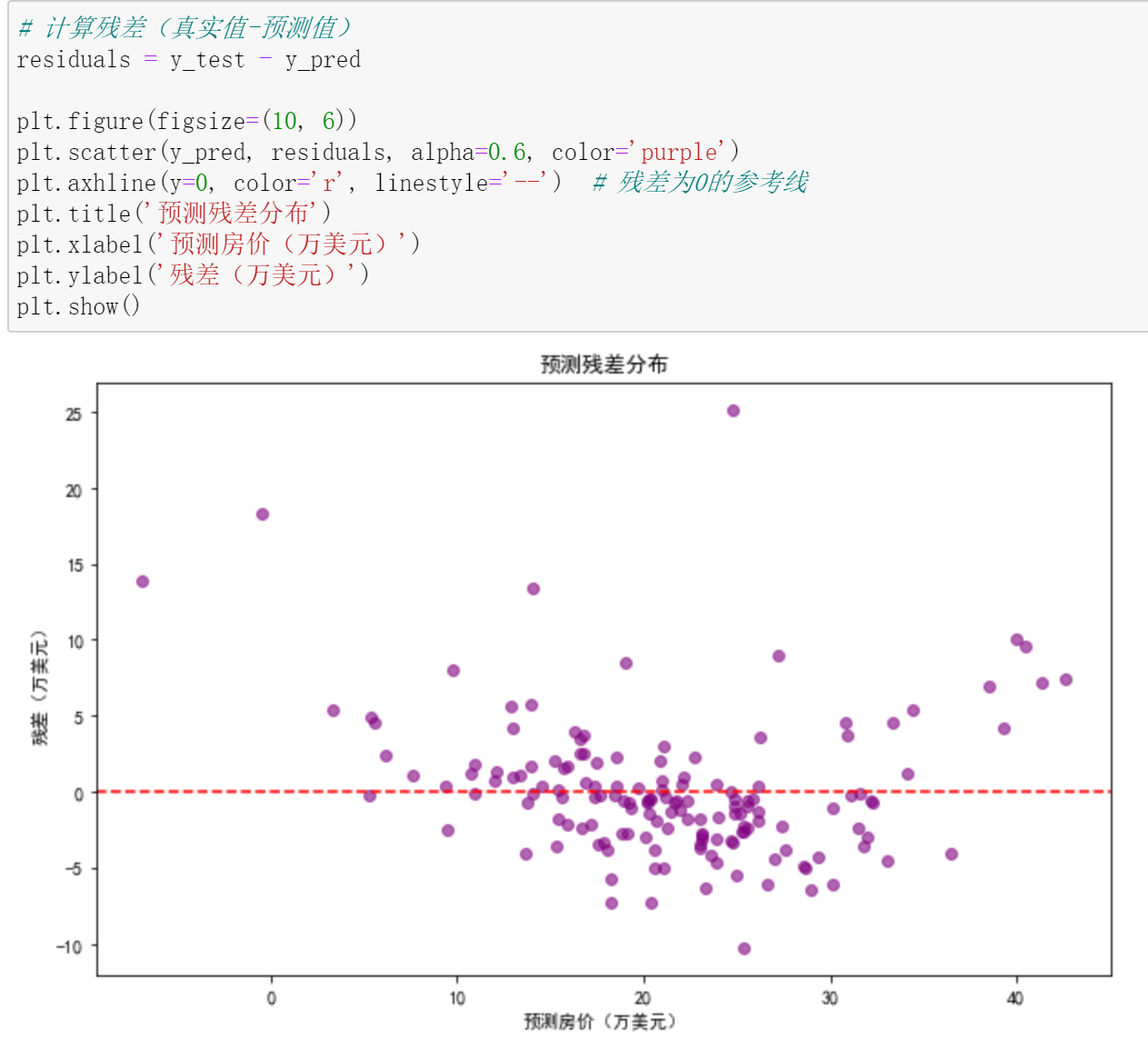
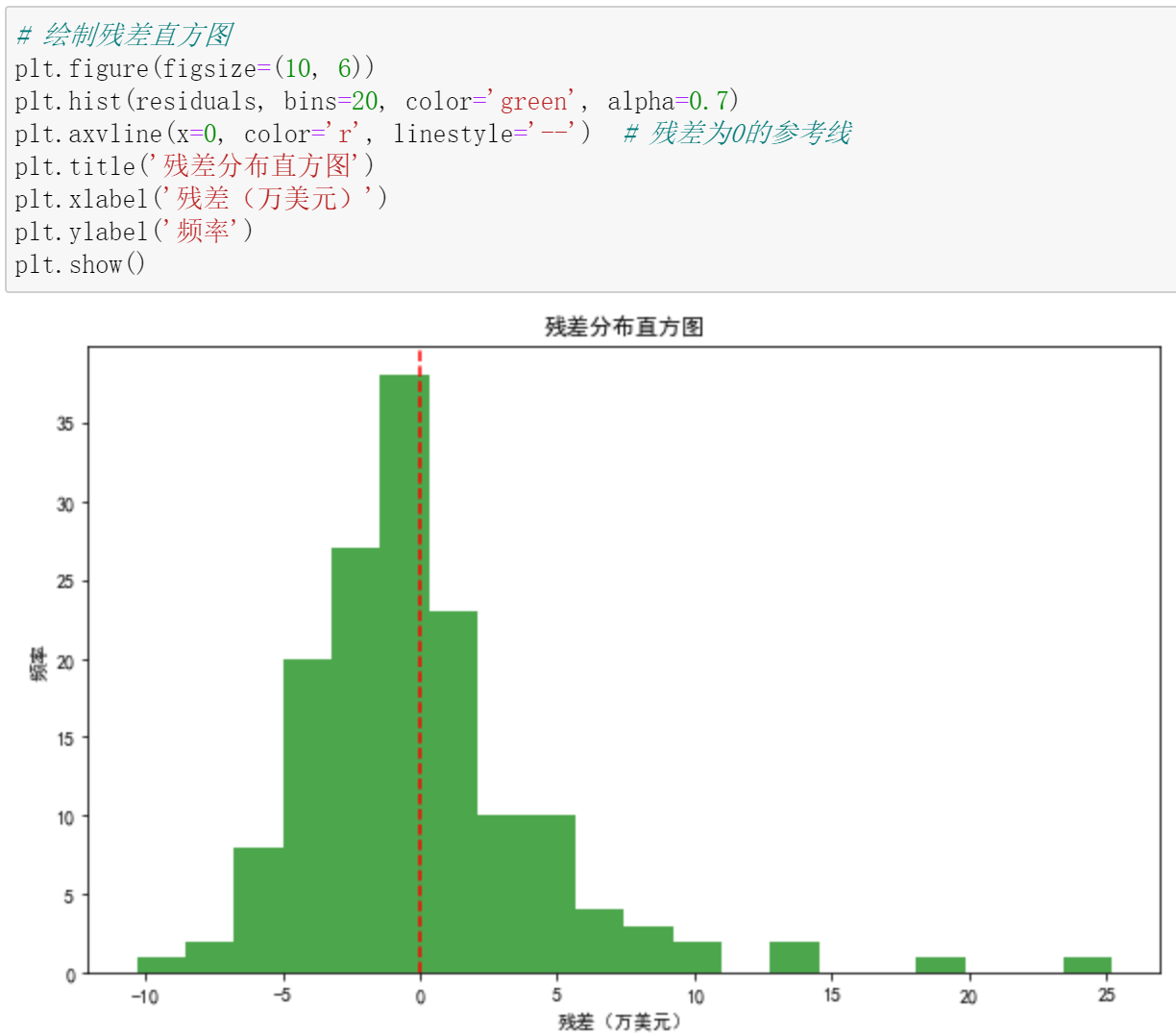
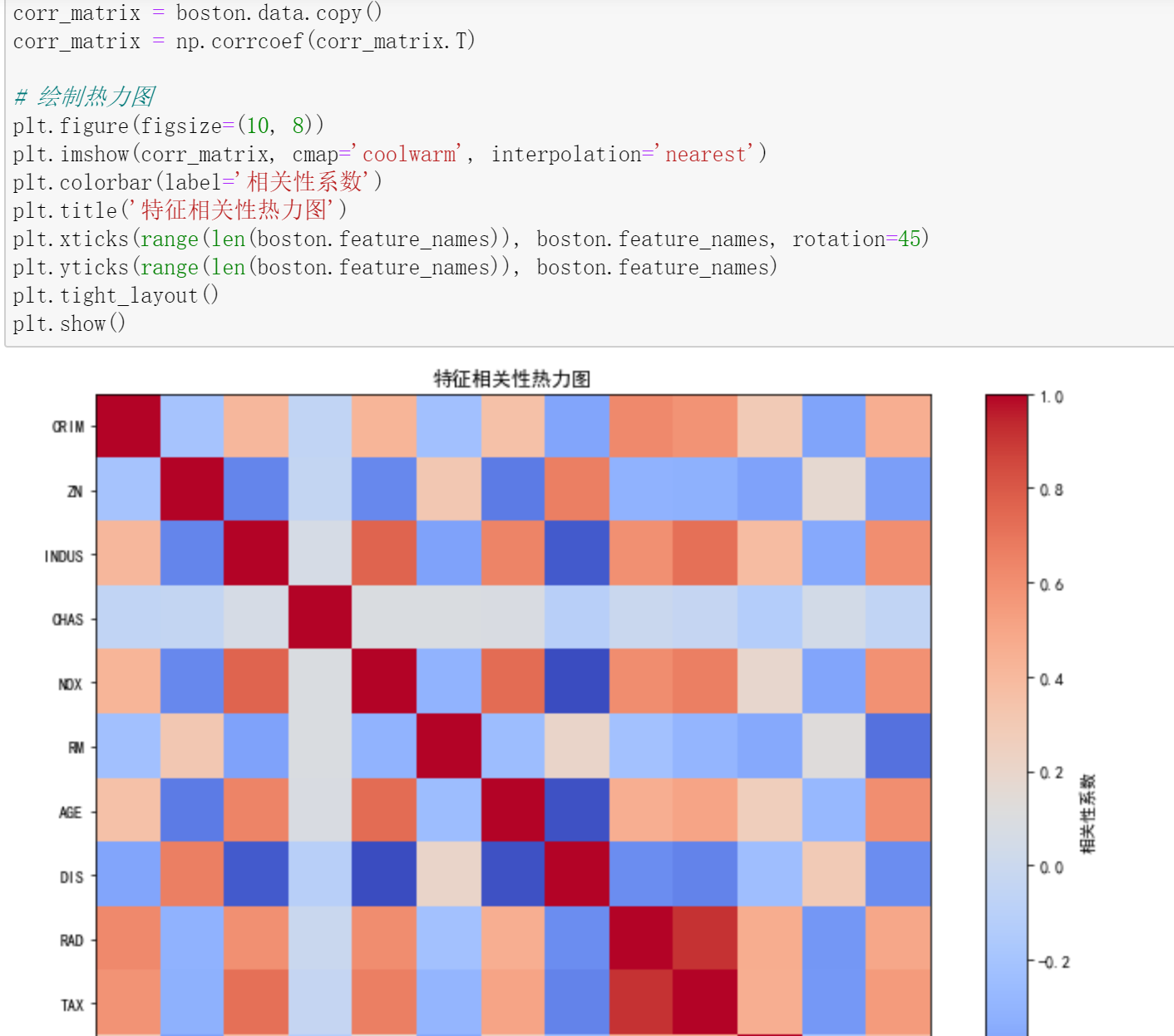
总结
线性回归是机器学习的基础模型,其核心是通过线性关系拟合数据,用最小二乘法求解最优参数,并通过 SSE、MSE、R² 等指标评估效果。无论是简单线性回归还是多元线性回归,都以简洁的原理解决了大量实际问题,是数据分析和预测任务中的重要工具。
