LeetCode100-53最大子数组和
本文基于各个大佬的文章
上点关注下点赞,明天一定更灿烂!

前言
Python基础好像会了又好像没会,所有我直接开始刷leetcode一边抄样例代码一边学习吧。本系列文章用来记录学习中的思考,写给自己看的,也欢迎大家在评论区指导~
您的每一条评论都会让我更有学习的动力。
一、分析题目
进入了新的一部分:数组
这个题目看要求的话思路应该挺简单的吖
二、思路以及代码
暴力选手的思路还是那么的返璞归真,一下就想到,枚举所有可能的子数组,计算每个子数组的和
然后比较得出最大和了,但是时间复杂度肯定会超,不写了不写了。
今天暂时放弃暴力写法 用一下上学期算法课学的分治法吧(其实是我就开学听了这一节课,只会个简单的分治法,动态规划,贪心,回溯什么的都不会)
首先复习一下分治法,法如其名,是采取”分而治之“策略的算法结构,
其核心思路是:
- 分(Divide):将原问题分解为若干个规模较小的子问题
- 治(Conquer):递归求解各个子问题
- 合(Combine):合并子问题的解,得到原问题的解
本题采用分治法的思路:
将数组分成左右两部分
递归求解左右部分的最大子数组和
求解跨越中点的最大子数组和
返回三者中的最大值
步骤1:分解数组
将数组nums[left...right]从中间mid分成左右两部分:
- 左半部分:
nums[left...mid] - 右半部分:
nums[mid+1...right]
步骤2:递归求解子问题
递归计算:
- 左半部分的最大子数组和(
left_sum) - 右半部分的最大子数组和(
right_sum)
步骤3:求解跨越中点的最大子数组和
这是分治法解决该问题的关键步骤,需要找到包含中点的最大子数组:
-
从中间向左扫描,找到以中点为终点的最大子数组和(
left_cross_sum) -
从中间向右扫描,找到以中点为起点的最大子数组和(
right_cross_sum) -
跨越中点的最大子数组和为两者之和(
cross_sum = left_cross_sum + right_cross_sum)
步骤4:合并结果
返回left_sum、right_sum和cross_sum中的最大值
class Solution:def maxSubArray(self, nums: List[int]) -> int:def max_crossing_sum(nums, left, mid, right):# 步骤1: 向左扫描,找到以mid为终点的最大子数组和left_sum = float('-inf') # 初始化为负无穷大current_sum = 0# 从mid向左遍历到leftfor i in range(mid, left - 1, -1):current_sum += nums[i]# 更新最大和if current_sum > left_sum:left_sum = current_sum# 步骤2: 向右扫描,找到以mid+1为起点的最大子数组和right_sum = float('-inf') # 初始化为负无穷大current_sum = 0# 从mid+1向右遍历到rightfor i in range(mid + 1, right + 1):current_sum += nums[i]# 更新最大和if current_sum > right_sum:right_sum = current_sum# 步骤3: 返回左右两部分的和(跨越中点的最大子数组和)return left_sum + right_sumdef max_subarray(nums, left, right):"""递归计算最大子数组和nums: 数组left: 左边界right: 右边界"""# 基本情况:数组只有一个元素if left == right:return nums[left]# 步骤1: 分解 - 找到中点mid = (left + right) // 2# 步骤2: 治 - 递归求解左右两部分left_sum = max_subarray(nums, left, mid) # 左半部分的最大子数组和right_sum = max_subarray(nums, mid + 1, right) # 右半部分的最大子数组和# 步骤3: 合 - 计算跨越中点的最大子数组和cross_sum = max_crossing_sum(nums, left, mid, right)# 返回三者中的最大值return max(left_sum, right_sum, cross_sum)# 初始调用return max_subarray(nums, 0, len(nums) - 1)成功运行,但是速度较慢,因为分治法其实是比较笨的办法
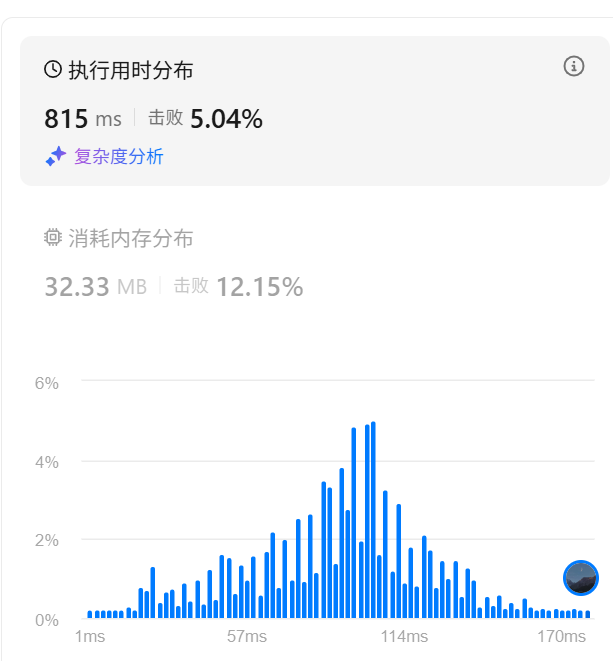
我们看一下官方题解用的办法,53. 最大子数组和 - 力扣(LeetCode)
官方用的动态规划,这个我还不会,明天再学吧。我要去追电视剧了。
三、本题收获
明天一定学,学完再回来编辑。
总结
只会打暴力,基础一团糟,明天再学吧老铁,别真学会了。
