【基础算法】离散化
文章目录
- 一、什么是离散化
- 二、如何实现离散化
- 1. 【模板一】排序 + 去重 + 二分
- (1) 实现思路
- (2) 代码实现
- 2. 【模板二】排序 + 哈希表
- (1) 实现思路
- (2) 代码实现
- 三、OJ 实战
- 1. 火烧赤壁 ⭐⭐
- (1) 解题思路
- (2) 代码实现
- 2. 贴海报 ⭐⭐⭐
- (1) 解题思路
- (2) 代码实现
一、什么是离散化
当题目中数据的值很大,但是数据的总量不是很大时,如果我们需要用数据的值来映射数组的下标时,那么这个数组要开很大,显然是不行的。比如 [99, 9, 9999, 999999] 这个数组只有 4 个数据,我们不能真的开 999999 个空间来做映射。
那么这个时候就可以用离散化的思想先预处理一下所有的数据,使得每一个数据都映射成一个较小的值。之后再用离散化之后的数去处理问题。
怎么映射成为一个较小的值呢?我们可以根据每个数从小到大来编号完成离散化。比如:[99, 9, 9999, 999999] 离散之后就变成 [2, 1, 3, 4] 。
二、如何实现离散化
1. 【模板一】排序 + 去重 + 二分
【题目描述】
给定 n 个数,离散化之后,输出每一个数离散化之后的值。
【示例一】
输入
10 1999999 12 1999999 -48444 568 12 -100 -2845630 100000001 263输出
7 4 7 2 6 4 3 1 8 5
(1) 实现思路
我们可以创建一个离散化数组 disc[],初始时与原数组 a[] 一致。之后我们对离散化数组 disc[] 进行排序和去重操作。去重我们采用算法库中的 unique 函数,并用 pos 记录去重后的离散化数组大小。
之后,对于每一个原数组中的数,我们采用二分查找查询它在离散化数组中的位置并输出其下标即可。
(2) 代码实现
// 排序 + 去重 + 二分
#include<iostream>
#include<algorithm>using namespace std;const int N = 1e5 + 10;int n;
int a[N];int pos; // 去重前/后数组的大小
int disc[N]; // 离散化数组// 二分查找
int find(int x)
{int left = 1, right = pos;while(left < right){int mid = left + (right - left) / 2;if(disc[mid] >= x) right = mid;else left = mid + 1;}return left;
}int main()
{cin >> n;for(int i = 1; i <= n; i++){cin >> a[i];disc[++pos] = a[i];}// 离散化sort(disc + 1, disc + 1 + pos); // 排序pos = unique(disc + 1, disc + 1 + pos) - (disc + 1); // 去重for(int i = 1; i <= n; i++){cout << find(a[i]) << endl;}return 0;
}
2. 【模板二】排序 + 哈希表
(1) 实现思路
在这种策略中,我们依旧先对离散化数组进行排序,之后我们遍历排序后的离散化数组,用一个哈希表来存储 <原始值,离散化之后的值> 这样的键值对。关于这个离散化之后的值,我们可以定义一个变量 cnt,初始为 0,每当遇到一个哈希表中没有的原始值时,我们就把 cnt++,把这个值放入哈希表中并和 cnt 绑定在一起。
(2) 代码实现
// 排序 + 哈希表
#include<iostream>
#include<algorithm>
#include<unordered_map>using namespace std;const int N = 1e5 + 10;int n;
int a[N];int pos;
int disc[N]; // 离散化数组
unordered_map<int, int> id; // <原始值,离散化之后的值>int main()
{cin >> n;for(int i = 1; i <= n; i++){cin >> a[i];disc[++pos] = a[i];}// 离散化sort(disc + 1, disc + 1 + pos); // 排序int cnt = 0; // 用来标记当前元素离散化之后的值for(int i = 1; i <= pos; i++){int x = disc[i];if(id.count(x)) continue; // 相当于去重cnt++;id[x] = cnt;}for(int i = 1; i <= n; i++){cout << id[a[i]] << endl;}return 0;
}
三、OJ 实战
1. 火烧赤壁 ⭐⭐
【题目链接】
P1496 火烧赤壁 - 洛谷
【题目背景】
曹操平定北方以后,公元 208 年,率领大军南下,进攻刘表。他的人马还没有到荆州,刘表已经病死。他的儿子刘琮听到曹军声势浩大,吓破了胆,先派人求降了。
孙权任命周瑜为都督,拨给他三万水军,叫他同刘备协力抵抗曹操。
隆冬的十一月,天气突然回暖,刮起了东南风。
没想到东吴船队离开北岸大约二里距离,前面十条大船突然同时起火。火借风势,风助火威。十条火船,好比十条火龙一样,闯进曹军水寨。那里的船舰,都挤在一起,又躲不开,很快地都烧起来。一眨眼工夫,已经烧成一片火海。
曹操气急败坏的把你找来,要你钻入火海把连环线上着火的船只的长度统计出来!
【题目描述】
给定每个起火部分的起点和终点,请你求出燃烧位置的长度之和。
【输入格式】
第一行一个整数,表示起火的信息条数 nnn。
接下来 nnn 行,每行两个整数 a,ba, ba,b,表示一个着火位置的起点和终点(注意:左闭右开)。
【输出格式】
输出一行一个整数表示答案。
【示例一】
输入
3 -1 1 5 11 2 9输出
11
【说明/提示】
对于全部的测试点,保证 1≤n≤2×1041 \leq n \leq 2 \times 10^41≤n≤2×104,−231≤a<b<231-2^{31} \leq a < b \lt 2^{31}−231≤a<b<231,且答案小于 2312^{31}231。
(1) 解题思路
我们先不看这道题的数据范围,先考虑这道题的整体思路。我们会发现这道题可以采用差分的方式来解决,对于每一个区间,我们都用差分来快速将这段区间的每一个值都统一 +1,操作完之后遍历整个数组,只要当前位置的数 >0,那么就让结果 +1,最终遍历完之后就能拿到总长度。
但是很不幸的是,这道题的区间端点最小可以是 −231-2^{31}−231,最大可以是 2312^{31}231。显然我们的数组是开不了这么大的,但是我们又可以发现总共的区间数量是不多的,最多只有 2×1042 \times10^{4}2×104 个。于是,我们便可以采用离散化来预处理每一个区间,把这个很大的数映射成为一个较小的数,之后我们便可以在离散化的基础上进行差分了。
(2) 代码实现
#include<iostream>
#include<algorithm>using namespace std;const int N = 2e4 + 10;int n;
int l[N], r[N]; // 存储着火的起点和终点int pos; // 记录离散化数组的数据个数
int disc[2 * N]; // 离散化数组
int f[2 * N]; // 差分数组// 二分查找,找原始值对应的离散化后的值
int find(int x)
{int left = 1, right = pos;while(left < right){int mid = left + (right - left) / 2;if(disc[mid] >= x) right = mid;else left = mid + 1;}return left;
}int main()
{cin >> n;for(int i = 1; i <= n; i++){cin >> l[i] >> r[i];disc[++pos] = l[i];disc[++pos] = r[i];}sort(disc + 1, disc + 1 + pos); // 排序pos = unique(disc + 1, disc + 1 + pos) - (disc + 1); // 去重// 在离散化的基础上进行差分for(int i = 1; i <= n; i++){int index_l = find(l[i]);int index_r = find(r[i]);f[index_l]++;f[index_r]--; }// 还原出差分数组的原数组for(int i = 1; i <= pos; i++) f[i] += f[i - 1];int ans = 0;// 在还原后的数组上统计答案for(int i = 1; i <= pos; i++){int j = i;while(j <= pos && f[j] > 0) j++;ans += (disc[j] - disc[i]); // 注意要映射到原来的起点和终点i = j;}cout << ans;return 0;
}
2. 贴海报 ⭐⭐⭐
【题目链接】
[P3740 HAOI2014] 贴海报 - 洛谷
【题目描述】
Bytetown 城市要进行市长竞选,所有的选民可以畅所欲言地对竞选市长的候选人发表言论。为了统一管理,城市委员会为选民准备了一个张贴海报的 electoral 墙。
张贴规则如下:
electoral 墙是一个长度为 NNN 个单位的长方形,每个单位记为一个格子;
所有张贴的海报的高度必须与 electoral 墙的高度一致的;
每张海报以
A B表示,即从第 AAA 个格子到第 BBB 个格子张贴海报;后贴的海报可以覆盖前面已贴的海报或部分海报。
现在请你判断,张贴完所有海报后,在 electoral 墙上还可以看见多少张海报。
【输入格式】
第一行,两个正整数 N,MN,MN,M,分别表示 electoral 墙的长度和海报个数。
接下来 MMM 行,每行两个正整数 Ai,BiA_i,B_iAi,Bi,表示每张海报张贴的位置。
【输出格式】
输出贴完所有海报后,在 electoral 墙上还可以看见的海报数。
【示例一】
输入
100 5 1 4 2 6 8 10 3 4 7 10输出
4
【说明/提示】
约束条件
10≤N≤10000000,1≤M≤1000,1≤Ai≤Bi≤1000000010\le N \le 10000000,1\le M\le 1000,1\le A_i \le B_i \le 1000000010≤N≤10000000,1≤M≤1000,1≤Ai≤Bi≤10000000
所有的数据都是正整数,数据之间有一个空格。
(1) 解题思路
还是一样,先不看数据范围,但考虑整体思路的话,我们可以设置一个变量 cnt,对于每一个海报,把它的下标映射到一个数组中,然后将数组中从左端点到右端点的每一个数都修改为 cnt,之后让 cnt += 1。操作完之后,统计在这个数组中有多少个不同的数字(0 除外)即可。
但是,在这道题中,像上面那样暴力模拟的话时间复杂度会达到 101010^{10}1010,肯定会超时。仔细看数据范围可以发现,区间长度可以很大,但是区间的个数最多只有 100010001000,因此我们需要采用离散化的方式来做优化。也就是对于每一个区间的左右端点,我们都把它们进行离散化映射成为一个较小的数,然后在这个离散化之后的数组的基础上进行上述操作。
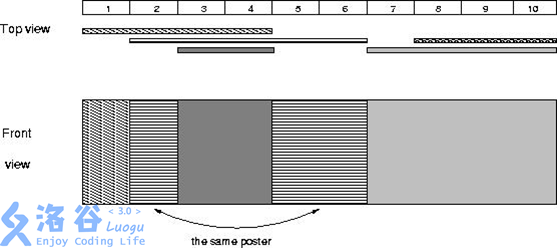
但是!离散化在离散区间问题的时候⼀定要小心!因为我们离散化操作会把区间缩短,从而导致丢失一些点。在涉及区间覆盖问题上,离散化可能会导致结果出错。比如下面这个例子:

为了避免出现上述情况,我们可以在离散化的区间时,不仅考虑这 [x, y] 区间端点 x 和 y 两个值,同时把 x + 1 和 y + 1 也考虑进去。此时单个区间内部就会出现空隙,区间与区间之间也会出现空隙。就可以避免上述情况出现。
(2) 代码实现
#include<iostream>
#include<algorithm>
#include<unordered_map>using namespace std;const int N = 1010;int n, m;
int l[N], r[N]; // 海报的左右区间int pos; // 统计离散化数组的大小
int disc[N * 4]; // 离散化数组
unordered_map<int, int> id; int w[N * 4]; // 海报墙
bool res[N * 4]; // 标记哪些数字已经出现过int main()
{cin >> n >> m;for(int i = 1; i <= m; i++){cin >> l[i] >> r[i];// 把 l 加上的同时把 l + 1 也加上,r 同理disc[++pos] = l[i]; disc[++pos] = l[i] + 1;disc[++pos] = r[i]; disc[++pos] = r[i] + 1; }// 排序 + 哈希表实现离散化sort(disc + 1, disc + 1 + pos);int cnt = 0;for(int i = 1; i <= pos; i++){int x = disc[i];if(id.count(x)) continue;cnt++;id[x] = cnt;}// 对于每一个原始值,找到它对应离散化之后的值,然后在海报墙上标记for(int i = 1; i <= m; i++){int index_l = id[l[i]];int index_r = id[r[i]];for(int j = index_l; j <= index_r; j++){w[j] = i;}}// 利用 res 数组看有多少个不同的数字int ans = 0;for(int i = 1; i <= pos; i++){// 如果当前位置没有海报或者有海报但已经统计过了,那么跳过if(!w[i] || res[w[i]]) continue;ans++;res[w[i]] = true;}cout << ans;return 0;
}