计算机组成原理(10) - 浮点数的表示

浮点数（Floating Point Number）是计算机中表示实数的一种数据类型，用于存储和处理带小数点的数值，例如 3.14、-0.001、2.718 等。它通过科学计数法的形式在有限的存储空间内表示大范围的数值，是编程中处理非整数的基础。

为什么需要浮点数呢，因为定点数有局限性

我们不能无限制的增加数据的长度

1. 从科学技术法理解浮点数

2. IEEE 754 标准定义的浮点数格式

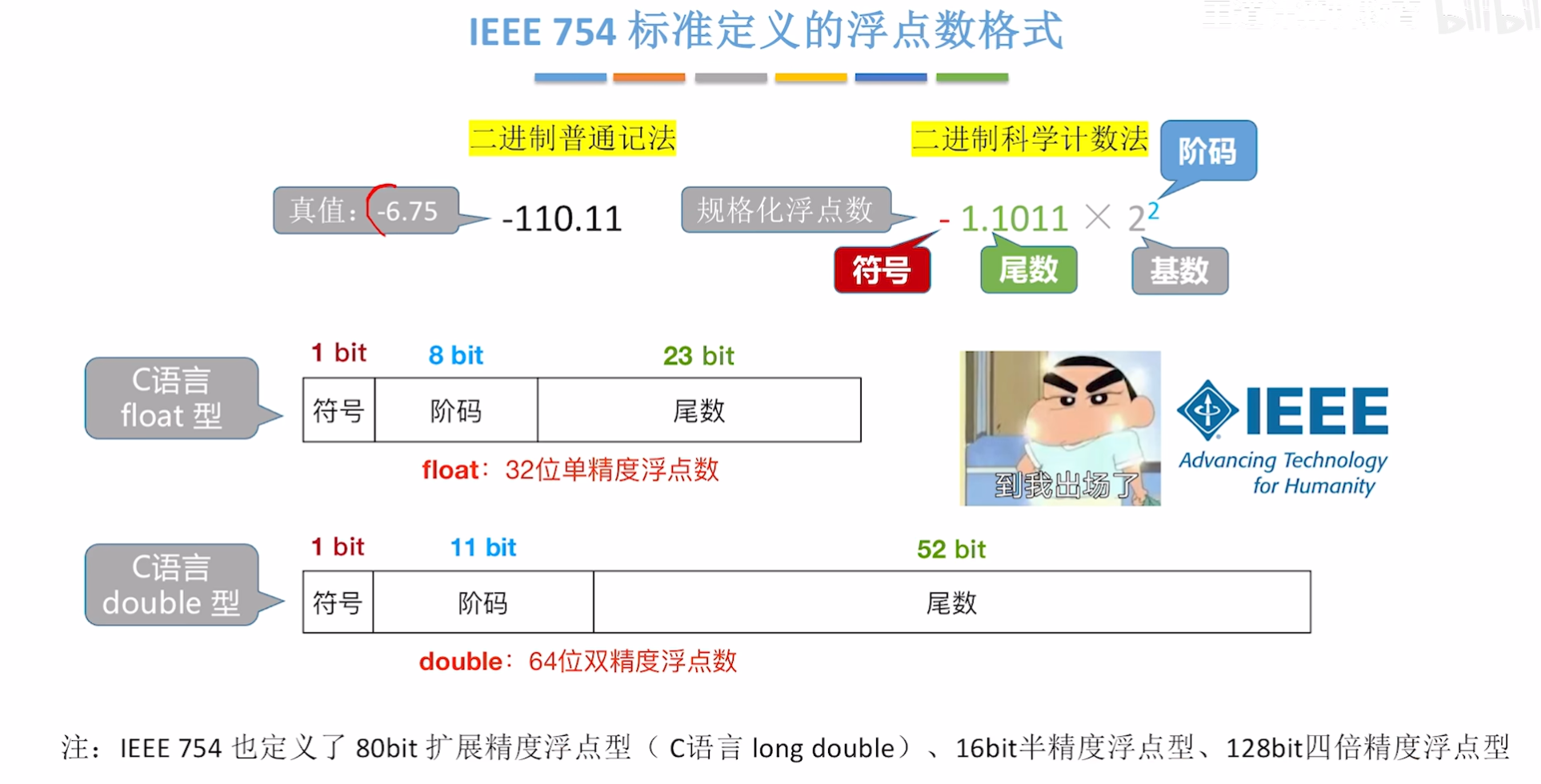
3. float 单精度浮点型的存储

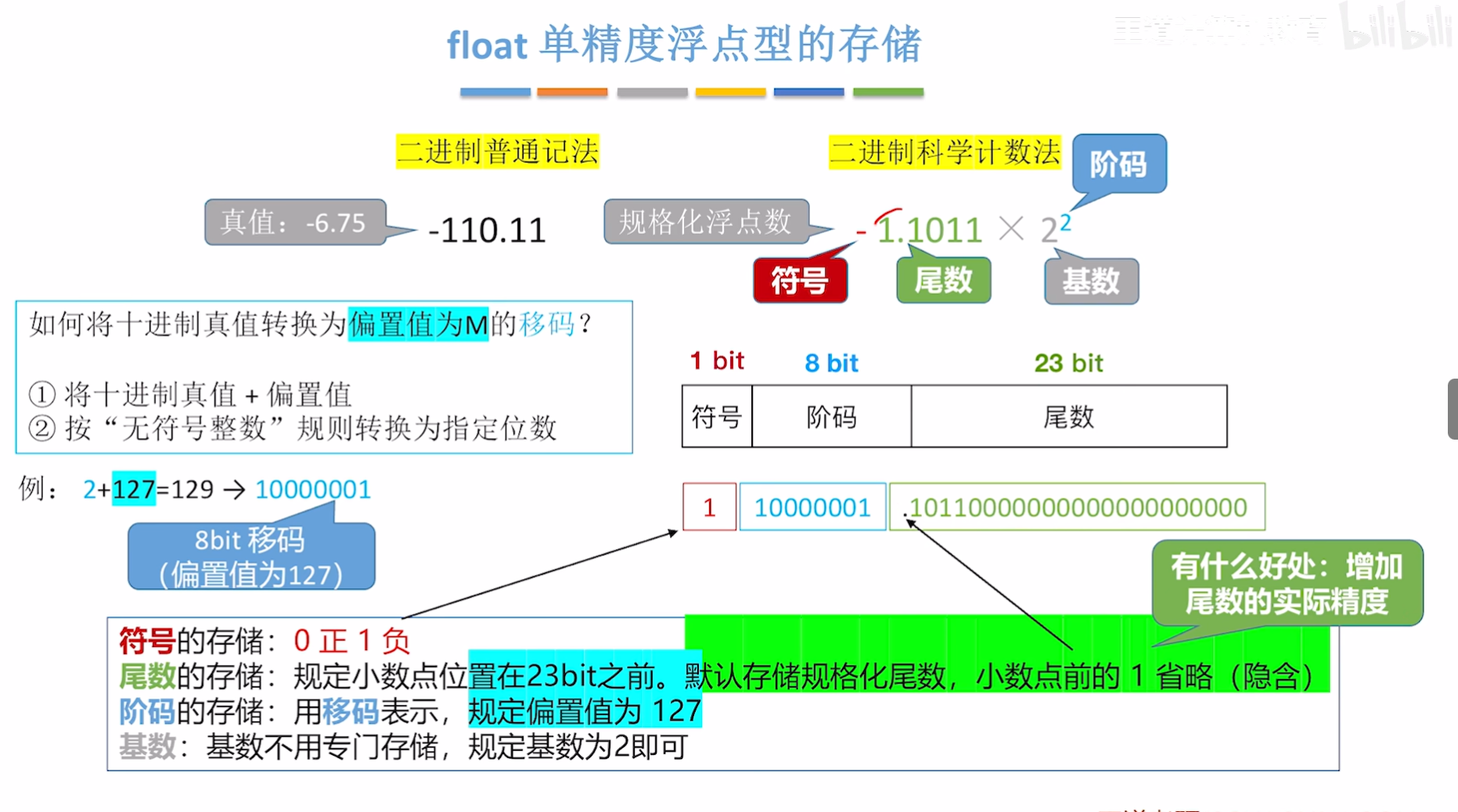
在计算机中，单精度浮点数（float） 遵循 IEEE 754 标准，使用 32 位（4 字节）存储空间表示。这 32 位被划分为三个部分，分别表示符号、指数和尾数，具体结构如下：

存储结构（32 位总长度）

部分	位数	作用
符号位（S）	1 位	表示数值的正负：0 为正，1 为负。
指数位（E）	8 位	表示科学计数法中的指数（需加上偏移量），范围为 0~255。
尾数位（M）	23 位	表示有效数字的小数部分（隐含整数部分为 1，节省 1 位存储空间）。

各部分详解

1. 符号位（S）
   仅用 1 位表示正负：

   • S=0 → 正数
   • S=1 → 负数
2. 指数位 (E) - 使用“移码”表示

指数 E 既可能是正数（放大），也可能是负数（缩小）。为了避免再用一个符号位来表示指数本身，IEEE 754 标准采用了 移码 (Exponent Bias) 表示法。

• 对于单精度浮点数，偏移值 (Bias) 固定为 127。

• 存储值 = 真实指数值 + 127

例子：

• 如果真实指数是 +5，那么存储的指数位就是 5 + 127 = 132 (10000100 in binary)。

• 如果真实指数是 -3，那么存储的指数位就是 -3 + 127 = 124 (01111100 in binary)。

这样，指数 -127 到 +128 的范围就被映射到了 0 到 255 的存储范围。

1. 尾数位（M）
   23 位表示有效数字的小数部分，采用 隐含 1 位整数 的设计（即默认整数部分为 1），因此实际有效数字为：

   有效数字 = 1.M（二进制）
   

   例如，若 M 的二进制为 0110...，则实际有效数字为 1.0110...（二进制）。
   这种设计让 23 位尾数能表示 24 位有效数字（1 位隐含整数 + 23 位小数）。

完整表示公式

单精度浮点数的数值可表示为：

数值 = (-1)^S × (1.M) × 2^(E-127)

其中：

• (-1)^S 决定正负
• (1.M) 是二进制有效数字
• 2^(E-127) 是指数部分

示例：0.5 的存储

1. 0.5 的二进制为 0.1
2. 转换为科学计数法：1.0 × 2^(-1)
3. 各部分解析：
   • 符号位 S=0（正数）
   • 指数 E = 实际指数 + 127 = -1 + 127 = 126 → 二进制 01111110
   • 尾数位 M 是 1.0 的小数部分 0 → 23 位全为 0
4. 32 位完整存储：
   0 01111110 00000000000000000000000

精度与范围

• 精度：23 位尾数 + 1 位隐含整数 → 约 7 位十进制有效数字（2^24 ≈ 1.6×10^7）。
• 数值范围：
  最小正值 ≈ 1.175×10^(-38)（E=1, M=0）
  最大正值 ≈ 3.403×10^(38)（E=254, M 全为 1）

理解单精度浮点数的存储方式，有助于解释其精度限制和运算误差的根源（例如 0.1 无法精确表示）。

4. double 双精度浮点型的存储

双精度浮点数（double） 同样遵循 IEEE 754 标准，使用 64 位（8 字节）存储空间，相比单精度（float）提供更高的精度和更大的数值范围。其存储结构如下：

存储结构（64 位总长度）

部分	位数	作用
符号位（S）	1 位	表示数值的正负：0 为正，1 为负。
指数位（E）	11 位	表示科学计数法中的指数（需加上偏移量1023），范围为 0~2047。
尾数位（M）	52 位	表示有效数字的小数部分（隐含整数部分为 1，节省 1 位存储空间）。

和float都是一样的，只不过尾数变宽，偏移量不同

5.表示范围

浮点数的范围主要由指数位决定。

• 最大正数：出现在

  • 符号位 S = 0 (正数)

  • 指数位 E 为最大值（但非特殊值，见下文）

  • 尾数位 M 全为 1（精度达到最大）
    其值约为 ± 3.4 × 10³⁸

• 最小正规数：这是最接近0的“规整”数字（尾数部分隐含的整数位是1）。

  • 符号位 S = 0

  • 指数位 E 为最小值 1（E_stored=1, E_actual=1-127=-126）

  • 尾数位 M 全为 0
    其值约为 ± 1.2 × 10⁻³⁸

更小的数：非规范数 (Denormalized Numbers) 和 0

当存储的指数 E_stored 为 0 时，情况比较特殊：

• 如果此时尾数 M 也为 0，则表示 数字 ±0（根据符号位S决定是+0还是-0）。

• 如果尾数 M 不为 0，则表示一个非规范数。此时隐含的整数位不再是1，而是0。这允许表示比最小正规数更接近0的数字。

  • 最小正非规范数约为 ± 1.4 × 10⁻⁴⁵

特殊值：无穷大和NaN

当存储的指数 E_stored 全为 1（二进制11111111）时：

• 如果尾数 M 全为 0，则表示 无穷大 (±∞)。例如 1.0 / 0.0 的结果。

• 如果尾数 M 不为 0，则表示 非数 (NaN, Not-a-Number)。例如 0.0 / 0.0 或 √(-1) 的结果。

6. 范围总结表

为了方便理解，以下是单精度和双精度浮点数的范围总结（近似值）：

格式	最大正数	最小正规范数	最小正非规范数
单精度 (float)	±3.4 × 10³⁸	±1.2 × 10⁻³⁸	±1.4 × 10⁻⁴⁵
双精度 (double)	±1.8 × 10³⁰⁸	±2.2 × 10⁻³⁰⁸	±4.9 × 10⁻³²⁴

重要提示：

• 范围 (Range) 指的是能表示的最大和最小数，由指数位决定。

• 精度 (Precision) 指的是有效数字的位数，由尾数位决定。这是两个不同的概念。双精度不仅范围比单精度大得多，精度也高得多。

7.数据的存储和排列

对于一个多字节的数据类型（比如32位的 int，64位的 double），它在内存中要占用多个连续的字节（如4个字节、8个字节）。大小端模式解决的问题是：这个数据的各个字节，在内存中从低地址到高地址的排列顺序是怎样的？

我们以一个32位（4字节）的十六进制数 0x12345678 为例。它在内存中的存储方式有两种：

7.1 大端模式

高位字节存储在低地址处。

“端”就是“结尾”，大端就是指数据的最高有效字节（Most Significant Byte, MSB，也就是大端）存放在内存的最低地址。

• 记忆技巧：大端模式就像我们书写一个数字 1234，总是从高位（千位“1”）开始写，写到低位（个位“4”）。内存地址的增长方向就像我们的书写顺序。

内存低地址	--->	内存高地址
12	34	56	78
(最高有效字节 MSB)			(最低有效字节 LSB)

采用大端模式的系统：某些早期的处理器（如Motorola 68000）、网络协议（TCP/IP协议族规定网络字节序为大端模式）、Java虚拟机等。

7.2 小端模式

小端模式：低位字节存储在低地址处。

小端就是指数据的最低有效字节（Least Significant Byte, LSB，也就是小端）存放在内存的最低地址。

• 记忆技巧：小端模式更符合计算机的计算习惯，从低位开始处理会更方便。

内存低地址	--->	内存高地址
78	56	34	12
(最低有效字节 LSB)			(最高有效字节 MSB)

采用小端模式的系统：目前绝大多数x86、x86-64架构的个人电脑（Intel、AMD CPU）和ARM处理器。

7.3 边界对齐

边界对齐，也称为内存对齐。

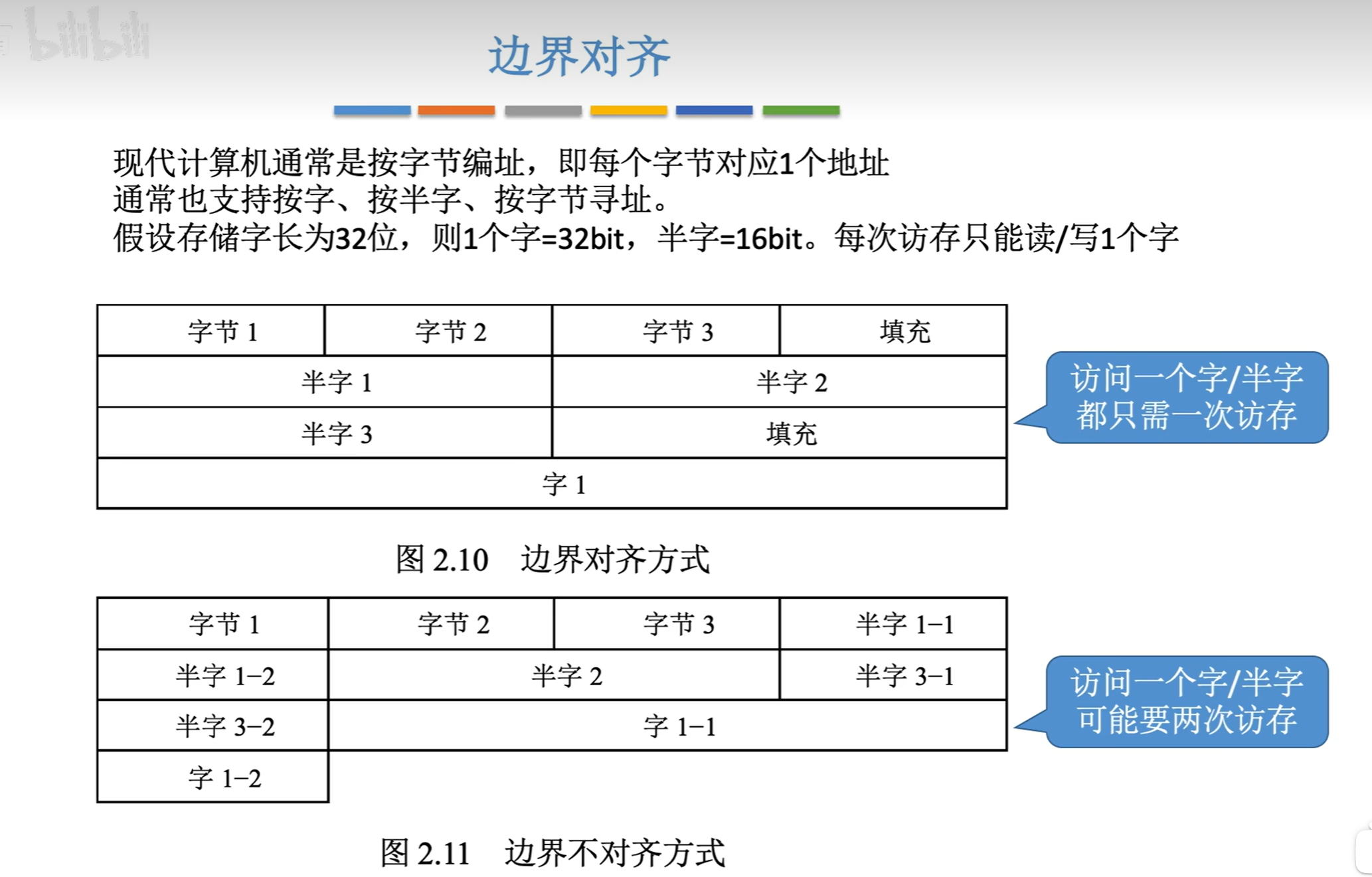
1. 核心思想：用空间换时间和稳定性

主要原因在于硬件。CPU从内存中读写数据时，并非以字节为单位，而是以字（word）为单位。例如，一个32位CPU的字长是4字节，它每次会从4的整数倍地址开始，一次性读取4个字节。

场景分析：读取一个4字节的 int 变量

1. 情况一：数据已对齐（地址为0x0004）

   • CPU发出一次读请求，从地址0x0004开始读取4个字节（0x0004-0x0007）。

   • 一次操作即可完成，效率最高。

2. 情况二：数据未对齐（地址为0x0003）

   • 这个int占用了0x0003-0x0006这4个字节，它跨越了两个CPU字（Word A: 0x0000-0x0003, Word B: 0x0004-0x0007）。

   • CPU必须执行两次内存访问：

     • 第一次读取Word A（0x0000-0x0003），然后取出0x0003地址的部分。

     • 第二次读取Word B（0x0004-0x0007），然后取出0x0004-0x0006地址的部分。

     • 最后将这两部分数据拼接起来，才能得到完整的int值。

   • 后果：

     • 性能损失：访问次数翻倍，还需要额外的移位和拼接操作。

     • 平台依赖性：在某些严格的硬件架构（如许多RISC处理器：SPARC, ARM的老版本）上，未对齐的内存访问会导致硬件异常/总线错误，程序直接崩溃。x86架构虽然支持未对齐访问，但仍有巨大的性能惩罚。

     • 原子性：对齐访问的读/写操作可能是原子的，而未对齐的访问肯定不是原子的。

3. 对齐规则（以典型64位系统为例）

编译器会自动处理对齐问题，但了解规则对优化内存和理解结构体大小至关重要。

• 基本对齐原则：变量的起始地址必须是其自身大小与平台有效对齐值中较小者的整数倍。

  • char (1字节)：可放在任何地址（1的倍数）。

  • short (2字节)：地址必须是2的倍数。

  • int / float (4字节)：地址必须是4的倍数。

  • double / long / 指针 (8字节)：地址必须是8的倍数。

结构体的对齐规则（非常重要！）

结构体的对齐要复杂一些，遵循两个规则：

1. 结构体起始地址：必须是其最宽成员大小的整数倍。

2. 每个成员的位置：必须放在其自身对齐要求的整数倍地址上。编译器会在成员之间自动插入填充字节来满足此要求。

3. 结构体总大小：必须是其最宽成员大小的整数倍（如果不是，编译器会在末尾填充字节）。