《CF1245D Shichikuji and Power Grid》
题目描述
Shichikuji 是南黑蜗牛寺的新任驻守神明。她的第一项工作如下:
在 X 县有 n 个新城市。城市编号从 1 到 n。第 i 个城市位于距离神社北方 xi 千米、东面 yi 千米的位置。可能存在 i=j 但 (xi,yi)=(xj,yj) 的情况。
Shichikuji 必须为每个城市供电,可以通过在该城市建造发电站,或者将该城市与已经有电的城市连接来实现。也就是说,如果一个城市自身有发电站,或者通过直接连接或一系列连接与有电的城市相连,则该城市就有电。
- 在第 i 个城市建造发电站的费用为 ci 日元;
- 将第 i 个城市与第 j 个城市连接的费用为每千米 (ki+kj) 日元。电线只能沿着正北、正南、正东、正西方向铺设,电线可以相互交叉。每根电线的两个端点都必须在某个城市。如果第 i 个城市与第 j 个城市连接,则电线会沿任意一条最短路径铺设。因此,连接第 i 个城市与第 j 个城市所需电线的长度为 ∣xi−xj∣+∣yi−yj∣ 千米。
Shichikuji 希望以尽可能少的钱完成这项工作,因为在她看来,世界上除了钱什么都没有。然而,她小学五年级就去世了,所以她还不够聪明。因此,这位新任驻守神明向你寻求帮助。
你需要为 Shichikuji 提供以下信息:为所有城市供电所需的最小日元数、在哪些城市建造发电站,以及需要建立哪些连接。
如果存在多种选择城市和连接方式使得总花费最小,则输出任意一种即可。
输入格式
输入的第一行包含一个整数 n(1≤n≤2000),表示城市的数量。
接下来 n 行,每行包含两个用空格分隔的整数 xi(1≤xi≤106)和 yi(1≤yi≤106),表示第 i 个城市的坐标。
下一行包含 n 个用空格分隔的整数 c1,c2,…,cn(1≤ci≤109),表示在第 i 个城市建造发电站的费用。
最后一行包含 n 个用空格分隔的整数 k1,k2,…,kn(1≤ki≤109)。
输出格式
第一行输出一个整数,表示为所有城市供电所需的最小日元数。
第二行输出一个整数 v,表示需要建造发电站的城市数量。
第三行输出 v 个用空格分隔的整数,表示建造发电站的城市编号。每个编号应在 1 到 n 之间,且互不相同。编号顺序任意。
接下来一行输出一个整数 e,表示需要建立的连接数量。
最后输出 e 行,每行包含两个整数 a 和 b(1≤a,b≤n,a=b),表示需要在城市 a 和城市 b 之间建立连接。每对无序城市对最多出现一次(即对于每个 (a,b),不应有重复的 (a,b) 或 (b,a))。输出顺序任意。
如果存在多种选择城市和连接方式使得总花费最小,则输出任意一种即可。
显示翻译
题意翻译
输入输出样例
输入 #1复制
3 2 3 1 1 3 2 3 2 3 3 2 3
输出 #1复制
8 3 1 2 3 0
输入 #2复制
3 2 1 1 2 3 3 23 2 23 3 2 3
输出 #2复制
27 1 2 2 1 2 2 3
说明/提示
对于样例给出的答案,可参考下图(绿色为有发电站的城市,蓝色为其他城市,红色为电线):
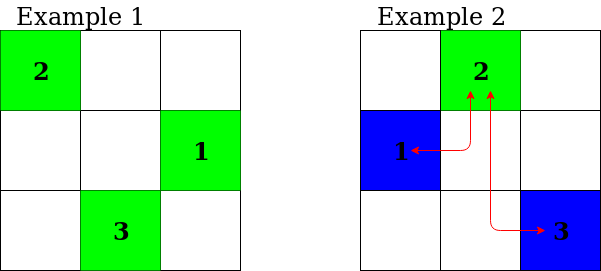
对于第一个样例,在所有城市建造发电站的总费用为 3+2+3=8。可以证明,没有任何方案的花费低于 8 日元。
对于第二个样例,在第 2 号城市建造发电站的费用为 2。连接城市 1 和城市 2 的费用为 2⋅(3+2)=10。连接城市 2 和城市 3 的费用为 3⋅(2+3)=15。因此总费用为 2+10+15=27。可以证明,没有任何方案的花费低于 27 日元。
由 ChatGPT 4.1 翻译
代码实现:
#include <bits/stdc++.h>
using namespace std;
const int MAX_NODE = 2005; // 最大节点数量
// 快速输入结构体
struct FastInput {
template <typename Type>
FastInput & operator >> (register Type & value) {
register int sign = 1;
value = 0;
register char ch = getchar();
// 处理符号
for (; !isdigit(ch); ch = getchar()) {
if (ch == '-') sign = -sign;
}
// 处理数字
for (; isdigit(ch); ch = getchar()) {
value = (value << 1) + (value << 3) + (ch - '0');
}
value *= sign;
return *this;
}
} input;
int totalNodes; // 总节点数量
int powerStationCount; // 直接建立电源的节点个数
long long costFactor[MAX_NODE];// 每个节点的代价因子K
long long xCoord[MAX_NODE]; // 节点的X坐标
long long yCoord[MAX_NODE]; // 节点的Y坐标
long long prevNode[MAX_NODE]; // 记录上一次更新该节点的节点,用于构建边
long long totalCost; // 最后的总代价
long long minDist[MAX_NODE]; // 当前树到各个非树节点的最小代价
bool inTree[MAX_NODE]; // 记录节点是否已加入树中
int main() {
input >> totalNodes;
// 读取节点坐标
for (register int i = 1; i <= totalNodes; i++) {
input >> xCoord[i] >> yCoord[i];
}
// 读取直接建立电站的代价,初始化最小距离数组
for (register int i = 1; i <= totalNodes; i++) {
input >> minDist[i];
}
// 读取代价因子,初始化前置节点为0(表示直接连接电源)
for (register int i = 1; i <= totalNodes; i++) {
input >> costFactor[i];
prevNode[i] = 0;
}
// Prim算法构建最小生成树
for (register int step = 1; step <= totalNodes; step++) {
// 寻找未加入树且距离最小的节点
register long long minCost = 2147483640;
register int selectedNode;
for (register int i = 1; i <= totalNodes; i++) {
if (!inTree[i] && minDist[i] < minCost) {
minCost = minDist[i];
selectedNode = i;
}
}
// 将选中的节点加入树中
inTree[selectedNode] = true;
totalCost += minCost;
// 如果前置节点是0,说明这是一个新的电站
if (prevNode[selectedNode] == 0) {
powerStationCount++;
}
// 更新其他节点到树的最小距离
for (register int i = 1; i <= totalNodes; i++) {
if (!inTree[i]) {
// 计算连接到选中节点的代价
long long connectionCost = (costFactor[i] + costFactor[selectedNode]) *
(abs(xCoord[selectedNode] - xCoord[i]) +
abs(yCoord[selectedNode] - yCoord[i]));
// 如果新的连接代价更小,则更新
if (minDist[i] > connectionCost) {
minDist[i] = connectionCost;
prevNode[i] = selectedNode;
}
}
}
}
// 输出结果
printf("%lld\n%d\n", totalCost, powerStationCount);
// 输出建立电站的节点
for (register int i = 1; i <= totalNodes; i++) {
if (prevNode[i] == 0) {
printf("%d ", i);
}
}
printf("\n");
// 输出边的数量和具体边
printf("%d\n", totalNodes - powerStationCount);
for (register int i = 1; i <= totalNodes; i++) {
if (prevNode[i] != 0) {
printf("%lld %d\n", prevNode[i], i);
}
}
return 0;
}
