当前位置：首页 > news >正文

【动手学深度学习】6.2. 图像卷积

news 2025/8/22 15:27:20

6.2. 图像卷积

卷积神经网络的设计是用于探索图像数据，本节我们将以图像为例。

1）互相关运算

严格说，卷积层是个错误叫法，因为它所表达的运算其实是互相关运算（cross-correlation），而不是卷积运算。根据前面描述，在卷积层中，输入张量和核张量通过互相关运算产生输出张量。

首先，暂时忽略通道（第三维），看看如何处理二维图像数据和隐藏表示。在下图中，输入3x3的二维张量，卷积核是2x2的，而卷积核窗口（或卷积窗口）的形状由卷积核决定，即2x2。

图6.2.1 二维互相关运算。
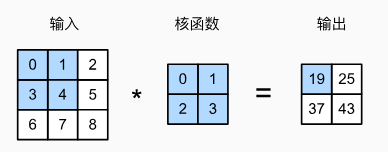
在这里插入图片描述

图中，阴影部分是第一个元素：0 * 0 + 1 * 1 + 3 * 2 + 4 * 3 = 19

在二维互相关运算中，卷积窗口从输入张量的左上角开始，从左到右、从上到下滑动。当卷积窗口滑动到新一个位置时，包含在该窗口中的部分张量与卷积核张量进行按元素相乘，得到的张量再求和得到一个单一的标量值，由此我们得出了这一位置的输出张量值。在如上例子中，输出张量的四个元素由二维互相关运算得到，这个输出高度为2、宽度为2，如下所示：

0 * 0 + 1 * 1 + 3 * 2 + 4 * 3 = 19
1 * 0 + 2 * 1 + 4 * 2 + 5 * 3 = 25
3 * 0 + 4 * 1 + 6 * 2 + 7 * 3 = 37
4 * 0 + 5 * 1 + 7 * 2 + 8 * 3 = 43

注意，输出大小略小于输入大小。

卷积后输出变小，是因为卷积核只能在图像内部完整地滑动，边缘部分无法处理，所以输出尺寸会减小。所以，输出大小等于输入大小 $nh×nwn_h \times n_w$ 减去卷积核大小 $kh×kwk_h \times k_w$ ，即 (输入大小 - 卷积核大小 + 1)：

$(nh−kh+1)×(nw−kw+1).(6.2.2)(n_h - k_h + 1) \times (n_w - k_w + 1). \tag{6.2.2}$

这是因为我们需要足够的空间在图像上“移动”卷积核。

稍后，我们将看到如何通过在图像边界周围填充零来保证有足够的空间移动卷积核，从而保持输出大小不变。接下来，我们在 corr2d 函数中实现如上过程，该函数接受输入张量 $x$ 和卷积核张量 $k$ ，并返回输出张量 $y$ 。

import torch
from torch import nn
from d2l import torch as d2ldef corr2d(X, K):  #@save"""计算二维互相关运算"""h, w = K.shapeY = torch.zeros((X.shape[0] - h + 1, X.shape[1] - w + 1))for i in range(Y.shape[0]):for j in range(Y.shape[1]):Y[i, j] = (X[i:i + h, j:j + w] * K).sum()return Y

验证上述二维互相关运算的输出：

X = torch.tensor([[0.0, 1.0, 2.0], [3.0, 4.0, 5.0], [6.0, 7.0, 8.0]])
K = torch.tensor([[0.0, 1.0], [2.0, 3.0]])
corr2d(X, K)# 输出：
tensor([[19., 25.],[37., 43.]])

卷积层对输入和卷积核权重进行互相关运算，并在添加标量偏置之后产生输出。所以，卷积层中的两个被训练的参数是卷积核权重和标量偏置。

2）卷积层

基于上面定义的corr2d函数实现二维卷积层。在__init__构造函数中，将weight和bias声明为两个模型参数。前向传播函数调用corr2d函数并添加偏置。

class Conv2D(nn.Module):def __init__(self, kernel_size):super().__init__()self.weight = nn.Parameter(torch.rand(kernel_size))self.bias = nn.Parameter(torch.zeros(1))def forward(self, x):return corr2d(x, self.weight) + self.bias

高度和宽度分别为 h 和 w 的卷积核可以被称为 h × w 卷积或 h × w 卷积核。

将带有 h × w 卷积核的卷积层称为 h × w 卷积层。

3）图像中目标的边缘检测

如下，是卷积层的一个简单应用：通过找到像素变化的位置，来检测图像中不同颜色的边缘。

首先，我们构造一个 6x8 像素的黑白图像。中间四列为黑色（0），其余像素为白色（1）。

X = torch.ones((6, 8))
X[:, 2:6] = 0
X# 输出：
tensor([[1., 1., 0., 0., 0., 0., 1., 1.],[1., 1., 0., 0., 0., 0., 1., 1.],[1., 1., 0., 0., 0., 0., 1., 1.],[1., 1., 0., 0., 0., 0., 1., 1.],[1., 1., 0., 0., 0., 0., 1., 1.],[1., 1., 0., 0., 0., 0., 1., 1.]])

接下来，构造一个1x2 的卷积核 K。当进行互相关运算时，如果水平相邻的两元素相同，则输出为零，否则输出为非零。

K = torch.tensor([[1.0, -1.0]])

现在，我们对参数 X（输入）和 K（卷积核）执行互相关运算。如下所示，输出 Y 中的 1 代表从白色到黑色的边缘，-1 代表从黑色到白色的边缘，其他情况的输出为 0。

Y = corr2d(X, K)
Y# 输出：
tensor([[ 0.,  1.,  0.,  0.,  0., -1.,  0.],[ 0.,  1.,  0.,  0.,  0., -1.,  0.],[ 0.,  1.,  0.,  0.,  0., -1.,  0.],[ 0.,  1.,  0.,  0.,  0., -1.,  0.],[ 0.,  1.,  0.,  0.,  0., -1.,  0.],[ 0.,  1.,  0.,  0.,  0., -1.,  0.]])

现在我们将输入的二维图像转置，再进行如上的互相关运算。其输出如下，之前检测到的垂直边缘消失了。不出所料，这个卷积核 K 只可以检测垂直边缘，无法检测水平边缘。

corr2d(X.t(), K)# 输出：
tensor([[0., 0., 0., 0., 0.],[0., 0., 0., 0., 0.],[0., 0., 0., 0., 0.],[0., 0., 0., 0., 0.],[0., 0., 0., 0., 0.],[0., 0., 0., 0., 0.],[0., 0., 0., 0., 0.]])

4）学习卷积核

通过仅查看“输入-输出”对，来学习由X**生成Y的卷积核：**监督学习 + 梯度下降

初始化卷积核为随机值
前向传播：使用卷积核对输入 X 做卷积 → 得到预测输出 Y_hat
计算损失（误差）：计算预测值和真实值之间的差距（均方误差）
反向传播求梯度：自动计算损失对卷积核权重的梯度（告诉我们：“这个卷积核该往哪个方向调才能更接近正确答案？”）
更新卷积核：用梯度下降法更新卷积核参数，逐步减小误差

重复迭代以上过程。卷积核会越来越优。

为了简单起见，我们在此使用内置的二维卷积层，并忽略偏置。

# 构造一个二维卷积层，它具有1个输出通道和形状为(1, 2)的卷积核
conv2d = nn.Conv2d(1, 1, kernel_size=(1, 2), bias=False)# 输入和输出都reshape成四维格式 (批量大小, 通道, 高度, 宽度)
X = X.reshape((1, 1, 6, 8))
Y = Y.reshape((1, 1, 6, 7))
lr = 3e-2  # 学习率for i in range(10):Y_hat = conv2d(X)  # 前向传播：得到预测输出l = (Y_hat - Y) ** 2  # 计算平方误差（损失）conv2d.zero_grad()  # 清空之前的梯度l.sum().backward()  # 反向传播，计算梯度：自动计算损失对模型中所有可训练参数的梯度，并将这些梯度保存在 .grad 属性中# 更新卷积核权重conv2d.weight.data[:] -= lr * conv2d.weight.gradif (i + 1) % 2 == 0:print(f'epoch {i+1}, loss {l.sum():.3f}')

输出：

epoch 2, loss 6.422
epoch 4, loss 1.225
epoch 6, loss 0.266
epoch 8, loss 0.070
epoch 10, loss 0.022

10次迭代后，误差降到足够低。现在来看看所学的卷积核的权重张量。

conv2d.weight.data.reshape((1, 2))# 输出
tensor([[ 1.0010, -0.9739]])

学习到的卷积核权重，非常接近之前定义的卷积核K。

5）互相关与卷积

卷积运算可通过翻转卷积核后执行互相关运算得到。但在实际中，由于卷积核由数据学习而来，互相关与卷积对输出结果无实质影响。因此，深度学习中常将互相关称为“卷积”。为保持术语一致，本书也采用此惯例，并将卷积核中的参数称为“元素”。

问题一：为什么卷积运算可通过翻转卷积核后执行互相关运算得到？

下面对比下卷积（Convolution）和互相关（Cross-correlation）的公式，并说明它们的区别。

概念	数学定义	深度学习中的做法
互相关	不翻转，直接滑动计算	被称作“卷积”
卷积	先翻转核，再滑动计算	实际不翻转，直接算

a.互相关（Cross-correlation）：

互相关运算，如公式（6.1.3）：

$[H]i,j=u+∑a=−ΔΔ∑b=−ΔΔ[V]a,b[X]i+a,j+b.(同6.1.3)[\mathbf{H}]_{i,j} = u + \sum_{a=-\Delta}^{\Delta} \sum_{b=-\Delta}^{\Delta} [\mathbf{V}]_{a,b} [\mathbf{X}]_{i+a,j+b}. \tag{同6.1.3}$

操作：卷积核 $V\mathbf{V}$ 直接在输入 $X\mathbf{X}$ 上滑动，对应位置相乘求和。
没有翻转核。
深度学习框架（如 PyTorch、TensorFlow）中实际实现的就是这个。

b.卷积（Convolution）：

卷积运算，如公式（6.1.6）：

$\sum_a \sum_b f(a, b) \cdot g(i - a, j - b)$

或等价地：

$(V∗X)i,j=∑a∑bVa,b⋅Xi−a,j−b(\mathbf{V} * \mathbf{X})_{i,j} = \sum_a \sum_b \mathbf{V}_{a,b} \cdot \mathbf{X}_{i-a,j-b}$

关键区别：相当于先把卷积核翻转 $180∘180^\circ$ （上下 + 左右翻），再与输入做互相关。
数学意义上的“卷积”要求这种“减号”形式。

问题二：为什么互相关与卷积对输出结果无实质影响？

虽然数学上卷积要翻转核，互相关不翻转，但在深度学习中，卷积核是通过训练数据自动学习出来的，而不是人为设定的。

关键点：

如用互相关运算：网络会学到一个特定的 K
如用严格卷积运算：需将核翻转后再用，所以如果想得到同样的输出，应该用翻转后的核 K′=flip(K)
但！由于卷积核是可学习的：如果强制执行“严格卷积”，那么网络会自动学习出一个“翻转过的核”来补偿这个差异。换句话说，它会学会等效于原来互相关所用的核。

最后，输出结果是一样的输出。

6）特征映射和感受野

图6.2.1 中输出的卷积层有时被称为特征映射（feature map），因为它可以被视为一个输入映射到下一层的空间维度的转换器。卷积神经网络中，对于某一层的任意元素 x，其感受野（receptive field）是指在前向传播期间可能影响 x 计算的所有元素（来自所有先前层）。

注意，感受野可能大于输入的实际大小。用图6.2.1 为例来解释感受野：给定 2 x 2 卷积核，阴影输出元素值19的感受野是输入阴影部分的四个元素。假设之前输出为 Y，其大小为 2 x 2，现在我们在其后附加一个卷积层，该卷积层以 Y 为输入，输出单个元素 z。在这种情况下，Y 上的 z 的感受野包括 Y 的所有四个元素，而输入的感受野包括最初所有九个输入元素。

随着卷积神经网络的层数加深，每一个特征图上的元素“看到”的输入区域（即感受野）会变大。因此，深层的神经元可以捕捉更大范围的上下文信息。