当前位置： 首页 > news >正文

机器学习7

news 2025/8/22 6:51:07

十五、线性回归算法

  • 需要掌握的知识点【重点】：

    • 损失函数

    • 梯度下降

    • 学习率

  • 回顾一下：在以前学习数学的时候，我们就学习过线性回归，只是说，之前学习的线性回归中，一定能够通过方程找到一个确定的答案，比如 y=bx+a

  • 对于机器学习而言，如果数据的分布，没有实际上的规律，也就是说，他可能是分布在某一条线的周围，那么我们就需要去寻找一条直线，把样本数据的特征值带进去计算出来的结果【预测的结果】尽可能的接近样本数据的真实值，即 y预测要接近于y真实

  • 我们的线性回归算法，就是去寻找这一条直线，直线中就存在很多的未知数，这些未知数就是某一个特征的【权重参数】，即某个特征对于结果的一个贡献度，最后在加上一个偏置项【常数】

    • 线性：理解为就是一条直线

  • 在机器学习中，线性回归算法，主要就是去寻找一条内容尽可能拟合所有数据的一个方程，这个方程需要满足每一个预测的结果和真实的结果要贴近，即所有的预测结果-真是结果的值需要最小化

  • 我们把预测结果-真是结果这个内容最小化，定义为损失函数，常见的损失函数MSE（均方误差损失），他的公式


MSE=\frac{1}{n}\sum_{i=1}^n(y_i-\hat{y_i})^2

  • 我们就通过最小化损失函数，从而算出线性回归中的参数信息

  • 如何让损失函数最小化？有一些策略

  • 为了最小化损失函数，我们采取对于不同的变量求偏导，令偏导数等于0，寻找极值

  • 损失不是针对于某一个样本而言的，而是考虑的全部样本，一个样本的真实值于预测值之间的差值，我们称为残差

  • 目前学习一个损失函数，均方误差损失，后面的分类问题，需要使用交叉熵损失函数来实现，分类问题和回归问题，使用的损失函数是有区别的，但是都是需要最小化的

  • 线性回归方法思路：

    • 先随机给一个权重参数，然后通过这个权重参数去预测数据集中的值，然后用这个预测值和真实值之间进行比较（使用均方误差），我们就去优化均方误差，让均方误差最小化，等同于得到了最好的权重参数

  • 损失函数可以不可以基于预测的结果和真实的结果计算出来一个值？可以计算，算出来的这个值就是均方误差损失值，那么我们就要不断的去优化权重的取值，从而让MSE计算出来的值变小【损失越小，证明我们预测结果越准确】

  • 重要概念：

    • 机器学习的线性回归：就是寻找一条最佳的直线，能够更多的拟合数据

    • 残差：真实值与预测值之间的一个差值，yTrue-yFalse

    • RSS：残差平方和，就是所有的参数的平方在求和

    • 损失函数：损失函数就是用来衡量模型预测结果与真是结果之间的一个总体样本上的差值情况，在这里我们先选择了 MSE 损失函数

    • 均方误差MSE：1/n RSS

    • 因为我们想要保证模型预测的结果更加正确【接近真实值】，那么我们在训练模型的时候，就应该考虑模型训练的数据集上的预测结果和实际的结果之间的差值最小化，即我们就通过这种思想，来代替了传统解方程的思想。想要最小化损失函数，其实就是根据函数的结果去修正初始化的参数信息

  • 欧几里得范数

    • 对于一个向量：

    \mathbf{x} = \begin{bmatrix} x_1\\ x_2\\ .\\ .\\ .\\ x_n\\ \end{bmatrix}

    • 它的范数计算公式如下


    \begin{aligned} 欧几里得范数:||X||&=\sqrt{x_1^2+x_2^2+...+x_n^2}\\ 平方范数:||X||^2&=x_1^2+x_2^2+...+x_n^2\\ &=\sum_{i=1}^{n}x_i^2\\ \end{aligned}

    • 向量的欧几里得范数（2-范数）的平方在矩阵代数中的标准表达形式


    ||X||^2=X^TX

  • 多元线性回归 RSS 公式结合上述内容，可用以下方式表达


RSS = ||WX-y||^2 = (WX-y)^T(WX-y)

  • 多元线性回归损失函数公式


loss = \frac{1}{2}||WX-y||^2 =\frac{1}{2}(WX-y)^T(WX-y)

  • 多元线性回归损失函数求导需要使用到的公式

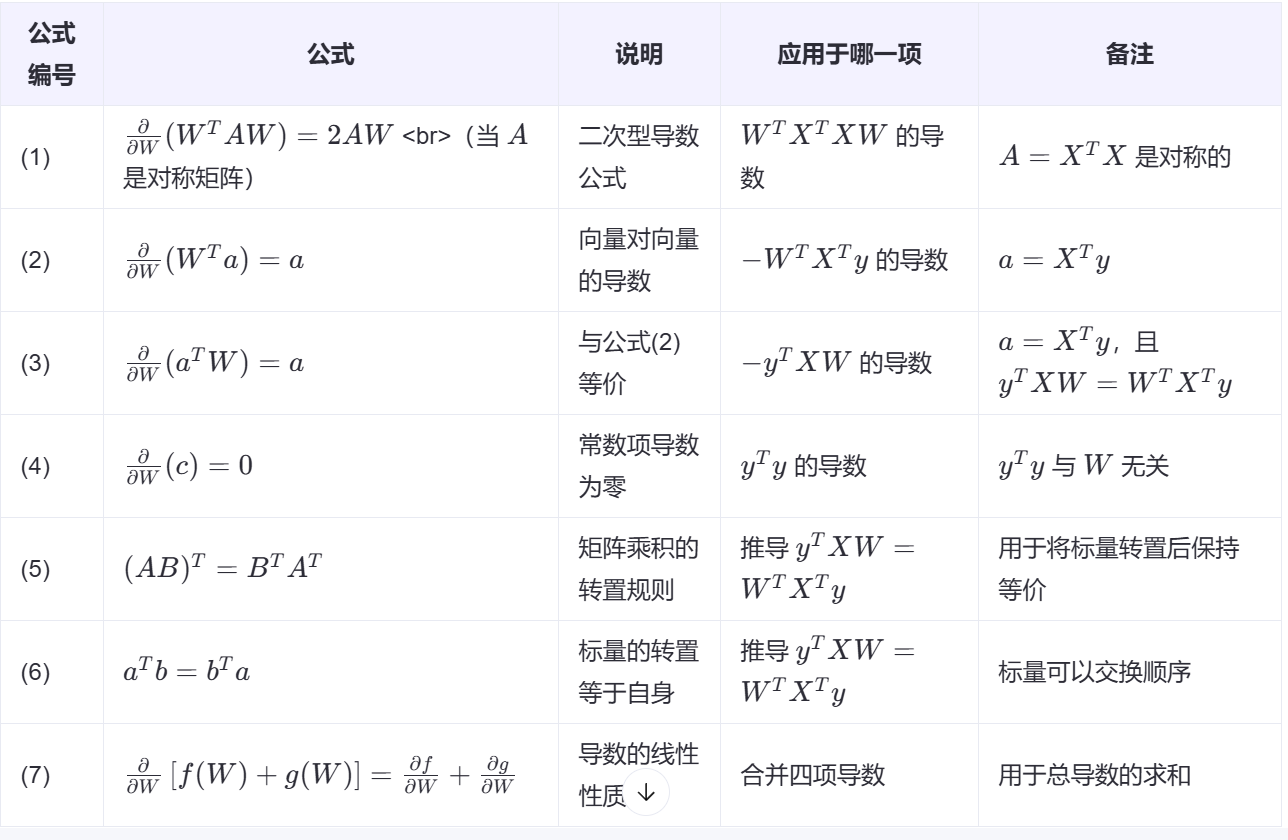
  • 多元线性回归损失函数求导过程


    \begin{aligned} loss &= \frac{1}{2}(WX-y)^T(WX-y)\\ loss'&= \frac{1}{2}((WX-y)^T(WX-y))’\\ &= \frac{1}{2}(W^TX^TXW-W^TX^Ty-y^TXW+y^Ty)'\\ &= \frac{1}{2}(2X^TXW-X^Ty-y^TX+0)\\ &= \frac{1}{2}(2X^TXW-2X^Ty)\\ &= X^TXW-X^Ty\\ \end{aligned}

    • 令导数loss'=0


    \begin{aligned} X^TXW-X^Ty &= 0 \\ (X^TX)^{-1}(X^TX)W &= (X^TX)^{-1}X^T\\ W &= (X^TX)^{-1}X^Ty \end{aligned}

  • 在 Scikit-learn 库中，LinearRegression类提供了普通最小二乘法（Ordinary Least Squares, OLS）的线性建模方法。该模型假设输出变量（y）与输入变量（X）之间存在线性关系，LinearRegression()方法是用来创建模型对象的，参数如下：

    参数名类型是否可选默认值含义说明
    fit_interceptbool是True- 如果为 True，模型将包含一个截距项（即当所有特征为 0 时的预测值） - 截距不受正则化影响（如使用正则化） - 会在特征矩阵中自动添加一列全为 1 的列（表示常数项）

    • 常用属性：

    属性名含义说明
    coef_系数估计值，即线性模型中每个特征的权重（斜率）
    intercept_截距估计值，即当所有特征值为 0 时模型的预测值（y轴截距）
    n_features_in_输入特征的数量（训练数据中特征的维度）
    feature_names_in_输入特征的名称（仅当输入数据具有列名时可用）
被爱学习指数抗压指数运动指数饮食情况金钱心态压力健康程度
014805-29-3339
-41064-14-2-148-114
-1-65-123-32-230
5-23105114-8126
-15-15-8-157-4-122-395
11-10-243-9-67-87
-1404-3510137422
-3-7-2-80-6-5-9-309
111481051081?
"""利用线性回归方法，计算出 karen 的健康程度API：from sklearn.linear_model import LinearRegression参数：fit_intercept：是否添加截距【偏置项】
"""
from sklearn.linear_model import LinearRegression
import numpy as np
​
# 数据集
data = np.array([[0, 14, 8, 0, 5, -2, 9, -3, 399],[-4, 10, 6, 4, -14, -2, -14, 8, -144],[-1, -6, 5, -12, 3, -3, 2, -2, 30],[5, -2, 3, 10, 5, 11, 4, -8, 126],[-15, -15, -8, -15, 7, -4, -12, 2, -395],[11, -10, -2, 4, 3, -9, -6, 7, -87],[-14, 0, 4, -3, 5, 10, 13, 7, 422],[-3, -7, -2, -8, 0, -6, -5, -9, -309]])
# 特征信息
X = data[:, :8]
# 结果
y = data[:, 8]
# 线性回归估计器 --- fit_intercept=True 表示使用截距
lr = LinearRegression(fit_intercept=True)
# 投喂
lr.fit(X, y)
# 输出权重参数和截距
print("权重参数：\n", lr.coef_)
print("截距：\n", lr.intercept_)
# 准备测试数据
karen = np.array([[15, 12, 10, -10, 5, 9, 5, 10]])
# 预测
result = lr.predict(karen)
print("预测结果：\n", result)
​

15.1、切线的斜率

切线的斜率分为几种情况：4 种情况，设切线的斜率为 k

  • k = 0：平行于 x 轴

  • k 不存在：垂直于 x 轴

  • k > 0：切线过第一和第三象限

  • k < 0：切线要过第二和第四象限

15.2、梯度下降思想

  • 如果我们按照之前的方程，去求梯度的方式求解最佳的w值，可能由于的不同的损失函数，导致求解出来的极值并不是最佳的w值

  • 如果我们的特征信息比如有1000个，那么需要去求解1000次偏导数？？？这个事情是可以做的，但是他会极大的影响计算机的计算效率

  • 所以针对于上述的两个问题，提出来了一个新的方案，来代替原来的方案去计算w的值，这个方案就叫梯度下降

  • 梯度下降的知识点一：针对于不同的特征之间，做不同的计算，比如特征有 w1,w2，分别求解w1,w2，优化w1,w2

  • 梯度表示的就是损失函数对于参数的偏导数

  • 梯度下降？为什么是下降？而不是上升？

    • 梯度下降是用于最小化损失函数，通过沿着损失函数梯度的反方向（即梯度下降方向）调整参数，逐步逼近损失函数的最小值，从而优化模型；而梯度上升用于最大化目标函数，方向相反，机器学习中通常需要最小化损失函数，所以常用梯度下降。

  • 梯度下降中切线斜率的意义，大小，正负

    • 切线斜率：在梯度下降中，切线斜率表示损失函数在当前点的局部变化率，反映了损失函数在该点附近的变化趋势和方向。它决定了参数更新的方向和步长，是梯度下降算法的核心依据。

    • 大小：切线斜率的大小（绝对值）表示损失函数在该点的变化快慢。

      • 斜率大：损失函数在该点变化剧烈，梯度下降时步长可以相对较大，参数更新速度较快。

      • 斜率小：损失函数在该点变化平缓，梯度下降时步长需要较小，避免越过最小值。

    • 正负：切线斜率的正负表示损失函数在该点的增减方向。

      • 斜率为正：损失函数在该方向上是增加的，梯度下降需要沿着相反方向（负方向）更新参数。

      • 斜率为负：损失函数在该方向上是减少的，梯度下降同样沿着相反方向（正方向）更新参数

  • 梯度下降中更新参数 w 的公式的理解：w = w - a*梯度

    • 从当前参数 w 出发，沿着梯度的反方向（即损失函数下降最快的方向）移动一步，步长由学习率 α 决定。

  • 梯度下降？以为我们在更新权重w的时候，需要找到最佳的w的值，那么就应该使用 w新 = w旧-a*梯度值，这里的梯度值看作是w点的切线的斜率，那么斜率就有正负，无论在左边还是右边都要往低处移动，所以我们就是按照往梯度下降的地方进行移动

  • 为什么可以使用数学解析式来实现权重的更新，为什么还需要使用梯度下降？

    • 计算复杂度的问题

    • W = (XTX)-1X^TY，这个 (XTX)-1一定可以执行吗？如果说一个矩阵可逆，需要满足det(矩阵)!=0，如果是 2x2 的矩阵，就是对角线的乘积的差不能等于0，如果等于0了称为奇异矩阵。但是呢我们使用梯度下降的思想，就可以完成这样的操作

  • 使用梯度下降思想之后，我们更新权重的公式就变成了

    • w 是原来的权重参数

    • a 是学习率

      • 如果学习率太大：每次更新 w 变化大，可能会发生震荡，反复横跳

      • 如果学习率太小：每次更新 w 变化小，但是可能进入局部最优解

      • 学习率的设置是一个非常重要的事情，一般情况下都是给上比较小的值，比如0.1 0.01 0.001，可以动态的改变的这个值

    • 梯度值就等于 w 这个点上的切线的斜率


w' = w - \alpha ·梯度值

15.3、全局最优解和局部最优解

全局最优解：目标函数（如损失函数）在整个参数空间中的最低点（最小值）。此时模型达到理论上的最佳性能。

局部最优解：在某个邻域内（参数空间的一个小区域），目标函数的局部最低点，但比全局最优解更高。

15.4、早停机制

  • 如果训练模型1000次，但是在500次-600次的时候，发现模型基本上已经收敛，更新不动了，那么模型训练就会自动停止

15.5、截距

对于线性方程而言，截距一般情况都是需要存在的，即使对计算效率产生影响，但是它的加入能够提升方程的泛化能力，如果没有截距，方程必须过原点，有的话可以不过原点

15.6、梯度下降方法

  • 指的是如何使用训练数据集来求解我们的梯度值，进而更新权重

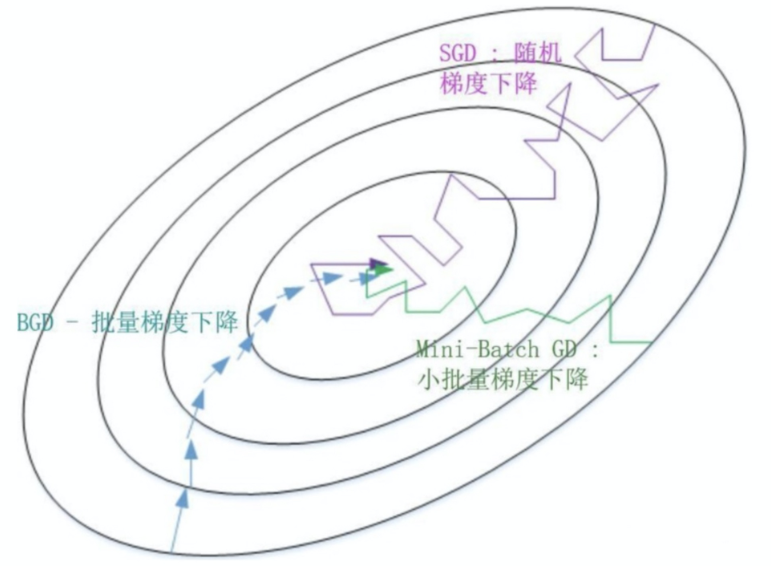
  • 批量梯度下降：每次计算梯度值的时候，使用全部的训练数据集去计算，然后取平均值

    • 好处：准确

    • 弊端：计算量大，因为每一次都需要计算处理全部数据集

  • 随机梯度下降：每一次计算梯度值的时候，随机选择一个训练数据集的样本，更新

    • 好处：快，计算量小

    • 弊端：不太准确，因为一个样本信息不能代表全部样本信息

  • 小批量梯度下降：上述两种办法的折中方法，就把每一个小批次（batch、batch_size）的数据集用来计算梯度值

    • 什么是批次：

  • 认识3个单词 ---- 假设训练数据集有 1000 个数据

epochsbatch(batch_size)
轮次，就是模型需要学习训练数据集多少次，如果设置为1，表示模型只需要去学习1000个数据 1 次他就是指的是，在每一个轮次中，分为多少次完成训练，这个多少次就去取决于设置的batch参数的大小，batch参数意义就是每一轮次中每一个小批次中取多少条数据训练，比如1000个数据，batch=16，就需要63次完成一次训练【1000/16向上取整】 如果这个参数设置过大，他根据数据集处理，需要更多的显存，如果你的计算机硬件设备跟不上，那么就会导致无法设置过大的batch，batch过大、过小都不好，一般选择2的倍数

  • 需要掌握的内容就是思想，能够描述出三种方案分别是如何进行的

  • 更新权重参数的步骤：假设以及初始化权重参数和学习率

    • 第一步：首先需要找到当前点【数据信息】的梯度值

    • 第二步：使用原来的权重参数值减去学习率乘以梯度值，得到新的权重值

    • 第三步：循环执行，知道epochs【自己设置的参数】结束

  • 为什么要用数据集去计算梯度值？

    • 数据集提供了梯度的无偏估计，平衡了计算效率和方向准确性，使模型能稳定地逼近真实最优解。

  • 损失函数怎么来的？

    • 计算预测值和真实值之间的差值

方法名称全称每次更新使用的数据量优点缺点
批量梯度下降Batch Gradient Descent (BGD)整个训练数据集- 梯度计算准确 - 收敛稳定- 计算开销大 - 数据量大时速度慢 - 不适合内存受限场景
随机梯度下降Stochastic Gradient Descent (SGD)单个样本- 更新频率高 - 训练速度快 - 有助于跳出局部最小值- 损失波动大 - 收敛路径曲折 - 难以达到精确最小值
小批量梯度下降Mini-Batch Gradient Descent (MBGD)小批量样本（如 32、64、128）- 平衡收敛速度与稳定性 - 利用向量化计算加速 - 实用性强- 需要调参（批量大小） - 若批量太小仍会波动，太大则变 BGD

  • 假设你有一个包含 1000 个样本的数据集：

方法每次更新使用的样本数每轮迭代更新次数
BGD1000 个1 次
SGD1 个1000 次
MBGD（batch size=32）32 个1000 / 32 ≈ 31 次
"""这里只是一个简单的案例，不考虑数据集，只是为了计算出来 w 更新的过程思路：对于方程 loss = loss(w_1)=(w_1-3.5)**2-4.5*w_1+10第一步：对loss求w1的偏导数 --- grad = 2w_1-11.5第二步：把上一个次w值，导入公式中，计算出来 grad第三步：计算新的w的值，w旧-学习率*grad第四步：循环更新。。。
"""
# 定义损失函数
def loss(w_1):return (w_1 - 3.5) ** 2 - 4.5 * w_1 + 10
# 求偏导
def grad(w_1):return 2 * w_1 - 11.5
# 初始化 w 值和学习率 a
w_1 = 10
a = 0.01
# 更新梯度
for i in range(10):w_1 = w_1 - a * grad(w_1)print(f"第{i+1}次更新的权重值为：{w_1}")
# loss(w_1,w_2)=(w_1-3.5)**2+(w_2-2)**2+3*w_1*w_2-4.5*w_1+2*w_2+20
# 定义损失函数
def loss(w_1, w_2):return (w_1-3.5)**2+(w_2-2)**2+3*w_1*w_2-4.5*w_1+2*w_2+20
# 求偏导
def grad_w1(w_1, w_2):return 2 * (w_1 - 3.5) + 3 * w_2 - 4.5
def grad_w2(w_1, w_2):return 2 * (w_2 - 2) + 3 * w_1 + 2
# 初始化 w 值和学习率 a
w_1 = 10
w_2 = 20
c = 1
b = 100
# 初始化学习率
a = c/b
# 更新梯度
for i in range(10):# w1 和 w2 分开更新w_1_ = w_1 - a * grad_w1(w_1, w_2)w_2 = w_2 - a * grad_w2(w_1_, w_2)w_1 = w_1_# 更新学习率a = c/(b+i)print(f"第{i+1}次更新的权重值为：{w_1},{w_2},学习率为：{a}")

随机梯度下降：

sklearn.linear_model.SGDRegressor()是用来实现梯度下降法线性回归模型

  • 参数

参数名类型默认值描述
lossstr'squared_error'损失函数，默认为均方误差。其他选项包括 'huber', 'epsilon_insensitive' 等
fit_interceptboolTrue是否计算偏置项（截距）
eta0float0.01初始学习率（当使用 constant 或 invscaling 时）
learning_ratestr'invscaling'学习率调度方式： - 'constant': eta = eta0 学习率为eta0设置的值，保持不变 - 'optimal': eta = 1.0 / (alpha * (t + t0)) - 'invscaling': 与迭代次数的幂成反比，eta = eta0 / pow(t, power_t) - 'adaptive': 初始为 eta0，在收敛时逐步减小，
max_iterint1000最大迭代次数（即 epochs 数）
shuffleboolTrue是否在每次迭代前打乱训练数据
penaltystr or None'l2'正则化方式： - 'l2': L2 正则化（默认） - 'l1': L1 正则化（稀疏性） - 'elasticnet': L1+L2 混合正则化 - None: 不使用正则化
tolfloat1e-3定义了损失函数或权重系数的变化需要小到何种程度时，算法可以认为已经达到了收敛状态，并停止进一步的迭代，默认值是 1e-3（0.001）

  • 主要属性

属性名描述
coef_训练后的模型权重系数（特征对应的参数）
intercept_训练后的偏置项（截距）
"""api：from sklearn.linear_model import SGDRegressor
"""
import numpy as np
from sklearn.linear_model import SGDRegressor
from sklearn.datasets import fetch_california_housing
from sklearn.model_selection import train_test_split
​
# 加载加利福尼亚数据集
data = fetch_california_housing(data_home="./")
np.set_printoptions(suppress=True)
# X 和 y
X = data.data
print("特征信息：\n", data.feature_names)
print(X[:5])
y = data.target
# 划分数据集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
# 创建估计器
"""参数：loss：损失函数penalty：正则化方案，l1 l2 elasticnet[混合l1和l2]alpha：正则化的惩罚因子 0.0001eta0：初始化学习率，默认值 0.0001fit_intercept：截距，偏置项max_iter：最大的训练次数
"""
sgdr = SGDRegressor(loss="squared_error", penalty="l2", alpha=0.0001, eta0=0.01, fit_intercept=True, max_iter=1000)
# fit
sgdr.fit(X_train, y_train)
# 模型得分
print(sgdr.score(X_test, y_test))
# 权重参数矩阵数量=特征信息数量
print("权重参数：\n", sgdr.coef_)
# 截距，偏置项
print("截距：\n", sgdr.intercept_)
# 预测
test = np.array([[8, 35, 8, 0.8, 300, 2.5, 35, -122]])
print("预测结果：\n", sgdr.predict(test))
​

小批量梯度下降MBGD:

  • 还是使用sklearn.linear_model.SGDRegressor()，只是训练时我们分批次地训练模型，调用partial_fit函数训练会直接更新权重，而不需要调fit从头开始训练。通常情况下，我们会将数据分成多个小批量，然后对每个小批量进行训练

  • partial_fit 是 SGDRegressor中的一个重要方法，用于增量式训练模型，也称为在线学习，不同于 fit() 方法一次性使用全部数据训练模型，partial_fit 允许你分批次（mini-batch）地训练模型，即每次只用一部分数据更新模型参数，参数说明

参数类型描述
Xarray-like, shape (n_samples, n_features)训练样本特征数据
yarray-like, shape (n_samples,)目标值（标签）

  • 注意事项：

    • 首次调用 partial_fit 前不需要调用 fit()，可以直接使用

    • 多次调用 partial_fit 会持续更新模型参数，而不是重新训练

    • partial_fit 不会重置模型参数，所以如果你想重新训练，需要显式地创建一个新的模型实例

    • 如果 fit_intercept=True（默认），则 partial_fit 会自动更新 intercept_

    • 在使用 partial_fit 时，不会自动打乱数据（unlike fit() 中的 shuffle=True 默认行为），需要手动打乱数据批次以保证收敛效果

    • 完整地遍历一次训练集，叫做一个 epoch（训练轮次）

    • 每个 epoch 中，你要处理 n_batches 个 mini-batch

    • 每处理一个 mini-batch，就调用一次 partial_fit()（或类似方法）来更新模型参数

"""api：from sklearn.linear_model import SGDRegressor
"""
import math
import numpy as np
from sklearn.linear_model import SGDRegressor
from sklearn.datasets import fetch_california_housing
from sklearn.model_selection import train_test_split
​
# 加载加利福尼亚数据集
data = fetch_california_housing(data_home="./")
np.set_printoptions(suppress=True)
# X 和 y
X = data.data
y = data.target
# 划分数据集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
# 创建估计器
sgdr = SGDRegressor(loss="squared_error", penalty="l2", alpha=0.0001, eta0=0.01, fit_intercept=True, max_iter=2)
"""小批量梯度下降算法，我们需要知道以下几个参数：1、多少个轮次【epochs】2、批处理大小【batch】3、每个轮次分为多少个批次【math.ceil(len(数据集大小)/batch)】4、假设数据集有1000个，batch=16，每1个epoch需要33个小批次才把数据集训练完每一个小批次取得数据都是不一样的需要计算每个小批次获取数据集中数据的起始位置和结束位置start_index = (当前循环的小批次) * batch end_index = start_index + batch从数据集中切片的方式，取出当前批次的数据，训练
"""
# 数据集中数据的个数
train_length = len(X_train)
# 设置 batch 大小
batch = 14
# 每一个轮次中分成多少个批次完成
batch_num = math.ceil(train_length / batch)
# 训练多少epochs
epochs = sgdr.max_iter
print("数据集大小：", train_length)
print("每个轮次中分成多少个批次：", batch_num)
print("训练的轮次：", epochs)
# 分批次训练数据
for epoch in range(epochs):# 可以在这里加上打乱数据集的代码 ----# 批次循环for i in range(batch_num):# 数据开始的索引值start_index = i * batch# 数据结束时的索引值 ---- 严谨一点应该考虑最后一次的数据取值情况end_index = start_index + batch# 从数据集切片，取出当前批次的数据 ---- 如果写成了X_train会导致数据集的内容发生变化了batch_X_train = X_train[start_index:end_index]batch_y_train = y_train[start_index:end_index]# 使用当前批次的数据投喂模型 --- 不使用 fit --- 使用 partial_fit 分批次训练sgdr.partial_fit(batch_X_train, batch_y_train)print(f"第{epoch}/{epochs}次训练完成")
​
# 模型得分
print(sgdr.score(X_test, y_test))
# 权重参数矩阵数量=特征信息数量
print("权重参数：\n", sgdr.coef_)
# 截距，偏置项
print("截距：\n", sgdr.intercept_)
# 预测
test = np.array([[8, 35, 8, 0.8, 300, 2.5, 35, -122]])
print("预测结果：\n", sgdr.predict(test))
​

15.7、过拟合和欠拟合

欠拟合：

  • 欠拟合是指模型在训练数据上表现不佳，同时在新的未见过的数据上也表现不佳。这通常发生在模型过于简单，无法捕捉数据中的复杂模式时。欠拟合模型的表现特征如下：

    • 训练误差较高

    • 测试误差高

    • 模型可能过于简化，不能充分学习训练数据中的模式

  • 造成欠拟合的主要原因是由于没有选择好合适的特征值

  • 解决欠拟合的方法包括：

    • 增加模型的复杂度，如增加模型的层数、节点数或特征数

    • 寻找更丰富的特征集合

过拟合：

  • 过拟合是指模型在训练数据上表现得非常好，但在新的未见过的数据上表现较差。这通常发生在模型过于复杂，以至于它不仅学习了数据中的真实模式，还学习了噪声和异常值。过拟合模型的表现特征如下：

    • 训练误差非常低

    • 测试误差较高

    • 模型可能过于复杂，以至于它对训练数据进行了过度拟合

  • 解决过拟合的方法包括：

    • 增加训练数据量，以减少噪声和异常值的影响

    • 使用正则化技术，如 L1 正则化和 L2 正则化，来约束模型参数的大小

    • 简化模型复杂度，如减少模型的层数、节点数或特征数

    • 使用交叉验证等技术来选择最佳的模型参数

正则化：

正则化就是防止过拟合，增加模型的鲁棒性，鲁棒是 Robust 的音译，也就是强壮的意思。就像计算机软件在面临攻击、网络过载等情况下能够不死机不崩溃，这就是软件的鲁棒性，鲁棒性调优就是让模型拥有更好的鲁棒性，也就是让模型的泛化能力和推广能力更加的强大

  • 在之前学习的公式y=w^Tx中，如果 x 中的某一个数据异常，那么就会被 w 参数放大，但是 w 也不能太小（趋近0）太小的话模型就没有意义。这个时候就需要使用到正则化来保证容错率以及准确率

  • 正则化的本质就是牺牲模型在训练集上的正确率来提高推广、泛化能力，W 在数值上越小越好，这样能抵抗数值的扰动。同时为了保证模型的正确率 W 又不能极小。故而人们将原来的损失函数加上一个惩罚项，这里面损失函数就是原来固有的损失函数，比如回归的损失函数通常是 MSE、分类的损失函数通常是 cross entropy 交叉熵，在损失函数后加上一部分惩罚项来使得计算出来的模型 W 相对小一些来带来泛化能力

  • 常用的惩罚项有 L1 正则项、L2 正则项：

    • L_1=||w||_1=\sum_{i=1}^n|w_i|，

    • L_2=||w||_2=\sqrt{\sum_{i=1}^n(w_i)^2}，不常用，计算复杂

    • L_2^2=||w||_2^2=\sum_{i=1}^n(w_i)^2，更常用形式，它更容易计算梯度（导数简单），也更容易优化

15.8、重要内容

  • 什么是梯度？

    • 梯度就是一个向量，有大小有方向，梯度的大小就是当前点的斜率【偏导数的值】，梯度的方向就是函数增长最快的方向

  • 方向导数

  • 梯度下降为什么要使用？

    • 梯度下降=“用一阶信息+线性时间复杂度” 去逼近一个“足够好的局部最优”，在高维、非凸、大数据场景里，它几乎是目前唯一现实可行的选择。

  • 梯度下降的目的？

    • 在可接受的时间内，把损失函数磨到足够低的局部极小值，从而让模型在未见数据上表现最好”

    • 梯度下降不是为了“追求完美”，而是为了“在有限算力下，把损失压到足够低且不过拟合”

  • 使用梯度下降更新权重参数的公式

    • 梯度下降的公式：gradient 代表梯度，α 代表学习率，n 表示第几次梯度下降

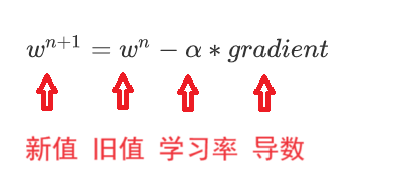
  • 学习率：比如你想下山，你走一步的步长就理解为学习率，学习率过大，可能你一下子就走到了对面那座上的山腰，如果学习率太小，那么你要花费很多事件才可以走到山脚【一般是0.01】

  • 梯度值如何计算的？偏导数在某一个点的值

    • 在哪一个点来计算这个梯度值？权重参数理解为就是一个向量，他又目前的方向，这个点就是这个权重参数当前所在的位置

    • 我们当前如何权重是w，那么我们是不是可以基于我们的w计算出来预测值，进而计算出来损失函数，我们要最小化损失函数，那么就相当于去找到权重参数的最优解，那么在求解梯度的过程中，梯度值 = 损失函数对于某一个特征权重的偏导数

    • 损失函数值的计算依赖于什么？依赖于真实值和当前的w权重计算出来的预测值

    • 我们想要最小化损失函数，是不是应该使用当前的权重去和数据集计算当前的预测值，然后和真实值之间计算损失值

    • 所以梯度值的计算就依赖于数据集中的内容

  • 三种梯度下降的方法 --- 求解梯度值的时候使用的数据集的样本数量

    • BGD（批量梯度下降）

    • SGD（随机梯度下降）

    • mBGD（小批量梯度下降）

方法名称全称每次更新使用的数据量优点缺点
批量梯度下降Batch Gradient Descent (BGD)整个训练数据集- 梯度计算准确 - 收敛稳定- 计算开销大 - 数据量大时速度慢 - 不适合内存受限场景
随机梯度下降Stochastic Gradient Descent (SGD)单个样本- 更新频率高 - 训练速度快 - 有助于跳出局部最小值- 损失波动大 - 收敛路径曲折 - 难以达到精确最小值
小批量梯度下降Mini-Batch Gradient Descent (MBGD)小批量样本（如 32、64、128）- 平衡收敛速度与稳定性 - 利用向量化计算加速 - 实用性强- 需要调参（批量大小） - 若批量太小仍会波动，太大则变 BGD

  • 假设你有一个包含 1000 个样本的数据集：

方法每次更新使用的样本数每轮迭代更新次数
BGD1000 个1 次
SGD1 个1000 次
MBGD（batch size=32）32 个1000 / 32 ≈ 31 次

  • 梯度下降的三种方法，主要就是体现在梯度下降步骤过程中的第二步中

15.9、范数

l1： 数学公式：re = ||X||/(||X1|| + ... + ||Xn||) 每一条数据的值的和为 1

l2：【掌握】 数学公式：re = ||X||/sqrt(||X1||^2 + ... + ||Xn||^2)每一条数据集的值的平方和等于1 max： 数学公式：re = max(X,1)每一条数据中的值最大的一个为 1

15.10、几个名词

泛化能力：泛化能力 = 模型在未见过的数据上表现好的能力，而非只在训练集上“死记硬背”

泛化能力是机器学习模型的终极目标：

“让模型在没见过的数据上也能准确预测，而不是在训练集上‘表演’

鲁棒性：当输入数据偏离训练分布或遭受扰动、攻击、异常值时，模型依然保持性能稳定、输出可靠的能力

与泛化能力的区别 • 泛化：在“未见但同分布”数据上表现好。 • 鲁棒：在“分布偏移、对抗扰动、自然损坏”上依旧表现好。 例：在 ImageNet-C（自然腐蚀图像）上，鲁棒模型准确率下降 <10%，普通模型下降 >30%。

十六、岭回归算法

  • 岭回归（Ridge Regression）是一种线性回归技术，它通过在损失函数中加入一个正则化项来解决多重共线性问题。岭回归在普通最小二乘法的基础上添加了一个 L2 范数惩罚项，这样可以减小模型的方差，从而提高模型的泛化能力

    • sklearn.linear_model.Ridge()是 sklearn 提供的实现岭回归的一个模型，参数如下

    参数名类型默认值含义说明
    alphafloat1.0正则化强度，即 λ。值越大，正则化作用越强，防止过拟合。
    fit_interceptboolTrue是否计算偏置项（截距 intercept_）。若为 False，则数据应已中心化。
    solverstr'auto'求解系数的方法，可选：'auto', 'svd', 'cholesky', 'lsqr', 'sparse_cg', 'sag', 'saga', 'lbfgs'。默认自动选择最优方法。
    normalizeboolTrue是否对特征进行标准化（均值为0，方差为1）。如果在特征工程中已标准化，应设为 False。
    max_iterintNone最大迭代次数，仅在使用迭代求解器（如 'sag', 'saga', 'lsqr'）时有效。默认根据数据自动选择。

    • solver 可选值及其适用场景

    solver 名称适用场景说明
    'auto'默认自动根据数据类型和问题选择最合适的求解器
    'svd'小数据集使用奇异值分解，适合特征数较少的数据
    'cholesky'中等数据集使用 Cholesky 分解，数值稳定但计算较慢
    'lsqr'大数据集支持稀疏矩阵，迭代法，推荐用于大规模数据
    'sparse_cg'大数据集共轭梯度法，适合稀疏数据
    'sag'大数据集随机平均梯度下降，适合大数据和L2正则
    'saga'大数据集'sag' 的改进版，支持 L1 正则
    'lbfgs'大数据集优化算法，适用于多元逻辑回归等模型

    • 属性

    属性名含义
    coef_模型训练后的权重系数（即回归系数 w）
    intercept_偏置项（截距），当 fit_intercept=True 时存在
"""就是在线性回归的损失函数后边加上了l2正则化项目的：提高模型的鲁棒性
"""
import numpy as np
from sklearn.linear_model import Ridge
from sklearn.datasets import fetch_california_housing
from sklearn.model_selection import train_test_split
​
"""写代码，一定是写一步测试一步，不要想着把代码写完了再来运行程序写代码的时候，尽可能的写上注释内容
"""
data = fetch_california_housing(data_home="./")
# 获取数据
X = data.data
y = data.target
# 划分数据集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
# 创建估计器
"""参数：alpha：正则项力度，就是正则项的因子，默认 1.0fit_intercept：截距normalize：归一化
"""
r = Ridge(alpha=0.1, fit_intercept=True)
# fit
r.fit(X_train, y_train)
print("权重参数：\n", r.coef_)
print("截距参数：\n", r.intercept_)
# 模型得分
print("模型得分：\n", r.score(X_test, y_test))
# 预测
test = np.array([[8, 35, 8, 0.8, 300, 2.5, 35, -122]])
print("预测结果：\n", r.predict(test))

http://www.dtcms.com/a/342188.html

相关文章：

  • 以往内容梳理--HRD与MRD
  • 《深入探索 Java IO 流进阶：缓冲流、转换流、序列化与工具类引言》
  • 事件驱动流程链——EPC
  • Metrics1：Intersection over union交并比
  • tail -f与less的区别
  • Python Excel 通用筛选函数
  • 【C++】模板（进阶）
  • Rancher 管理的 K8S 集群中部署常见应用（MySQL、Redis、RabbitMQ）并支持扩缩容的操作
  • ubuntu编译ijkplayer版本k0.8.8（ffmpeg4.0）
  • Spring Boot整合Amazon SNS实战：邮件订阅通知系统开发
  • 将windows 的路径挂载到Ubuntu上进行直接访问
  • C++---辗转相除法
  • VB.NET发送邮件给OUTLOOK.COM的用户,用OUTLOOK.COM邮箱账号登录给别人发邮件
  • Azure的迁移专业服务是怎么提供的
  • 带有 Angular V14 的 Highcharts
  • Transformer在文本、图像和点云数据中的应用——经典工作梳理
  • 【解决方案系列】大规模三维城市场景Web端展示方案
  • C++STL-stack和queue的使用及底层实现
  • 阿里云搭建flask服务器
  • 2021年ASOC SCI2区TOP，改进遗传算法+自主无人机目标覆盖路径规划，深度解析+性能实测
  • Java 16 新特性及具体应用
  • Redis 奇葩问题
  • Python break/continue
  • 嵌入式C语言和数据结构面试题
  • 2025-08-21 Python进阶3——模块
  • 信创自主可控新标杆：RustFS如何用内存安全架构重构数据主权防线？
  • Binlog Server守护MySQL数据0丢失
  • RabbitMQ：技巧汇总
  • Windows下RabbitMQ完整安装指南
  • 云原生俱乐部-k8s知识点归纳（6）