当前位置：首页 > news >正文

Metrics1：Intersection over union交并比

news 2025/8/22 6:51:05

参考：https://en.wikipedia.org/wiki/Jaccard_index

1，定义：

Intersection over union（交并比），又称之为**Jaccard index（Jaccard指数）。**

衡量样本集相似性和多样性的统计量，

衡量有限非空样本集之间的相似性

（1）IoU

总的来说，如果想要在机器学习任务中计算1个IoU，我们需要两个数据：

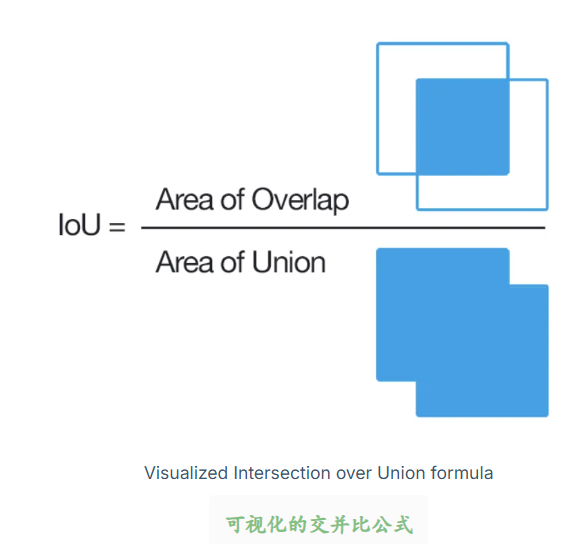
另外需要注意的是，在目标检测、实例分割或语义分割等计算机视觉任务中，不直接计算预测的 (x, y) 坐标与真实标注的 (x, y) 坐标之间的差异，而是计算交集（Intersection）和并集（Union）。

这在很大程度上是由于需要学习的任务所决定的：

1. 模型预测的不确定性

预测坐标不完美：在实际应用中，模型预测的边界框或掩码的坐标几乎不可能与真实标注完全一致。由于模型的参数、训练数据的有限性以及模型的泛化能力等因素，预测结果总会存在一定的偏差。
需要鲁棒性评估：直接比较 ( (x, y) ) 坐标对会过于敏感，即使预测结果与真实标注非常接近，也可能因为微小的偏差导致评估结果不佳。而通过计算交集和并集，可以更鲁棒地评估模型的性能。

2. 重叠区域的意义

重叠区域的重要性：在目标检测和分割任务中，我们更关心的是预测结果与真实标注之间的重叠程度。如果预测的边界框或掩码与真实标注有较大的重叠区域，说明模型对目标的定位和分割是较为准确的。
奖励重叠：通过计算交集和并集，可以奖励那些与真实标注有较大重叠的预测结果。这比直接比较 ( (x, y) ) 坐标对更能反映模型对目标的识别和定位能力。

3. 交并比（IoU）的直观性和可解释性

直观性：交并比（IoU）是一个非常直观的指标，它通过计算预测结果与真实标注的重叠面积与并集面积的比值，直接反映了预测结果与真实标注的匹配程度。IoU 的值在 0 到 1 之间，值越接近 1，说明预测结果越准确。
可解释性：IoU 的计算公式简单，容易理解和解释。它不需要复杂的数学背景，即使是非专业人士也能快速理解其含义。

4. 多目标情况的处理

多目标的独立评估：在多目标检测或分割任务中，每个目标都有自己的真实标注和预测结果。通过计算每个目标的 IoU，可以独立评估每个目标的预测质量，而不需要将所有目标的预测结果合并成一个统一的指标。
平均 IoU：通过计算所有目标的 IoU 平均值，可以得到整个测试集的综合评估结果，这比直接比较每个目标的 ( (x, y) ) 坐标对更加全面和有效。

当然，这个指标其实和平均精度均值（mAP）相关，而后者，

平均精度均值（mAP）是目标检测任务中常用的综合评估指标，它依赖于 IoU 的计算。通过计算不同 IoU 阈值下的平均精度，可以更全面地评估模型的性能。

简而言之，计算IoU指标的一般步骤如下：

然后就是多目标比较任务，只需简单地设置每一个目标设置任务。

至于解释，其实很简单，在 IoU 的情况下，指标值的解释很直接。重叠越大，分数越高，结果越好。

我们还是以计算机视觉中的经典任务：目标识别为例进行可视化解释：

一般的经验是，将 IoU > 0.95 视为优秀分数，IoU > 0.7 视为良好分数，其他分数则视为较差分数。

也就是（0.95,0.7）划分3类：excellent、good、poor。

当然，实际处理的时候，还是根据自己的逻辑和任务需求设置不同的阈值。

（2）Jaccard index：拓展（更数学地）

很好理解，其实就是交集面积比上并集面积。

交并比（IoU），也称为Jaccard指数，是分割、目标检测和跟踪（segmentation, object detection and tracking）等任务最流行的评估指标（evaluation metric），

分割比如说实例分割或语义分割任务（Instance Segmentation, or Semantic Segmentation）

这些都是计算机视觉的经典任务。

目标检测由两个子任务组成：定位（localization），即确定目标在图像中的位置，

分类（classification），即为该目标分配一个类别。

和IoU相关的是定位任务，目标检测中的定位（localization）目标是在场景中的目标周围绘制一个二维边界框。

很容易理解，model能够绘制一个预测的边界框，框中的object是model认为定位出来的object；

而真实object也有一个边界框，也就是ground-truth，

那么两个box两个框之间就有面积交集以及并集，也就有了model定位指标IoU。

其中关于概率测度部分：

在前面提到的 Jaccard 指数和距离的定义中，概率测度可以用来衡量两个事件的相似性和不相似性，

简单理解测度，可以参考我之前的一个博客https://blog.csdn.net/weixin_62528784/article/details/150592821?sharetype=blogdetail&sharerId=150592821&sharerefer=PC&sharesource=weixin_62528784&spm=1011.2480.3001.8118

具体来说：

共同缺失的特征是不会被考虑在内的。

2，延伸比较

（1） simple matching index (SMC)简单匹配指数

参考：https://en.wikipedia.org/wiki/Simple_matching_coefficient

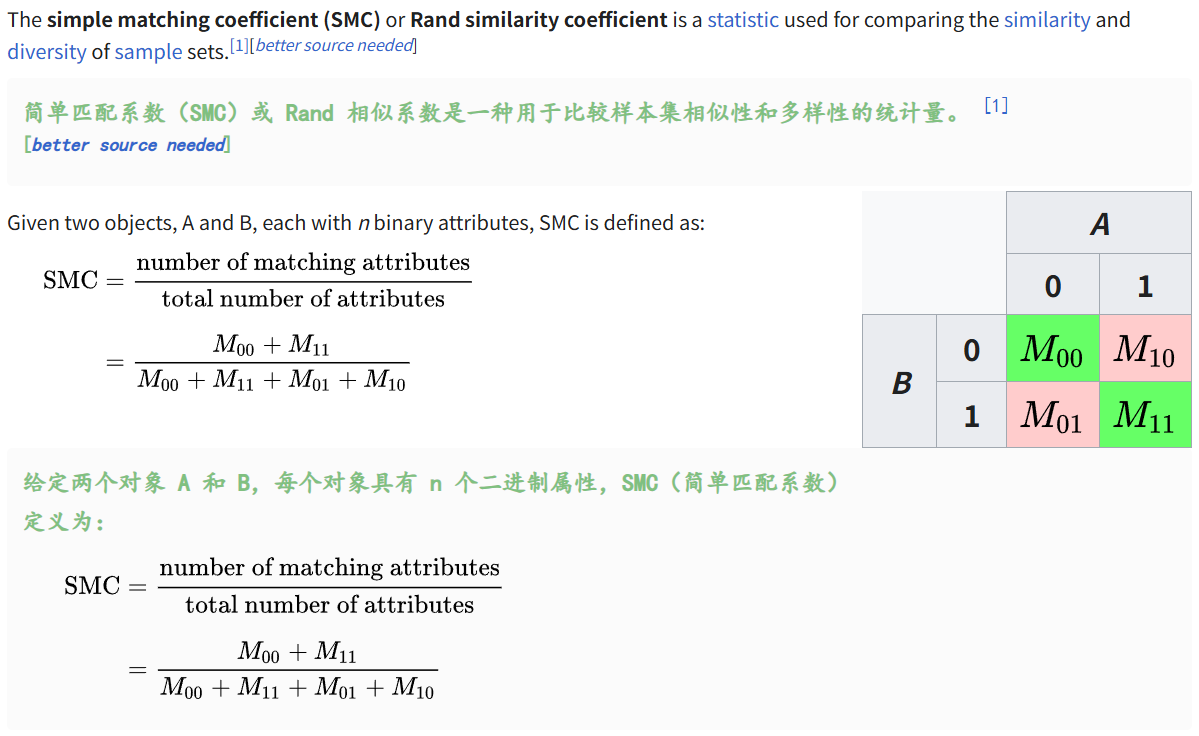
其实就是IoU的定义上，对于其中的都为0的attribute，在分子分母也计算在内。

本质上其实很容易类比，

很多distance metrics都是1-相似性，然后获取距离的度量。

（2）加权 Jaccard 相似性和距离

然后就是在不同的数学结构（比如说向量、函数以及集合-可测集）上定义Jaccard相似性指数以及距离

1️⃣向量上的Jaccard相似性指数和距离

定义上维度相同，且所有维度元素均为非负实数，那就可以对每一个index做一个pairing。

通过比较两个向量的对应元素的最小值和最大值来衡量它们的相似性，分子是pairing比较中min分量之和，分母是max分量之和。

2️⃣函数上的Jaccard相似性指数和距离

类比向量，离散的求和、连续的在测度上积分。

3️⃣集合上的Jaccard相似性指数

其实集合上的定义，就是最前面一开始的定义：

然后集合的定义，可以和函数的定义统一在一起：两个可测集合A/B在测度miu下的Jaccard相似性指数，为其特征函数的Jaccard相似性指数。也就是说

理解起来也很简单，其实就是将集合的交集和并集的大小通过特征函数的逐点最小值和最大值来计算，

从而统一集合、向量、函数的Jaccard相似性指数的定义。

首先需要理解特征函数：其实就是成员判断函数，可以简单理解为isin，或者是is a member of的定义：

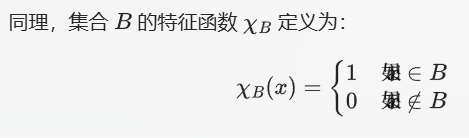
然后特征函数，就可以用上面2️⃣的定义来计算Jaccard相似性指数，

当然，因为这里函数x的取值是离散的，那就是类比1️⃣的定义来计算。

然后就可以通过特征函数来理解Jaccard相似性指数，

首先集合里的交集和并集（大小，size），就可以使用特征函数表示：

很容易就可以归并为前面的非加权距离指标，因为分子取min，只有（1,1）配对时才有值，其余都是0，包括前面说的M00，然后分子的话，其实就是在（0,1）、（1,0）或者是（1,1）时就会有取值，只有（0,0）时才没有值。

并集的大小，同样考虑了00不取的情况。

然后就可以通过特征函数计算Jaccard相似性指数，

其实就是特征函数的（0,1）来表征并计算序列的size。

其实上面的定义，在整体上并没有体现出weight权重的概念，

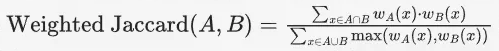
以分子为例，其实（0,1）比较特殊，（0,1）之间的乘法计算结果其实是和取min函数在结果上是一致的，因为一共就是4种pairing的组合。

然后权函数，其实也可以从特征函数进一步推广。

（3）Jaccard 相似性系数和加权 Jaccard 相似性系数的比较

本质上衡量两个集合相似度的指标，只不过在计算方式上有点区别，但同时也有点联系。

首先是定义上，

非加权的，其实就只看交集、并集size；

加权的，其实在挑选元素上，还是选取交集、并集，但是不仅仅是简单的看集合本身的形式（size），

还看集合中元素的性质，也就是对元素的权重值，也有一个估量就是考虑；

分子是元素权重的乘积，分母是权重的一个取max。

区别

联系

其实这个很容易就可以运用到计算生物学的序列分析上，

所谓权重，我们以蛋白质序列为例，对于每一个氨基酸，

氨基酸突变频率、进化距离、保守性，或者是随便拿一个理化性质参数（feature）——都可以在其参数空间的取值中量化每一个氨基酸的重要性，

包括最原始的序列比对，BLOSUM以及PAM等点突变构建的参数矩阵，

其实weight权重这个概念或者说思想，应该在生物序列分析中非常常见。

（4）概率Jaccard相似性和距离

（5）概率Jaccard指数的最优性

（6）Tanimoto相似性和距离

本质上是定义了一系列feature、attributes，然后构造了待比较对象的0、1序列（向量）

一些其他定义，

这里声明一点：所谓的ditance metric，在机器学习的场景下，很容易误用。

判断一个metric，能不能够用来定义为距离，需要满足一些最基本的性质。

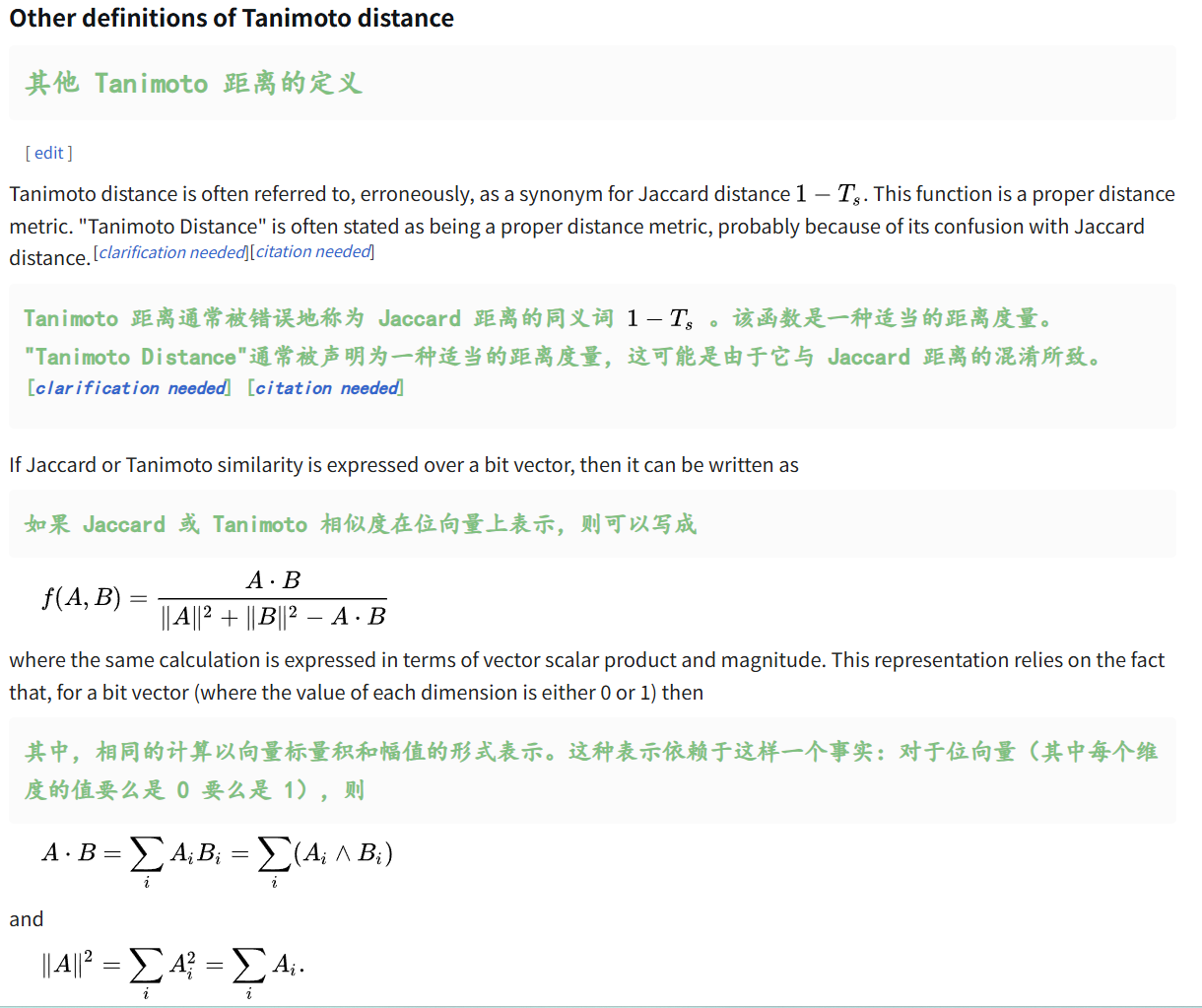
（7）二分类问题中的Jaccard指数（的直观可视化）

这个其实可以很直观的进行理解，

TP就是预测与真实符合，即红绿框内的面积；

FP是真实为阴性，却被预测为阳性，其实就是红-绿的差集；

FN是真实为阳性，却被预测为阴性，其实就是绿-红的差集。

其实就是分子、分母面积的拆分，对应到二分类问题的混淆矩阵上（毕竟TP/FP/FN等指标也是从混淆矩阵中推导出来的）。

3，implementation实现

（1）如果是在numpy中：

import numpy as np# 定义1个平滑参数，其实就是伪计数pseudocount，避免零除操作
SMOOTH = 1e-6# 定义交并比函数
def IoU_numpy(outputs:np.array, labels:np.array):"""Args:outputs: 模型的输出，形状为 (batch_size, num_classes, height, width)labels: 真实标签，形状为 (batch_size, num_classes, height, width)"""# 假设我们有一个批量大小为N的图像分割任务，然后模型的输出和标签的形状为（N,C,H,W）# 处理输入数组# 移除长度为1的维度，从（N,1,H,W）变为（N,H,W）outputs = outputs.squeeze()# 计算交集# 按位与&操作，计算交集，结果是获取1个bool数组，形状为（N,H,W），然后再sum(axis=(1,2)) 对每个样本按照第1、2维（也就是高度和宽度）进行求和，也就是对每个样本的交集进行求和，此时结果的形状为（N，）intersection = (outputs & labels).sum(axis=(1,2)) # 计算并集# 按位或|操作，计算并集，同样bool数组，形状为(N,H,W)，然后再对每个样本的并集进行求和，此时结果的形状为（N，）union = (outputs | labels).sum(axis=(1,2))# 计算IoU# IoU = 交集 / 并集，注意要加上平滑参数，避免除零错误# 也是一个逐元素的计算，结果的形状和输入相同iou = (intersection + SMOOTH) / (union + SMOOTH)# 对IoU指标进行一些数据处理，使其值映射到一个离散的范围# ⚠️⚠️⚠️这里的数据处理见仁见智，仅代表个人观点，注意，仅作为草稿示范，一些参数选取不代表一般情况！！！！# 先将IoU值进行缩放和平移iou_scaled = 20*(iou - 0.7)# 再进行阈值化,比如说任何＜0的值都设为0，＞10的值都设为10，就是将值的范围被限制在【0,10】中iou_thresholded = np.clip(iou_scaled, 0, 10) # 再进行取整，然后/10，将范围从【0,10】映射到【0,1】threshold = np.ceil(iou_thresholded) / 10return threshold# 或者返回thresholded.mean()

简单来说，以图像识别的计算机视觉任务为例，

图片的形状数据，通常可以使用一个多维数组来表示，比如说是(N, C, H, W)：

大致的维度解释意思如下：

N：批量大小（Batch Size），表示一次处理的图片数量，可以简单理解为样本数。
C：通道数（Channels），表示每张图片的通道数，比如说彩色图片就是RGB的3通道，然后灰白图片就是1通道（灰度图，每个像素只有1个值，要么是0要么是1，表示亮度；彩色图，每个像素有3个值，分别表示红绿蓝通道的强度）。
H：高度（Height），表示图片的垂直像素数。
W：宽度（Width），表示图片的水平像素数。

假设我们有一个批量大小（也就是样本数目）为N的图像分割任务，然后每张图像的高度为H，宽度为W、

通常，模型的输出和标签的形状为(N, C, H, W)。

当然，C只是我们这里的一个参数，具体指代的是什么，其实见仁见智。

如果是图像分割任务，那么每一个像素点其实就通常会被分配到一个特定的类别，比如说一个二分类的任务（比如说图片的背景和前景），每个像素点的值可以是0或1，在多分类任务中，每个像素点的值可以是0到C-1，C这里指代类别数，也就是class number。

通道的理解，channel，可用来表示图像的多维信息，在图像分割中，输入图像可能有多个通道，但预测结果和标签通常是一个单通道的二维数组，其中每个像素值表示的是类别标签（当然，channel值我们可以通过增加数组的维度，添加上去）。

假设我们有两个形状为3x3的图像image，分别表示预测结果和真实标签：

import numpy as np# 预测结果
outputs = np.array([[0, 1, 0],[1, 1, 1],[0, 1, 0]
])# 真实标签
labels = np.array([[0, 1, 0],[1, 0, 1],[0, 1, 0]
])

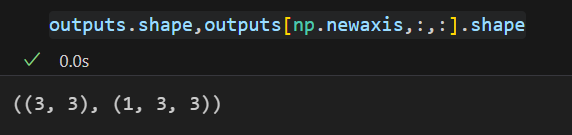
# 前面设计的函数用于处理批量数据，squeeze操作可加可不加
# 我们这里还是将单个图像扩展为一个批量，形状为（1,H,W）
outputs = outputs[np.newaxis,:,:]
labels = labels[np.newaxis,:,:]
IoU_numpy(outputs=outputs, labels=labels)

当然，对于iou的数据处理也不是必须的：直接按位与、或运算，然后再sum

# 1. 计算交集 (按位与 &)
intersection_matrix = outputs & labels
print("交集矩阵 (outputs & labels):")
print(intersection_matrix)
print(f"交集像素数: {intersection_matrix.sum()}")# 2. 计算并集 (按位或 |)  
union_matrix = outputs | labels
print("\n并集矩阵 (outputs | labels):")
print(union_matrix)
print(f"并集像素数: {union_matrix.sum()}")# 3. 计算IoU
intersection_count = intersection_matrix.sum()
union_count = union_matrix.sum()
iou_manual = intersection_count / union_count
print(f"\n手动计算IoU: {intersection_count}/{union_count} = {iou_manual:.4f}")

没什么好介绍的，概念很直接，以图像识别为例的话，其实就是多维数值的分析。

其他一些需要注意的点：

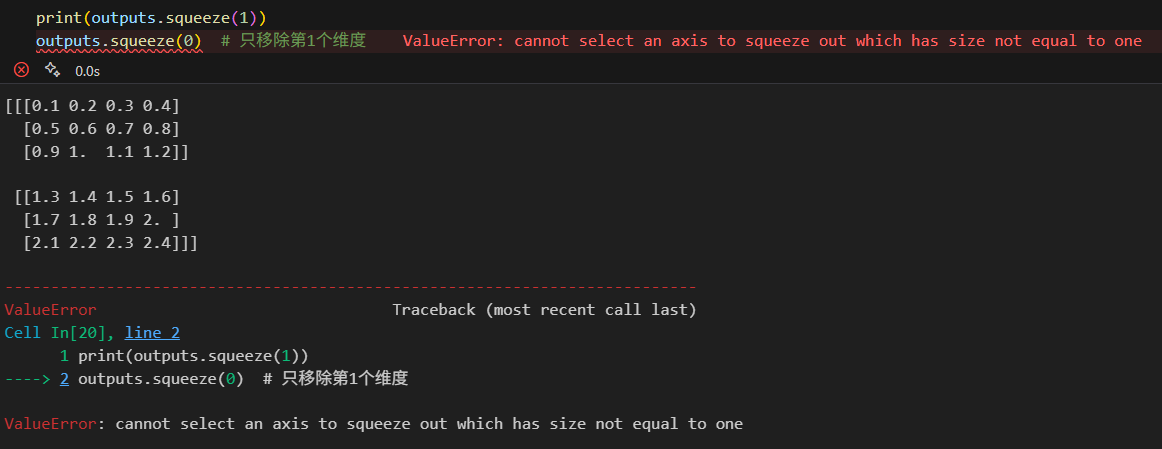
squeeze就是自动移除大小只有1的维度，当然也可以自己指定如果自己知道数组的哪个维度大小只有1。

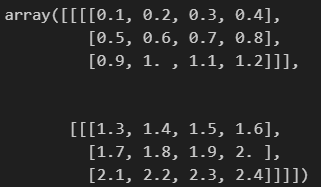
import numpy as np# 创建一个形状为 (2, 1, 3, 4) 的数组
outputs = np.array([[[[0.1, 0.2, 0.3, 0.4],[0.5, 0.6, 0.7, 0.8],[0.9, 1.0, 1.1, 1.2]]],[[[1.3, 1.4, 1.5, 1.6],[1.7, 1.8, 1.9, 2.0],[2.1, 2.2, 2.3, 2.4]]]
])
outputs

# 输出形状
print(f"形状：{outputs.shape}")
# (2, 1, 3, 4)，简单理解为2块1组3行4列，逐层去掉每个维度的括号# 输出第1块
print(f"第1块：{outputs[0]}")# 在第1块基础上输出第1组
print(f"第1块第1组：{outputs[0,0]}")
# 这个是直接使用2D索引，也可以分步outputs[0][0]# 在第1块第1组基础上输出第1行
print(f"第1块第1组第1行：{outputs[0,0,0]}")
# 同理也可以直接使用outputs[0][0][0]# 在第1块第1组第1行基础上输出第1列
print(f"第1块第1组第1行第1列：{outputs[0,0,0,0]}")

# 移除长度为1的维度数据print(f"原始的维度：{outputs.ndim}") # 4个维度# 移除长度为1的维度数据
print(outputs.squeeze())
print(f"现在的维度：{outputs.squeeze().ndim}")

（2）如果是在pytorch中：

import torchSMOOTH = 1e-6def IoU_pytorch(outputs: torch.Tensor, labels: torch.Tensor):# 如果是传递相同shape的tensor，那就不一定需要squeeze# 如果是传递UNet或者是其他网络中的输出，很大可能是BATCH x 1 x H x W的shapeoutputs = outputs.squeeze(1)  # BATCH x 1 x H x W => BATCH x H x Wintersection = (outputs & labels).float().sum((1, 2))  # 如果Truth=0或Prediction=0，结果为0union = (outputs | labels).float().sum((1, 2))         # 同0则0iou = (intersection + SMOOTH) / (union + SMOOTH)  # ⚠️⚠️⚠️同上操作，可以止步于此thresholded = torch.clamp(20 * (iou - 0.7), 0, 10).ceil() / 10  return thresholded  # 或者thresholded.mean()，计算整个批次的平均值