当前位置：首页 > news >正文

基于混合注意力网络和深度信念网络的鲁棒视频水印技术基础理论深度解析

news 2025/8/22 6:24:51

1. 引言

随着数字媒体技术的迅猛发展和互联网的普及，视频内容的创作、传播和分享变得前所未有的便捷。然而，这种便利性也带来了严重的版权保护挑战。数字视频的易复制性使得盗版和非法传播成为困扰内容创作者和版权所有者的重大问题。传统的加密技术虽然能够在一定程度上保护数字内容，但一旦内容被解密，就失去了进一步的保护能力。在这种背景下，数字水印技术作为一种新兴的版权保护手段应运而生，它能够将版权信息直接嵌入到数字媒体内容中，实现对数字内容的持久性保护。

数字水印技术的核心思想是在不影响原始内容感知质量的前提下，将特定的标识信息（水印）隐藏在数字媒体中。这些水印信息在正常的观看或使用过程中是不可见或不可感知的，但可以通过特定的算法和密钥提取出来，从而实现对数字内容的版权认证、完整性验证和来源追溯。与传统的版权保护方法相比，数字水印技术具有隐蔽性强、鲁棒性好、容量大等优势，已经成为数字版权保护领域的重要技术手段。

视频水印作为数字水印技术的重要分支，面临着比图像水印更为复杂的技术挑战。视频数据不仅具有空间维度的特征，还包含时间维度的信息，这使得视频水印需要在空域、频域和时域等多个维度上进行考虑。同时，视频在传输和存储过程中可能遭受各种有意或无意的攻击，如压缩、噪声添加、几何变换、帧操作等，这要求视频水印算法必须具备足够的鲁棒性来抵抗这些攻击。

近年来，深度学习技术的快速发展为数字水印领域带来了新的机遇和挑战。基于深度学习的水印方法能够自动学习数据的深层特征表示，实现更加智能和自适应的水印嵌入和提取策略。特别是注意力机制的引入，使得水印算法能够动态地关注视频内容中最重要的区域，从而在保证不可感知性的同时提高鲁棒性。

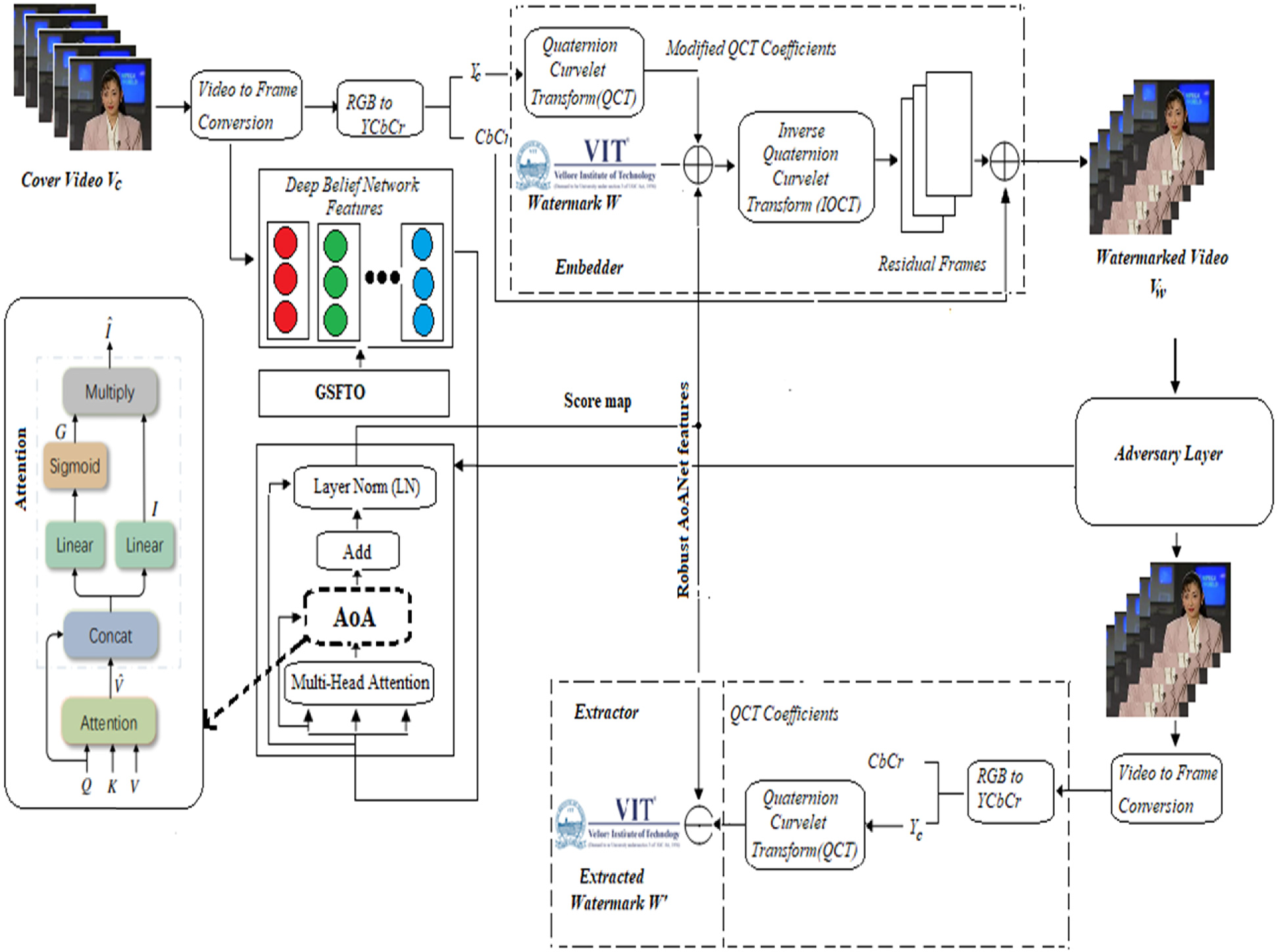
论文《DeepSecure watermarking: Hybrid Attention on Attention Net and Deep Belief Net based robust video authentication using Quaternion Curvelet Transform domain》提出了一种创新的视频水印方法，该方法巧妙地融合了多种先进技术，包括注意力机制（Attention Mechanism）、深度信念网络（Deep Belief Network）、四元数曲波变换（Quaternion Curvelet Transform）以及黄金分割斐波那契树优化算法（Golden Section Fibonacci Tree Optimization）。这种多技术融合的方法在视频水印的不可感知性和鲁棒性之间实现了良好的平衡，为视频版权保护提供了新的技术路径。

2. 数字水印技术基础理论

2.1 数字水印的基本概念与分类

数字水印技术起源于物理世界中的纸质水印概念，但其内涵和外延都得到了极大的扩展。从技术角度来看，数字水印是一种信息隐藏技术，它将特定的数字信号（水印）嵌入到数字媒体载体中，使得水印信息与载体内容紧密结合，难以被分离或篡改。这种嵌入过程需要满足两个基本要求：一是不可感知性（Imperceptibility），即水印的嵌入不应该明显影响载体的感知质量；二是鲁棒性（Robustness），即水印信息应该能够抵抗各种可能的攻击和处理操作。

根据水印嵌入的域空间不同，数字水印技术可以分为空域水印和变换域水印两大类。空域水印直接在像素层面进行操作，通过修改图像或视频帧的像素值来嵌入水印信息。最典型的空域水印方法是最低有效位（Least Significant Bit, LSB）方法，它将水印信息替换载体图像的最低有效位。LSB方法的优点是实现简单、嵌入容量大，但缺点是鲁棒性较差，容易受到各种信号处理操作的影响。另一种常见的空域方法是叠加法，它将水印信号与载体信号直接相加，数学表达式为：

$I_w(x,y) = I(x,y) + \alpha \cdot W(x,y)$

其中 $I(x,y)$ 表示原始载体图像， $W(x,y)$ 表示水印信号， $\alpha$ 表示嵌入强度因子， $I_w(x,y)$ 表示嵌入水印后的图像。

变换域水印则是在频域中进行水印嵌入，它首先将载体信号通过某种数学变换转换到频域，然后在变换系数中嵌入水印信息，最后通过逆变换得到嵌入水印的载体信号。常用的变换包括离散余弦变换（DCT）、离散小波变换（DWT）、离散傅里叶变换（DFT）等。变换域水印的主要优势在于其良好的鲁棒性，因为频域系数通常对常见的信号处理操作（如压缩、滤波等）具有更强的抗干扰能力。例如，在DCT域中的水印嵌入可以表示为：

$C_w(u,v) = C(u,v) + \alpha \cdot W(u,v)$

其中 $C(u,v)$ 表示原始DCT系数， $W(u,v)$ 表示水印信号在DCT域的表示， $C_w(u,v)$ 表示嵌入水印后的DCT系数。

2.2 视频水印的特殊挑战

与静态图像相比，视频水印面临着更多的技术挑战。首先，视频具有时间维度，这使得水印算法需要考虑帧间的相关性和时间一致性。视频中相邻帧之间往往存在很强的相关性，这种相关性既可以被利用来提高水印的鲁棒性，也可能成为攻击者利用的弱点。其次，视频数据量庞大，对算法的计算效率提出了更高的要求。一个典型的高清视频文件可能包含数十万帧图像，如果对每一帧都进行复杂的水印处理，将会带来巨大的计算开销。

视频在传输和存储过程中还可能遭受各种特有的攻击，包括时域攻击和空域攻击。时域攻击主要针对视频的时间特性，如帧丢弃（Frame Dropping）、帧重排（Frame Reordering）、帧插入（Frame Insertion）等。这些攻击会破坏视频的时间结构，可能导致基于时间相关性的水印信息丢失。空域攻击则包括传统的图像处理攻击，如噪声添加、滤波、几何变换等，以及视频特有的压缩攻击。视频压缩是视频处理中最常见的操作，不同的压缩标准（如H.264、H.265等）采用不同的压缩算法，这些算法可能会显著影响嵌入的水印信息。

为了应对这些挑战，视频水印算法通常采用关键帧（Key Frame）选择策略，即只在视频的关键帧中嵌入水印信息。关键帧的选择需要考虑多个因素，包括帧的重要性、视觉显著性、运动信息等。数学上，关键帧的选择可以建模为一个优化问题：

$\arg\max_{F \subset {f_1, f_2, ..., f_N}} \sum_{f_i \in F} \text{Importance}(f_i)$

其中 ${f_1, f_2, ..., f_N}$ 表示视频中的所有帧，F表示选择的关键帧集合， $\text{Importance}(f_i)$ 表示第 $i$ 帧的重要性度量。

2.3 水印系统的性能评价指标

数字水印系统的性能通常通过多个指标来评价，这些指标反映了水印算法在不可感知性、鲁棒性、安全性等方面的表现。不可感知性是衡量水印嵌入对载体质量影响程度的指标，常用的客观评价指标包括峰值信噪比（Peak Signal-to-Noise Ratio, PSNR）和结构相似性指数（Structural Similarity Index, SSIM）。PSNR的计算公式为：

$\text{PSNR} = 10 \log_{10} \frac{\text{MAX}^2}{\text{MSE}}$

其中MAX表示图像可能的最大像素值，MSE表示均方误差：

$\text{MSE} = \frac{1}{MN} \sum_{i=0}^{M-1} \sum_{j=0}^{N-1} [I(i,j) - I_w(i,j)]^2$

SSIM指标考虑了人眼视觉系统的特性，通过比较亮度、对比度和结构信息来评价图像质量：

$\text{SSIM}(x,y) = \frac{(2\mu_x\mu_y + c_1)(2\sigma_{xy} + c_2)}{(\mu_x^2 + \mu_y^2 + c_1)(\sigma_x^2 + \sigma_y^2 + c_2)}$

其中 $\mu_x,\mu_y$ 分别表示图像x和y的均值， $\sigma_x^2,\sigma_y^2$ 分别表示方差， $\sigma_{xy}$ 表示协方差， $c_1,c_2$ 为常数。

鲁棒性评价主要关注水印在各种攻击下的生存能力，常用指标包括归一化相关系数（Normalized Correlation Coefficient, NCC）和误码率（Bit Error Rate, BER）。NCC用于衡量提取水印与原始水印之间的相似度：

$\text{NCC} = \frac{\sum_{i=1}^{N} W_i \cdot W'i}{\sqrt{\sum{i=1}^{N} W_i^2} \sqrt{\sum_{i=1}^{N} W'^2_i}}$

其中 $W_i$ 表示原始水印的第i个元素， $W'_i$ 表示提取水印的第i个元素。BER则计算错误提取的比特数占总比特数的比例：

3. 注意力机制的基础原理

3.1 注意力机制的生物学启发与数学基础

注意力机制源于对人类认知过程的模拟，特别是人类视觉注意力系统的工作原理。在日常生活中，人类面对复杂的视觉场景时，并不会同时关注所有的细节，而是会选择性地将注意力集中在最重要或最相关的信息上。这种选择性注意的能力使得人类能够在有限的认知资源下高效地处理大量信息。心理学研究表明，人类的注意力机制包括自下而上（bottom-up）和自上而下（top-down）两种模式。自下而上的注意力由刺激的显著性驱动，而自上而下的注意力则由任务目标和先验知识引导。

在深度学习中，注意力机制的数学基础可以追溯到信息论和概率论。从信息论的角度来看，注意力机制可以理解为一种信息选择和过滤机制，它通过分配不同的权重来突出重要信息，抑制不相关信息。数学上，注意力机制可以表示为一个加权平均的过程：

$\text{Attention}(Q, K, V) = \sum_{i=1}^{n} \alpha_i v_i$

其中Q表示查询（Query），K表示键（Key），V表示值（Value）， $\alpha_i$ 表示注意力权重， $v_i$ 表示第i个值向量。注意力权重 $\alpha_i$ 的计算通常涉及查询和键之间的相似度计算：

$\alpha_i = \frac{\exp(f(q, k_i))}{\sum_{j=1}^{n} \exp(f(q, k_j))}$

其中 $f(q, k_i)$ 表示查询q与第i个键 $k_i$ 之间的相似度函数，常用的相似度函数包括点积、加性注意力、多层感知机等。

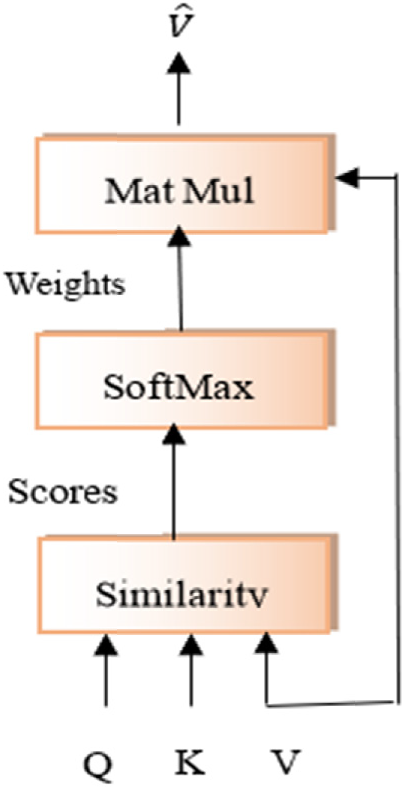
3.2 Scaled Dot-Product Attention的数学原理

Scaled Dot-Product Attention是最常用的注意力计算方法，它使用向量点积来计算查询和键之间的相似度。点积操作的几何意义是计算两个向量之间的夹角余弦，当两个向量方向相似时，点积值较大，表示较高的相关性。Scaled Dot-Product Attention的完整计算公式为：

$\text{Attention}(Q, K, V) = \text{softmax}\left(\frac{QK^T}{\sqrt{d_k}}\right)V$

其中 $d_k$ 表示键向量的维度，除以 $\sqrt{d_k}$ 的目的是进行缩放，防止点积结果过大导致softmax函数进入饱和区域。这种缩放的必要性可以从统计学角度来理解：假设Q和K的元素是独立的随机变量，均值为0，方差为1，那么它们的点积的方差为 $d_k$ 。通过除以 $\sqrt{d_k}$ ，可以使得缩放后的点积具有单位方差，从而稳定训练过程。

softmax函数将注意力分数转换为概率分布：

$\text{softmax}(x_i) = \frac{\exp(x_i)}{\sum_{j=1}^{n} \exp(x_j)}$

这确保了所有注意力权重的和为1，符合概率分布的定义。从信息论的角度来看，softmax函数实现了一种"软选择"机制，相比于硬性的最大值选择，软选择能够保留更多的信息，有利于梯度的反向传播。

3.3 多头注意力机制的并行处理能力

多头注意力（Multi-Head Attention）是对单头注意力的扩展，它并行计算多个注意力头，每个头关注输入的不同方面。这种设计的理论基础来自于集成学习的思想，多个弱学习器的组合往往能够获得比单个强学习器更好的性能。在注意力机制中，不同的头可以学习到不同类型的依赖关系，如短距离依赖、长距离依赖、句法依赖、语义依赖等。

多头注意力的数学表达式为：

$\text{MultiHead}(Q, K, V) = \text{Concat}(\text{head}_1, ..., \text{head}_h)W^O$

其中每个注意力头的计算为：

$\text{head}_i = \text{Attention}(QW_i^Q, KW_i^K, VW_i^V)$

这里 $W_i^Q \in \mathbb{R}^{d_{model} \times d_k},W_i^K \in \mathbb{R}^{d_{model} \times d_k},W_i^V \in \mathbb{R}^{d_{model} \times d_v}$ 是可学习的投影矩阵， $W^O \in \mathbb{R}^{hd_v \times d_{model}}$ 是输出投影矩阵。通过这些投影矩阵，不同的头可以学习到输入在不同子空间中的表示。

多头注意力的一个重要优势是计算的并行性。由于不同头之间的计算相互独立，可以在现代GPU架构上高效地并行执行。这种并行性不仅提高了计算效率，还增强了模型的表达能力。理论分析表明，多头注意力能够捕获输入序列中的多种模式和关系，其表达能力随着头数的增加而增强，但存在边际递减效应。

3.4 自注意力机制的长距离依赖建模

自注意力（Self-Attention）是注意力机制的一个特殊情况，其中查询、键和值都来自同一个输入序列。自注意力的核心优势在于能够直接建模序列中任意两个位置之间的依赖关系，而不受距离限制。这与传统的循环神经网络（RNN）形成鲜明对比，RNN需要逐步传递信息，对于长距离依赖的建模能力有限。

自注意力机制的计算复杂度为 $O(n^2 d)$ ，其中n是序列长度，d是特征维度。虽然这种二次复杂度在长序列上可能成为瓶颈，但对于中等长度的序列，自注意力的并行性和建模能力使其成为理想的选择。更重要的是，自注意力的权重矩阵提供了序列中不同位置之间关系的直观可视化，这对于理解模型的行为具有重要价值。

在数学上，自注意力可以看作是输入序列的一种自适应重新组合。对于输入序列 $X = [x_1, x_2, ..., x_n]$ ，自注意力的输出为：

$Y = \text{SelfAttention}(X) = \text{softmax}\left(\frac{XX^T}{\sqrt{d}}\right)X$

这个公式展现了自注意力的本质：首先计算序列中每对元素的相似度（ $XX^T$ ），然后将这些相似度作为权重，对原始序列进行加权组合。这种机制使得每个输出位置都能够"看到"输入序列的全局信息，从而实现了全局上下文的有效建模。

4. Attention on Attention网络的深度解析

4.1 传统注意力机制的局限性分析

传统的注意力机制虽然在许多任务中取得了显著的成功，但仍然存在一些固有的局限性。其中最主要的问题是注意力机制的"盲目性"，即无论输入的相关性如何，注意力机制总是会产生一个归一化的权重分布。这意味着即使输入中没有相关信息，注意力机制仍然会强制分配权重，可能导致不相关信息被错误地纳入最终表示中。这种现象在信息检索和问答系统中尤为明显，当查询与所有候选项都不相关时，传统注意力机制仍然会选择"最不相关"的项作为答案。

从数学角度分析，传统注意力机制的输出可以表示为：

$c = \sum_{i=1}^{n} \alpha_i v_i, \quad \sum_{i=1}^{n} \alpha_i = 1$

由于softmax函数的归一化特性，权重 $\alpha_i$ 总是非负且和为1。这意味着输出c始终是输入值 $v_i$ 的凸组合，无法表示"无相关信息"的情况。在实际应用中，这可能导致模型学习到虚假的相关性，特别是在训练数据存在噪声或标注错误的情况下。

另一个重要的局限性是传统注意力机制缺乏对注意力质量的评估能力。在人类认知中，注意力不仅涉及"关注什么"，还包括"关注程度"的控制。例如，当面对模糊或不确定的刺激时，人类会调节注意力的强度，而不是盲目地分配最大注意力。传统的注意力机制缺乏这种自适应调节能力，可能在处理低质量或不确定输入时产生过拟合现象。

4.2 AoA网络的设计理念与创新点

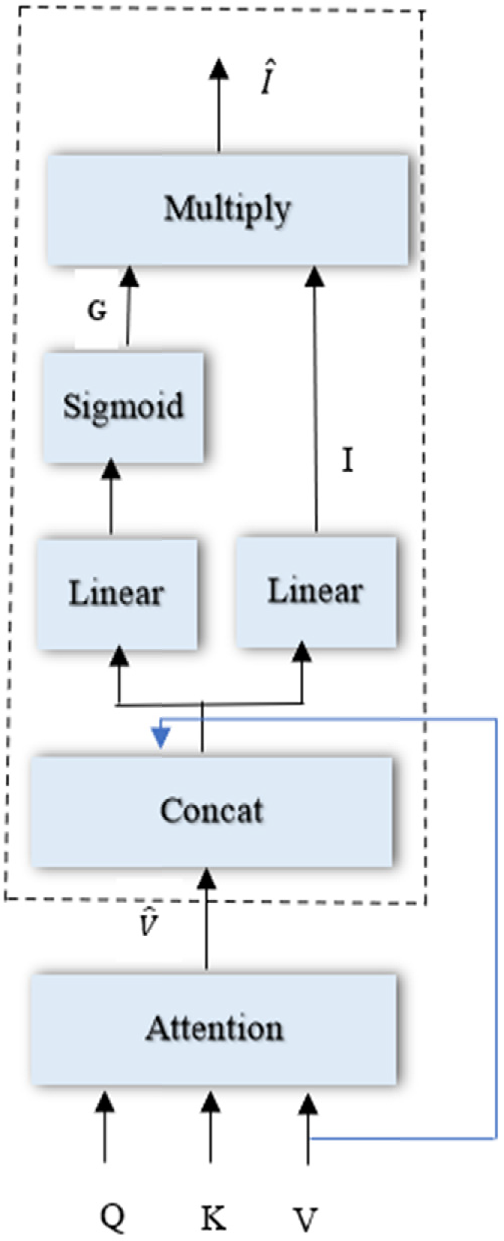
Attention on Attention（AoA）网络的核心思想是在传统注意力机制的基础上增加一个"注意力门控"机制，用于控制注意力信息的流动。这种设计受到了门控机制在循环神经网络中成功应用的启发，如LSTM和GRU中的遗忘门、输入门等。AoA网络通过引入注意力门控，使得模型能够自适应地决定是否以及在多大程度上使用注意力信息。

AoA网络的数学模型包含两个关键组件：信息向量（Information Vector）和注意力门控（Attention Gate）。信息向量$i$通过线性变换生成，包含了当前上下文的丰富信息：

$i = W_q^i Q + W_v^i \hat{V} + b^i$

其中Q表示查询， $\hat{V}$ 表示传统注意力机制的输出， $W_q^i,W_v^i$ 是可学习的权重矩阵， $b^i$ 是偏置向量。

注意力门控g通过sigmoid激活函数生成，其值在0到1之间，控制信息流的强度：

$g = \sigma(W_q^g Q + W_v^g \hat{V} + b^g)$

最终的AoA输出通过元素级乘法得到：

$\hat{i} = g \odot i$

这种设计的巧妙之处在于，当门控值接近0时，模型会抑制注意力信息的传递，有效地表达"无相关信息"的语义；当门控值接近1时，模型会充分利用注意力信息。这种自适应控制机制使得AoA网络能够根据输入的质量和相关性动态调整注意力的强度。

4.3 AoA网络的信息论解释

从信息论的角度来看，AoA网络实现了一种更加智能的信息选择机制。传统注意力机制可以看作是一种有损压缩过程，它将输入序列压缩为固定长度的表示向量。然而，这种压缩是"强制性"的，即使输入信息质量很低，也会产生一个表示向量。AoA网络通过引入门控机制，实现了"自适应压缩"，当输入信息质量不足时，可以选择产生近似零向量的输出。

这种机制可以用条件信息论来解释。设Y表示AoA网络的输出，X表示输入，R表示相关性变量，那么AoA网络的目标可以表示为：

$\max I(Y; T|R) - \lambda I(Y; X|R=0)$

其中T表示目标任务， $I(\cdot; \cdot|\cdot)$ 表示条件互信息， $\lambda$ 是正则化参数。第一项鼓励输出与目标任务的相关性，第二项惩罚在无相关信息时的输出复杂度。这种目标函数确保了AoA网络在有相关信息时最大化信息传递，在无相关信息时最小化噪声传播。

4.4 AoA网络在视频水印中的应用机制

在视频水印的应用场景中，AoA网络被用于生成分数图（Score Map），指导水印的嵌入位置选择。视频帧的不同区域具有不同的纹理复杂度、视觉显著性和鲁棒性特征，AoA网络通过分析这些特征，生成一个分数图来指示每个像素位置的嵌入适宜性。

具体而言，AoA网络接收从深度信念网络提取的视频帧特征作为输入，通过多头注意力机制分析特征之间的相关性，然后通过门控机制生成最终的分数图。这个过程可以数学化表示为：

$\text{ScoreMap}i = \text{AoA}(f{\text{att}}, Q_i, K_i, V_i)$

其中 $Q_i,K_i,V_i$ 分别表示第i个视频帧的查询、键、值表示， $f_{\text{att}}$ 表示注意力函数。

生成的分数图具有重要的语义含义：高分数区域通常对应于纹理丰富、视觉不敏感且具有较强鲁棒性的区域，这些区域适合嵌入水印信息；低分数区域则对应于平滑、视觉敏感或容易受攻击影响的区域，应该避免在这些区域嵌入水印。这种自适应的位置选择策略显著提高了水印系统的整体性能，实现了不可感知性和鲁棒性的良好平衡。

5. 深度信念网络的理论基础

5.1 概率图模型与生成式建模

深度信念网络（Deep Belief Network, DBN）是一种基于概率图模型的深度生成模型，由Geoffrey Hinton在2006年提出。DBN的理论基础建立在概率图模型和无监督学习的交汇点上，它通过学习数据的概率分布来实现特征提取和数据生成的双重功能。与传统的判别式模型不同，生成式模型试图学习数据的联合概率分布P(X, Y)，其中X表示输入数据，Y表示标签。这种建模方式使得生成式模型不仅能够进行分类预测，还能够生成新的数据样本。

DBN的概率建模基础可以追溯到统计物理学中的玻尔兹曼分布。在这种框架下，系统的状态由一个能量函数 $E(\mathbf{v}, \mathbf{h})$ 决定，其中 $\mathbf{v}$ 表示可见变量， $\mathbf{h}$ 表示隐变量。系统的概率分布遵循玻尔兹曼分布：

$P(\mathbf{v}, \mathbf{h}) = \frac{1}{Z} \exp(-E(\mathbf{v}, \mathbf{h}))$

其中Z是配分函数（Partition Function），用于归一化概率分布：

$Z = \sum_{\mathbf{v}, \mathbf{h}} \exp(-E(\mathbf{v}, \mathbf{h}))$

这种概率建模方式的优势在于能够捕获变量之间的复杂依赖关系，特别是高阶相关性。在传统的线性模型中，变量之间的关系通常假设为线性或简单的非线性关系，而基于能量的模型能够表示任意复杂的依赖结构。

5.2 受限玻尔兹曼机的数学原理

受限玻尔兹曼机（Restricted Boltzmann Machine, RBM）是DBN的基本构建单元。RBM是一种特殊的玻尔兹曼机，其"受限"特性体现在网络结构的约束上：可见层内部没有连接，隐藏层内部也没有连接，只有可见层和隐藏层之间存在全连接。这种结构约束大大简化了模型的训练过程，使得条件概率的计算变得可行。

RBM的能量函数定义为：

$E(\mathbf{v}, \mathbf{h}) = -\mathbf{v}^T \mathbf{W} \mathbf{h} - \mathbf{a}^T \mathbf{v} - \mathbf{b}^T \mathbf{h}$

其中$\mathbf{W}$是连接权重矩阵，$\mathbf{a}$和$\mathbf{b}$分别是可见层和隐藏层的偏置向量。基于这个能量函数，可以推导出条件概率分布：

$P(h_j = 1|\mathbf{v}) = \sigma\left(\sum_i W_{ij} v_i + b_j\right)$$ $$P(v_i = 1|\mathbf{h}) = \sigma\left(\sum_j W_{ij} h_j + a_i\right)$

其中 $\sigma(x) = \frac{1}{1 + \exp(-x)}$ 是sigmoid激活函数。

这些条件概率公式揭示了RBM的重要特性：给定可见层的状态，隐藏层单元的激活是相互独立的；反之亦然。这种条件独立性是RBM可训练性的关键，它使得可以通过Gibbs采样高效地从模型分布中采样。

RBM的训练目标是最大化观测数据的对数似然：

$\mathcal{L} = \sum_{n=1}^{N} \log P(\mathbf{v}^{(n)})$

其中边际概率 $P(\mathbf{v})$ 通过对隐变量求和得到：

$P(\mathbf{v}) = \sum_{\mathbf{h}} P(\mathbf{v}, \mathbf{h}) = \sum_{\mathbf{h}} \frac{1}{Z} \exp(-E(\mathbf{v}, \mathbf{h}))$

5.3 对比散度算法的理论基础

RBM的直接最大似然训练面临着配分函数难以计算的问题，因为需要对所有可能的状态组合求和。为了解决这个问题，Hinton提出了对比散度（Contrastive Divergence, CD）算法，这是一种近似的梯度估计方法。

对比散度算法的核心思想是用短链Gibbs采样来近似模型分布下的期望。标准的梯度计算需要计算数据分布和模型分布下的期望差：

$\frac{\partial \mathcal{L}}{\partial \theta} = \mathbb{E}{\text{data}}[\frac{\partial E}{\partial \theta}] - \mathbb{E}{\text{model}}[\frac{\partial E}{\partial \theta}]$

其中第一项可以直接从训练数据计算，第二项需要从模型分布采样。对比散度算法用$k$步Gibbs采样来近似模型分布下的期望：

从训练样本 $\mathbf{v}^{(0)}$ 开始
计算 $P(\mathbf{h}^{(0)}|\mathbf{v}^{(0)})$ 并采样 $\mathbf{h}^{(0)}$
计算 $P(\mathbf{v}^{(1)}|\mathbf{h}^{(0)})$ 并采样 $\mathbf{v}^{(1)}$
重复k次得到 $\mathbf{v}^{(k)}$

对比散度的梯度估计为：

$\frac{\partial \mathcal{L}{\text{CD}}}{\partial \theta} = \mathbb{E}{\text{data}}[\frac{\partial E}{\partial \theta}] - \mathbb{E}_{\mathbf{v}^{(k)}}[\frac{\partial E}{\partial \theta}]$

理论分析表明，当 $k \to \infty$ 时，CD算法收敛到真实的最大似然梯度。在实践中，即使k=1（CD-1），算法也能获得良好的性能。这种近似的理论基础在于Gibbs采样的快速混合性质：在大多数实际数据分布下，短链采样已经能够捕获模型分布的主要特征。

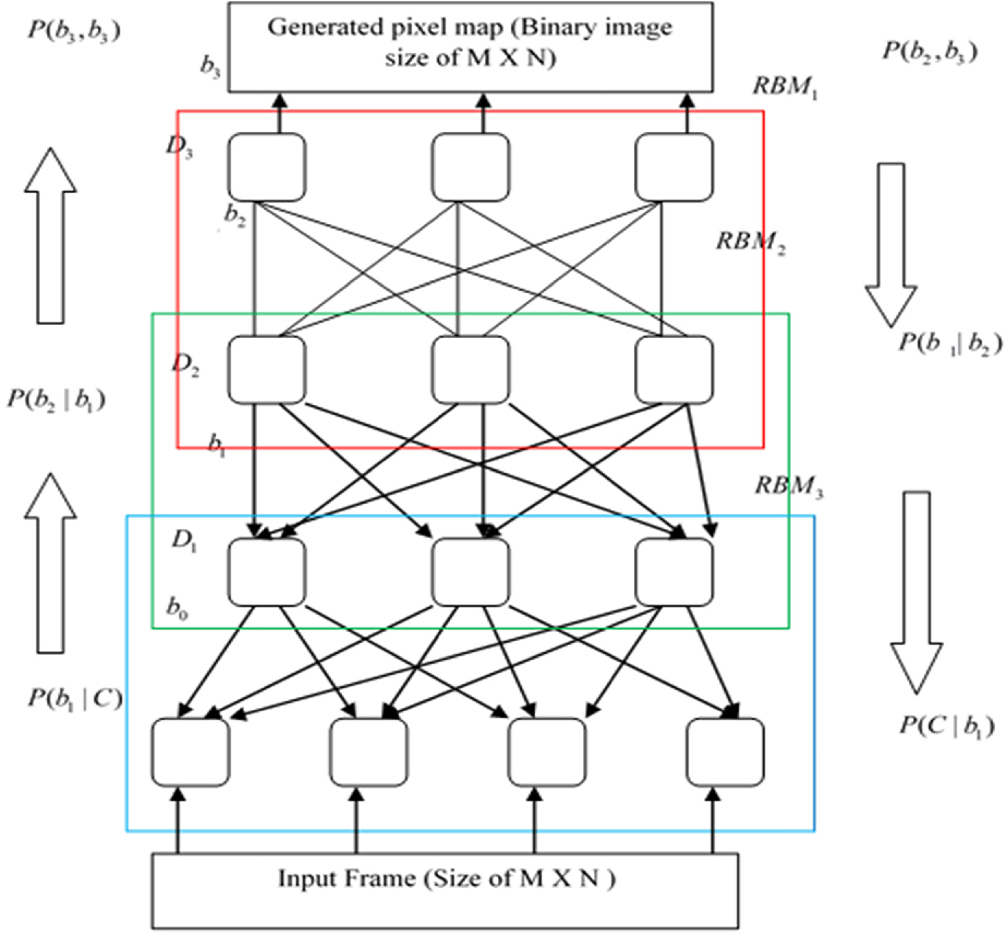
5.4 DBN的逐层贪心训练策略

DBN通过逐层贪心训练策略解决了深层网络的训练难题。这种策略的理论依据来自于复合函数的近似理论和信息瓶颈原理。每一层RBM可以看作是对输入数据的一种信息压缩和特征提取，而多层的堆叠则实现了层次化的特征学习。

DBN的训练过程可以分为两个阶段：无监督预训练和有监督微调。在预训练阶段，从底层开始，逐层训练每个RBM：

训练第一层RBM： ${W^{(1)}, \mathbf{a}^{(1)}, \mathbf{b}^{(1)}} = \arg\max_{\theta} \sum_n \log P(\mathbf{v}_n; \theta)$
固定第一层参数，用 $P(\mathbf{h}^{(1)}|\mathbf{v})$ 的期望作为第二层的输入
训练第二层RBM： ${W^{(2)}, \mathbf{b}^{(1)}, \mathbf{b}^{(2)}} = \arg\max_{\theta} \sum_n \log P(\mathbf{h}_n^{(1)}; \theta)$
重复直到所有层训练完成

这种逐层训练策略的理论优势在于每一层的训练都有明确的目标函数，避免了深层网络训练中的梯度消失和局部最优问题。更重要的是，每一层都学习到了前一层表示的更抽象的特征，实现了从低级特征到高级特征的层次化学习。

数学上，DBN的完整概率模型可以表示为：

$P(\mathbf{v}, \mathbf{h}^{(1)}, ..., \mathbf{h}^{(L)}) = P(\mathbf{v}|\mathbf{h}^{(1)}) \prod_{l=1}^{L-1} P(\mathbf{h}^{(l)}|\mathbf{h}^{(l+1)}) P(\mathbf{h}^{(L-1)}, \mathbf{h}^{(L)})$

其中底层是有向的信念网络，顶层是无向的RBM。这种混合的图结构既保留了生成模型的优势，又具有了判别模型的表达能力。

6. 四元数曲波变换的数学原理

6.1 四元数代数的基础理论

四元数（Quaternion）是由爱尔兰数学家Hamilton在1843年发明的一种扩展的数系统，它是复数在高维空间的推广。四元数在计算机图形学、机器人学和信号处理等领域有着广泛的应用，特别是在表示三维旋转和处理彩色图像时展现出独特的优势。一个四元数可以表示为：

$q = q_0 + q_1 i + q_2 j + q_3 k$

其中 $q_0, q_1, q_2, q_3 \in \mathbb{R},i, j, k$ 是四元数的基本单位，满足以下乘法规则：

$i^2 = j^2 = k^2 = ijk = -1$$ $$ij = k, \quad jk = i, \quad ki = j$$ $$ji = -k, \quad kj = -i, \quad ik = -j$

这些乘法规则定义了四元数的非交换代数结构，这种非交换性使得四元数能够表示三维空间中的旋转操作。

在信号处理中，四元数的一个重要应用是表示彩色图像。传统的彩色图像处理方法通常将RGB三个通道分别处理，忽略了通道之间的相关性。而四元数表示法可以将彩色图像编码为一个四元数信号：

$f(x, y) = f_R(x, y) i + f_G(x, y) j + f_B(x, y) k$

其中 $f_R, f_G, f_B$ 分别表示红、绿、蓝三个颜色通道。这种表示方法的优势在于能够同时处理三个颜色通道，保持通道间的相关性，从而获得更好的处理效果。

四元数的模长定义为：

$|q| = \sqrt{q_0^2 + q_1^2 + q_2^2 + q_3^2}$

四元数的共轭定义为：

$\bar{q} = q_0 - q_1 i - q_2 j - q_3 k$

四元数的逆定义为：

$q^{-1} = \frac{\bar{q}}{|q|^2}$

6.2 四元数傅里叶变换的理论基础

四元数傅里叶变换（Quaternion Fourier Transform, QFT）是傅里叶变换在四元数域的推广，它能够同时分析信号在多个维度上的频域特性。二维QFT的定义为：

$\mathcal{F}q[f](u, v) = \int{-\infty}^{\infty} \int_{-\infty}^{\infty} f(x, y) e^{-\mu 2\pi(ux + vy)} dx dy$

其中 $\mu$ 是一个单位纯四元数，通常选择为 $\mu = \frac{i + j + k}{\sqrt{3}}$ 。这个选择确保了变换的对称性和旋转不变性。

QFT的一个重要特性是它能够将信号分解为不同方向和频率的分量。与传统的复数傅里叶变换相比，QFT提供了更丰富的频域表示，能够更好地分析彩色图像和多通道信号的特性。QFT的逆变换定义为：

$f(x, y) = \int_{-\infty}^{\infty} \int_{-\infty}^{\infty} \mathcal{F}_q[f](u, v) e^{\mu 2\pi(ux + vy)} du dv$

QFT具有线性性、平移性、旋转协变性等重要性质。特别地，QFT的旋转协变性表明，当输入信号发生旋转时，其QFT也会发生相应的旋转，这种性质在处理几何变换时非常有用。

6.3 曲波变换的多尺度几何分析

曲波变换（Curvelet Transform）是一种新兴的多尺度几何分析工具，由Candès和Donoho在21世纪初提出。与传统的小波变换相比，曲波变换在处理具有方向性特征的信号时具有显著优势，特别是在图像中的边缘和线性特征分析方面。

曲波变换的基本思想是构造一族具有方向选择性的基函数，这些基函数在不同尺度上具有不同的长宽比。在粗尺度上，曲波基函数接近于各向同性的；在细尺度上，曲波基函数变得高度各向异性，呈现出细长的形状。这种设计使得曲波能够稀疏地表示具有线性和曲线特征的信号。

连续曲波的定义基于极坐标系。在频域中，曲波的支撑集由尺度参数a和角度参数 $\theta$ 确定：

$\text{supp}(\hat{\psi}_{a,\theta}) \subset {(\rho, \phi) : \rho \sim 2^{-j}, |\phi - \theta| \lesssim 2^{-j/2}}$

其中j是尺度指标， $\rho$ 和 $\phi$ 分别表示极径和极角。这个支撑集的形状类似于楔形，其宽度随着尺度的减小而减小，体现了曲波的方向选择性。

离散曲波变换通过在频域中的楔形分割来实现。具体步骤包括：

对输入信号进行2D FFT
在频域中应用角度和径向窗函数
对每个楔形区域进行逆FFT
应用适当的重采样和包装操作

曲波变换的一个重要理论结果是其在表示分片光滑图像时的最优稀疏性。对于包含$C^2$曲线的分片$C^2$图像，曲波变换能够实现接近最优的非线性逼近误差。

6.4 四元数曲波变换的构造与性质

四元数曲波变换（Quaternion Curvelet Transform, QCT）是曲波变换在四元数域的推广，它结合了四元数代数的优势和曲波变换的几何分析能力。QCT的构造基于四元数傅里叶变换和曲波分析的结合。

QCT的实现过程可以描述如下：

将输入的彩色图像表示为四元数信号： $f_q(x, y) = f_R(x, y) i + f_G(x, y) j + f_B(x, y) k$
计算四元数傅里叶变换： $\hat{f}_q(u, v) = \mathcal{F}_q[f_q](u, v)$
在四元数频域中应用曲波分析： $C_{j,l,k} = \langle \hat{f}q, \hat{\psi}{j,l,k} \rangle$

其中j, l, k分别表示尺度、方向和位置参数， $\hat{\psi}_{j,l,k}$ 是四元数曲波基函数。

QCT具有以下重要性质：

完美重构性：存在对偶基函数使得原始信号可以完美重构： $f_q = \sum_{j,l,k} C_{j,l,k} \psi_{j,l,k}$

旋转协变性：当输入信号发生旋转时，QCT系数也会发生相应的变化，保持几何结构的一致性。

颜色不变性：QCT能够捕获图像的几何结构信息，对颜色空间的线性变换具有一定的鲁棒性。

稀疏表示：对于具有方向性特征的彩色图像，QCT能够提供稀疏的表示，大部分能量集中在少数几个重要系数上。

在水印应用中，QCT的优势主要体现在：

多通道处理：能够同时处理RGB三个颜色通道，保持通道间的相关性
方向选择性：能够精确定位图像中的边缘和纹理方向
多尺度分析：在不同尺度上提供不同的频率分辨率
几何不变性：对常见的几何变换具有一定的鲁棒性

这些特性使得QCT成为视频水印应用中理想的变换域选择。

7. Golden Section Fibonacci Tree Optimization算法

7.1 黄金分割的数学美学与优化原理

黄金分割（Golden Section）是数学中一个具有深刻美学意义的概念，其比值 $\phi = \frac{1 + \sqrt{5}}{2} \approx 1.618$ 在自然界和艺术中广泛存在。从数学角度来看，黄金分割具有独特的自相似性质： $\phi^2 = \phi + 1$ ，这种性质使得黄金分割在优化算法中具有特殊的价值。黄金分割搜索算法是一种基于单峰函数假设的单变量优化方法，它通过逐步缩小搜索区间来逼近最优解。

黄金分割搜索的基本原理是在每次迭代中，将搜索区间按黄金分割比例分为两部分，通过比较分割点处的函数值来决定下一步的搜索方向。设搜索区间为 $[a, b]$ ，两个内部分割点为：

$x_1 = a + (1 - \frac{1}{\phi})(b - a) = a + 0.382(b - a)$$ $$x_2 = a + \frac{1}{\phi}(b - a) = a + 0.618(b - a)$

通过比较 $f(x_1)$ 和 $f(x_2)$ 的大小，可以排除区间的一部分，新的搜索区间长度为原来的 $\frac{1}{\phi} \approx 0.618$ 倍。这种方法的收敛速度是线性的，收敛常数为 $\frac{1}{\phi}$ ，在单变量优化中具有良好的理论性质。

黄金分割搜索的一个重要优势是其鲁棒性。算法不需要计算函数的导数信息，只需要进行函数值比较，因此适用于非光滑、非凸甚至不连续的目标函数。在实际应用中，黄金分割搜索经常作为其他优化算法的组件，用于线搜索或区间缩放。

7.2 斐波那契数列的递归结构与优化应用

斐波那契数列是数学中最著名的递归序列之一，定义为： $F_0 = 0, F_1 = 1, F_n = F_{n-1} + F_{n-2}$ 。斐波那契数列与黄金分割有着密切的联系：当 $n \to \infty$ 时，相邻斐波那契数的比值趋向于黄金分割比：

$\lim_{n \to \infty} \frac{F_{n+1}}{F_n} = \phi$

这种联系使得斐波那契数列在优化算法中具有重要应用。斐波那契搜索算法是黄金分割搜索的一个变种，它使用斐波那契数来确定搜索区间的分割点。与黄金分割搜索相比，斐波那契搜索在有限步数内具有更好的收敛性质。

斐波那契树优化（Fibonacci Tree Optimization, FTO）算法是一种基于斐波那契数列的群体智能优化算法。该算法模拟了斐波那契数列的生长模式，将搜索空间组织成树状结构，每个节点代表一个候选解。算法的核心思想是通过模拟斐波那契数列的递归关系来生成新的候选解：

$x_n = x_{n-1} + x_{n-2} + \epsilon$

其中 $\epsilon$ 是随机扰动项，用于维持种群的多样性。

FTO算法的树状结构使得算法能够在全局搜索和局部搜索之间取得良好的平衡。树的根节点对应于全局最优解的估计，叶节点对应于局部搜索的候选解。通过控制树的深度和分支因子，可以调节算法在探索（exploration）和利用（exploitation）之间的权衡。

7.3 GSFTO算法的设计理念与数学模型

Golden Section Fibonacci Tree Optimization（GSFTO）算法是黄金分割搜索和斐波那契树优化的有机结合，旨在继承两种方法的优势。GSFTO算法的设计理念是将黄金分割的精确性与斐波那契数列的递归结构相结合，构造一种既具有良好收敛性又能维持种群多样性的优化算法。

GSFTO算法的数学模型包含以下几个关键组件：

种群初始化：算法首先在搜索空间中随机初始化$N$个个体，每个个体的位置向量表示为：

$\mathbf{x}i = \mathbf{x}{\min} + \text{rand}(0,1) \cdot (\mathbf{x}{\max} - \mathbf{x}{\min})$

其中 $\mathbf{x}{\min},\mathbf{x}{\max}$ 分别表示搜索空间的下界和上界。

黄金分割更新策略：在每次迭代中，算法使用黄金分割原理来更新个体位置。对于第$i$个个体，其更新公式为：

$\mathbf{x}i^{(t+1)} = \mathbf{x}{\text{best}}^{(t)} + \phi^{-1} \cdot (\mathbf{x}i^{(t)} - \mathbf{x}{\text{best}}^{(t)}) + \mathbf{r}$

其中 $\mathbf{x}_{\text{best}}^{(t)}$ 表示当前最优解， $\mathbf{r}$ 是随机向量，用于维持种群多样性。

斐波那契递归机制：算法引入斐波那契递归机制来生成新的候选解：

$\mathbf{x}{\text{new}} = \alpha \mathbf{x}{F_{n-1}} + \beta \mathbf{x}{F{n-2}} + \gamma \mathbf{x}_{\text{random}}$

其中 $\alpha, \beta, \gamma$ 是权重系数，满足 $\alpha + \beta + \gamma = 1,\mathbf{x}{F{n-1}},\mathbf{x}{F{n-2}}$ 分别表示按斐波那契指标排序的候选解。

适应性参数调节：GSFTO算法采用自适应参数调节机制，根据算法的收敛状态动态调整搜索参数：

$\alpha(t) = \alpha_0 \cdot \exp\left(-\frac{t}{T}\right)$

其中 $\alpha_0$ 是初始参数值，T是最大迭代次数，这种指数衰减策略确保算法从全局搜索逐渐转向局部搜索。

7.4 GSFTO在深度网络优化中的应用

在深度信念网络的训练过程中，GSFTO算法被用于优化网络的权重和偏置参数。传统的梯度下降方法在训练DBN时容易陷入局部最优，而且对初始化敏感。GSFTO算法通过其全局搜索能力，能够为DBN提供更好的参数初始化，从而提高网络的训练效果。

GSFTO在DBN优化中的应用可以形式化为以下优化问题：

$\min_{\Theta} \mathcal{L}(\Theta) = \min_{\Theta} \left[-\sum_{i=1}^{N} \log P(\mathbf{v}_i | \Theta)\right]$

其中 $\Theta = {W, \mathbf{a}, \mathbf{b}}$ 表示DBN的所有参数， $\mathcal{L}(\Theta)$ 是负对数似然损失函数。

GSFTO算法的适应度函数设计为：

$f(\Theta) = \frac{1}{N} \sum_{i=1}^{N} (y_i^* - y_i(\Theta))^2 + \lambda |\Theta|_2^2$

其中第一项是重构误差，第二项是正则化项， $\lambda$ 是正则化系数。

算法的具体执行步骤包括：

种群初始化：随机生成$M$个参数向量组成初始种群
适应度评估：计算每个个体的适应度值
黄金分割更新：使用黄金分割策略更新个体位置
斐波那契重组：应用斐波那契递归关系生成新个体
选择操作：根据适应度值选择下一代种群
收敛判断：检查终止条件，若满足则停止，否则返回步骤2

这种优化策略的优势在于能够有效平衡全局搜索和局部搜索，避免传统梯度方法的局部最优问题，为DBN提供高质量的参数初始化。

8. 技术融合与系统架构

8.1 多技术融合的理论基础

在现代机器学习和信号处理系统中，单一技术往往难以解决复杂的实际问题，多技术融合已成为提升系统性能的重要手段。技术融合的理论基础可以从信息论、优化理论和系统论的角度来理解。从信息论的视角，不同技术往往捕获数据的不同方面的信息，通过融合可以获得更完整的信息描述。从优化理论的角度，多技术融合相当于在更大的假设空间中寻找最优解，理论上能够获得更好的性能。从系统论的视角，技术融合体现了系统的整体性原理，即整体的功能大于各部分功能的简单叠加。

在本论文的技术架构中，AoA网络、DBN、QCT和GSFTO四种技术的融合体现了深度学习、传统信号处理和智能优化的有机结合。这种融合不是简单的技术叠加，而是基于各技术特点的协同设计。AoA网络负责智能的注意力分配，DBN提供强大的特征提取能力，QCT实现高效的频域分析，GSFTO保证参数优化的全局性。

技术融合的数学模型可以表示为一个复合函数：

$y = h(g(f_1(x), f_2(x)), f_3(x), f_4(x))$

其中 $f_1, f_2, f_3, f_4$ 分别表示四种核心技术的映射函数，g表示中间层的融合函数，h表示最终的输出函数。这种层次化的融合结构使得不同技术能够在不同层次上发挥作用，实现功能的互补和增强。

8.2 系统架构的设计原则

视频水印系统的架构设计需要遵循几个重要原则。首先是模块化原则，即将复杂系统分解为相对独立的功能模块，每个模块负责特定的功能，模块间通过明确的接口进行通信。这种设计有利于系统的开发、测试和维护，也便于对单个模块进行优化和替换。其次是层次化原则，即将系统功能按照抽象层次进行组织，低层提供基础功能，高层实现复杂逻辑。这种设计使得系统具有良好的可扩展性和可维护性。

在本论文的系统架构中，整个水印系统可以分为四个主要层次：预处理层、特征提取层、水印处理层和后处理层。预处理层负责视频的格式转换、关键帧提取等基础功能；特征提取层使用DBN和AoA网络提取视频的深层特征；水印处理层在QCT域中进行水印嵌入和提取；后处理层负责视频的重构和质量评估。

系统的数据流可以用以下流程图描述：

8.3 关键帧提取与二进制像素图生成

关键帧提取是视频水印系统的重要组成部分，它直接影响水印的嵌入效率和系统性能。有效的关键帧提取策略应该能够选择出视觉上重要、信息量丰富且具有较强鲁棒性的帧。本系统采用基于内容复杂度和运动信息的关键帧提取方法。

关键帧的重要性评分可以通过以下公式计算：

$\text{Score}(f_i) = \alpha \cdot \text{Complexity}(f_i) + \beta \cdot \text{Motion}(f_i) + \gamma \cdot \text{Texture}(f_i)$

其中 $\text{Complexity}(f_i)$ 表示第i帧的复杂度， $\text{Motion}(f_i)$ 表示运动信息， $\text{Texture}(f_i)$ 表示纹理丰富度， $\alpha, \beta, \gamma$ 是权重系数。

复杂度可以通过图像的梯度信息来衡量：

$\text{Complexity}(f_i) = \frac{1}{MN} \sum_{x=1}^{M} \sum_{y=1}^{N} \sqrt{(\nabla_x f_i(x,y))^2 + (\nabla_y f_i(x,y))^2}$

运动信息可以通过相邻帧间的光流场来估计：

$\text{Motion}(f_i) = \frac{1}{MN} \sum_{x=1}^{M} \sum_{y=1}^{N} \sqrt{u_i(x,y)^2 + v_i(x,y)^2}$

其中 $u_i(x,y),v_i(x,y)$ 分别表示位置 $(x,y)$ 处的水平和垂直光流分量。

二进制像素图的生成是基于深度信念网络的特征分析结果。DBN通过无监督学习提取视频帧的深层特征表示，这些特征包含了像素级的重要性信息。二进制像素图的生成过程可以表示为：

$\text{BinaryMap}(x,y) = \begin{cases} 1, & \text{if } \text{Importance}(x,y) > \tau, \\ 0, & \text{otherwise}. \end{cases}$

其中 $\text{Importance}(x,y)$ 表示位置 $(x,y)$ 的重要性得分， $\tau$ 是阈值参数。

8.4 水印嵌入与提取的数学模型

水印嵌入过程是整个系统的核心，它需要在保证视觉质量的前提下，将水印信息鲁棒地嵌入到视频中。本系统在QCT域中进行水印嵌入，嵌入公式为：

$C_w(u,v) = C(u,v) + \alpha \cdot S(u,v) \cdot W(u,v)$

其中 $C(u,v)$ 表示原始QCT系数， $W(u,v)$ 表示水印信号， $S(u,v)$ 表示AoA网络生成的分数图， $\alpha$ 表示嵌入强度， $C_w(u,v)$ 表示嵌入水印后的QCT系数。

分数图$S(u,v)$的作用是提供自适应的嵌入强度控制。在纹理丰富、视觉不敏感的区域，分数图的值较大，允许更强的水印嵌入；在平滑、视觉敏感的区域，分数图的值较小，限制水印的嵌入强度。这种自适应机制确保了水印在提供鲁棒性的同时保持良好的视觉质量。

水印提取过程是嵌入过程的逆操作：

$W'(u,v) = \frac{C'_w(u,v) - C(u,v)}{\alpha \cdot S(u,v)}$

其中 $C'_w(u,v)$ 表示从可能受到攻击的视频中提取的QCT系数， $W'(u,v)$ 表示提取的水印信号。

为了提高提取的精度，系统还采用了统计检测方法。对于二值水印，可以使用相关检测器：

$\rho = \frac{\sum_{u,v} W(u,v) \cdot W'(u,v)}{\sqrt{\sum_{u,v} W(u,v)^2} \sqrt{\sum_{u,v} W'(u,v)^2}}$

当 $\rho$ 超过预设阈值时，判断水印存在；否则判断水印不存在或已被破坏。

这种基于多技术融合的水印系统架构，通过各技术模块的协同工作，实现了在复杂攻击环境下的鲁棒水印嵌入和提取，为视频版权保护提供了有效的技术解决方案。

9. 总结与展望

9.1 技术创新点总结

本文深入解析了基于混合注意力网络和深度信念网络的鲁棒视频水印技术的基础理论，涵盖了数字水印技术、注意力机制、深度信念网络、四元数曲波变换以及优化算法等多个重要领域的核心概念。通过对这些基础理论的系统性阐述，我们可以清晰地看到现代视频水印技术的理论根基和发展脉络。

论文《DeepSecure watermarking: Hybrid Attention on Attention Net and Deep Belief Net based robust video authentication using Quaternion Curvelet Transform domain》的主要技术创新体现在多个层面。首先，在注意力机制的应用方面，该研究首次将Attention on Attention网络引入视频水印领域，通过门控机制实现了对注意力信息的智能控制，有效解决了传统注意力机制的"盲目性"问题。其次，在特征提取方面，研究采用深度信念网络提取视频帧的深层特征表示，并结合GSFTO优化算法进行参数优化，显著提升了特征提取的质量和效率。第三，在变换域选择方面，四元数曲波变换的应用实现了对彩色视频多通道信息的统一处理，保持了通道间的相关性，提高了水印的鲁棒性。最后，在系统架构方面，多技术融合的设计理念实现了不同技术优势的互补，构建了一个性能优异的视频水印系统。

9.2 理论意义与实际价值

从理论意义来看，这项研究代表了视频水印技术从传统信号处理向深度学习范式的重要转变。传统的水印方法主要依赖于手工设计的特征和启发式的嵌入策略，而基于深度学习的方法能够自动学习最优的特征表示和嵌入策略。特别是注意力机制的引入，使得水印系统具备了类似人类视觉注意力的智能选择能力，能够自适应地关注最重要的视频内容区域。这种从"被动嵌入"到"主动选择"的转变，体现了人工智能技术在传统信号处理领域的深度融合和创新应用。

深度信念网络作为深度学习的重要先驱技术，在视频水印中的成功应用证明了生成式模型在特征学习方面的独特优势。与判别式模型相比，生成式模型能够学习数据的内在分布特征，这对于理解视频内容的语义结构具有重要价值。四元数曲波变换的应用则体现了多维信号处理理论的发展，它不仅能够处理传统的空域和频域信息，还能够有效分析颜色空间的相关性和几何结构的方向性。

从实际应用价值来看，这项研究为解决当前视频版权保护面临的挑战提供了新的技术路径。随着高清视频、4K视频甚至8K视频的普及，传统的水印技术在处理大容量、高分辨率视频时面临着计算效率和存储空间的双重压力。基于深度学习的水印方法通过智能的关键帧选择和自适应的嵌入策略，能够在保证水印质量的前提下显著降低计算复杂度。此外，系统对各种攻击的强鲁棒性使其能够应对复杂的网络传输环境和多样化的恶意攻击，为实际的商业应用提供了可靠的技术保障。

9.3 技术发展趋势与挑战

当前，视频水印技术正朝着更加智能化、自适应化的方向发展。人工智能技术的快速进步为水印领域带来了新的机遇，同时也提出了新的挑战。从技术发展趋势来看，未来的视频水印技术可能会更加注重以下几个方面：

在算法层面，端到端的深度学习框架将成为主流。传统的水印系统通常由多个相对独立的模块组成，模块间的接口设计和参数调优往往需要大量的人工干预。而端到端的深度学习框架能够将整个水印流程统一在一个可微分的网络中，通过梯度下降算法实现全局优化。这种方法不仅能够简化系统设计，还能够获得更好的整体性能。

在计算效率方面，轻量化网络设计将成为重要研究方向。随着移动设备和边缘计算的普及，水印算法需要能够在资源受限的环境中高效运行。这要求研究者在保证算法性能的前提下，尽可能减少模型参数和计算复杂度。知识蒸馏、网络剪枝、量化等技术将在水印领域得到更广泛的应用。

在鲁棒性方面，对抗性训练和元学习技术的应用将进一步提升水印的抗攻击能力。传统的鲁棒性测试通常基于已知的攻击类型，而实际应用中可能面临未知的攻击方式。通过对抗性训练，水印系统能够学习到更加泛化的抗攻击特征；通过元学习，系统能够快速适应新的攻击类型。

然而，技术发展也面临着诸多挑战。首先是安全性挑战，随着深度学习技术的普及，基于神经网络的攻击方法也在不断发展。对抗样本攻击、模型逆向工程等技术可能对基于深度学习的水印系统构成威胁。其次是标准化挑战，目前的深度学习水印方法往往缺乏统一的评估标准和性能基准，这限制了不同方法之间的公平比较和技术进步。最后是可解释性挑战，深度学习模型的"黑箱"特性使得水印系统的决策过程难以理解和解释，这在某些应用场景中可能成为技术采用的障碍。

9.4 未来研究方向

基于当前的技术发展状况和面临的挑战，未来的视频水印研究可能会在以下几个方向取得突破：

多模态水印技术将成为重要的研究方向。现代的多媒体内容往往包含视频、音频、文本等多种模态信息，单一模态的水印可能无法提供足够的安全保障。多模态水印技术通过在不同模态中协同嵌入水印信息，不仅能够提高水印的容量和鲁棒性，还能够实现跨模态的版权保护。这种技术的实现需要深入研究不同模态之间的相关性和互补性，设计有效的多模态融合策略。

区块链与水印技术的结合将为数字版权保护提供新的解决方案。区块链技术的去中心化、不可篡改等特性与水印技术的隐蔽性、鲁棒性形成良好的互补。通过将水印信息的哈希值记录在区块链上，可以实现水印的时间戳认证和不可否认性。同时，智能合约技术可以自动化水印的验证和版权确认过程，降低版权保护的成本和复杂度。

隐私保护水印将成为重要的研究方向。随着隐私保护意识的增强和相关法规的完善，传统的水印技术可能面临隐私泄露的风险。差分隐私、同态加密等隐私保护技术与水印技术的结合，能够在保护内容版权的同时保护用户隐私。这种技术的发展需要在版权保护强度、隐私保护程度和系统性能之间找到合适的平衡点。

关于实验验证部分，由于篇幅限制，本文主要聚焦于基础理论的深度解析。该论文的详细实验结果、性能评估和比较分析可以参考原始论文《DeepSecure watermarking: Hybrid Attention on Attention Net and Deep Belief Net based robust video authentication using Quaternion Curvelet Transform domain》，其中包含了在多个标准数据集上的全面实验验证，以及与现有先进方法的详细性能比较。

通过对这些基础理论的深入理解，我们可以更好地把握视频水印技术的发展脉络和未来趋势，为相关研究和应用提供理论指导和技术支撑。随着人工智能技术的不断发展，相信视频水印技术将在保护数字内容版权、维护网络信息安全方面发挥越来越重要的作用。