差分约束系统SPFA判负环
什么是差分约束系统?
差分约束可以理解为满足n个条件的不等式。通常属于
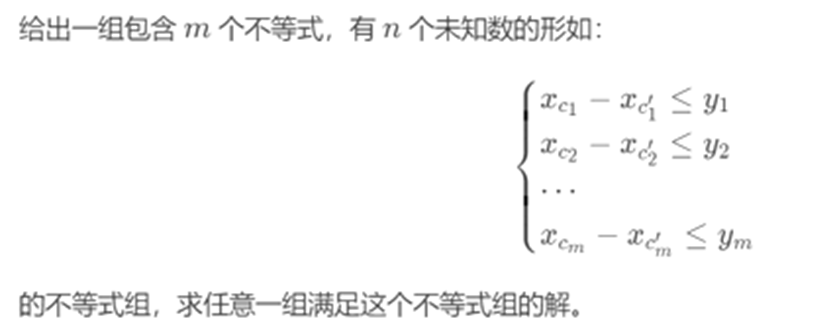
为什么能用spfa?
1.每个不等式能转化为一条有向边,比如可以转化为从节点i到j有一条权为n的边
2.求解差分约束系统等价于寻找一组变量值 x_1, x_2, ..., x_n,满足所有边对应的约束。这与最短路松弛操作的逻辑完全一致:
最短路中,dist[j] ≤ dist[i] + c(从 i 到 j 的最短路径不超过 i 的距离加边权 c)
差分约束中,x_j ≤ x_i + c(变量 x_j 不超过 x_i 加常数 c)
———————————————————————————————————————————
如何根据不等式建边?
对于任意不等式 x_j - x_i ≤ c(这是最基础的形式):
1.等价变形为 x_j ≤ x_i + c
2.对应图中一条从节点 i 指向节点 j 的有向边,边的权重为 c
为什么如此?
因为spfa的松弛操作对应“如果dist[i]>d[x]+w[i]就更新”,这个不等式相当于x_j ≤ x_i + c
所有建边规则的本质,都是把差分约束的不等式,统一转化为最短路算法能理解的 “dist[j] ≤ dist[i] + c” 形式。只有这样,才能通过 SPFA 等最短路算法,既找到满足所有约束的x(即dist数组),又能检测负环(判断无解)。
——————————————————————————————————————————
为什么负环无解?
在差分约束系统中,负环的存在会导致无限满足 “变量差值小于某个负数” 的矛盾循环,使得变量取值不存在合法解。
具体来说,差分约束将每个不等式 x_j - x_i ≤ c 转化为图中从 i 到 j、边权为 c 的有向边,求解等价于找一组变量值满足所有边的约束。若图中存在负环(环上所有边权之和为负数),则沿着环循环遍历会得到矛盾:
- 例如负环 a→b→c→a,边权分别为 -1、-1、-1,对应约束 x_b - x_a ≤ -1、x_c - x_b ≤ -1、x_a - x_c ≤ -1。
- 将三个不等式相加,左边抵消为 0,右边总和为 -3,得到 0 ≤ -3,这是恒不成立的矛盾。
- 同时,绕负环循环次数越多,变量差值会无限减小(如 x_b 会比 x_a 无限小),无法找到固定的合法数值,因此系统无解。
——————————————————————————————————————————
如何spfa判负环?
判断任意一个节点入队次数是否大于总节点数。因为存在负环会让spfa判断两点间权时每经过一次就让总和越变越小,于是重复更新,重复入队
来看代码
bool spfa(int s1) {for(int i = 1; i <= n+1; i++) {dis[i] = 2147483647;cnt[i] = 0;inq[i] = false;}dis[s1] = 0;q.push(s1);inq[s1] = true;cnt[s1]++;int x;while(!q.empty()) {x = q.front();q.pop();inq[x] = false;for(int i = head[x]; i; i = ne[i]) {if(dis[to[i]] > dis[x] + w[i]) {dis[to[i]] = dis[x] + w[i];if(!inq[to[i]]) {q.push(to[i]);inq[to[i]] = true;cnt[to[i]]++;if(cnt[to[i]] > n) {return true;}}}}}return false;
}很常规,如果你不知道基础的spfa,可以看一下前几期的博客最短路spfa和多层图(P1073 [NOIP 2009 提高组] 最优贸易)题解-CSDN博客
———————————————————————————————————————————
很好,既然如此,我们来写一道模板
P5960 【模板】差分约束 - 洛谷

先来看一下如何建边,我们得到的等式是差小于一个常数。根据我们上面梳理的内容,我们要先转化为一个数小于等于一个和。也就是x_c1≤x_c1'+y_1
令x_c1=a,x_c1'=b,y1=c,所以我们对于第一个等式,建边就是add(b,a,c)
同时,我们要建立一个“超级节点”,确保这个节点和整个图上的所有节点都有边相连,因为图不一定是连通图,spfa有可能扫不到有些点
差不多这样,AC代码
#include<bits/stdc++.h>
using namespace std;int read(){int s=0,fl=1;char w=getchar();while(w>'9'||w<'0'){if(w=='-')fl=-1;w=getchar();}while(w<='9'&&w>='0'){s=s*10+(w^48);w=getchar();}return fl*s;
}
void out(int x){if(x<0)putchar('-'),x=-x;if(x<10)putchar(x+'0');else out(x/10),putchar(x%10+'0');
}
int n,m;
bool inq[100010];
int head[100010],to[100010],ne[100010],w[100010],tot;
int dis[100010],cnt[100010];
queue<int>q;
void add(int x,int y,int v){to[++tot]=y;ne[tot]=head[x];head[x]=tot;w[tot]=v;
}
bool spfa(int s1) {for(int i = 1; i <= n+1; i++) {dis[i] = 2147483647;cnt[i] = 0;inq[i] = false;}dis[s1] = 0;q.push(s1);inq[s1] = true;cnt[s1]++;int x;while(!q.empty()) {x = q.front();q.pop();inq[x] = false;for(int i = head[x]; i; i = ne[i]) {if(dis[to[i]] > dis[x] + w[i]) {dis[to[i]] = dis[x] + w[i];if(!inq[to[i]]) {q.push(to[i]);inq[to[i]] = true;cnt[to[i]]++;if(cnt[to[i]] > n) {return true;}}}}}return false;
}int main(){n=read();m=read();for(int i=1;i<=m;i++){int a,b,c;a=read();b=read();c=read();add(b,a,c);}for(int i=1;i<=n;i++){add(n+1,i,0);}if(spfa(n+1)){cout<<"NO";return 0;}for (int i = 1; i <= n; i++){printf("%d ", dis[i]);}return 0;
}双倍经验
P1993 小 K 的农场 - 洛谷

国际惯例先骗分,全输出No有85分
来正经做
根据题目,我们能列出三个不等式
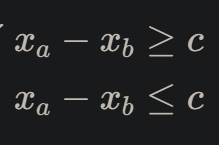
还有一个就是相等,移项后可得一个减去另一个=0;也就是这条边的边权为0
其实就很简单了,建图要满足第一个等式,我们只需要两边都乘上-1就能改变不等号的方向。
直接上代码吧,其他都是一样的
#include<bits/stdc++.h>
using namespace std;int read(){int s=0,fl=1;char w=getchar();while(w>'9'||w<'0'){if(w=='-')fl=-1;w=getchar();}while(w<='9'&&w>='0'){s=s*10+(w^48);w=getchar();}return fl*s;
}
void out(int x){if(x<0)putchar('-'),x=-x;if(x<10)putchar(x+'0');else out(x/10),putchar(x%10+'0');
}
int n,m,a,b,c,tot;
int head[1000010],ne[1000010],to[1000010],w[1000010];
int d[1000010],cnt[1000010];
bool inq[1000010];
queue<int>q;
void add(int x,int y,int c){to[++tot]=y;ne[tot]=head[x];head[x]=tot;w[tot]=c;
}
bool spfa(int s){for(int i=1;i<=n+1;i++){d[i]=1e18;inq[i]=false;cnt[i]=0;}d[s]=0;q.push(s);inq[s]=true;cnt[s]++;int x;while(!q.empty()){x=q.front();q.pop();inq[x]=false;for(int i=head[x];i;i=ne[i]){if(d[to[i]]>w[i]+d[x]){d[to[i]]=w[i]+d[x];if(!inq[to[i]]){q.push(to[i]);inq[to[i]]=true;cnt[to[i]]++;if(cnt[to[i]]>n){return true;}}}}}return false;
}
int main(){n=read();m=read();for(int i=1;i<=m;i++){int op=read();if(op==1){a=read();b=read();c=read();add(a,b,-c);}else if(op==2){a=read();b=read();c=read();add(b,a,c);}else{a=read();b=read();add(a,b,0);add(b,a,0);}}for(int i=1;i<=n;i++){add(n+1,i,0);}if(spfa(n+1)){cout<<"No";return 0;}cout<<"Yes";return 0;
}