Lec. 2： Pytorch, Resource Accounting 课程笔记

本节概述

讨论训练模型所需的所有原语（primitives)
自下而上地从张量到模型，再到优化器再到训练循环。
密切关注效率
特别讨论：
内存（GB）
计算（FLOP）

启发性问题

问题1

在1024个H100上的15T tokens训练70B的模型需要多长时间
total_flops =6 * 70e9 * 15e12(本节课会介绍)
h100_flop_per_sec == 1979e12 / 2(H100每秒的flops)
mfu = 0.5
flops_per_day = h100_flop_per_sec * mfu * 1024 * 60 * 60 * 24(H100每天的flops)
天数=total_flops / flops_per_day

问题2

使用AdamW在八个H100上能训练的最大模型是什么？
H100有80个GB=80e9 bytes
每个参数的字节： bytes_per_parameter = 4 + 4 + （4 + 4） 参数、梯度、优化器状态（AdamW 需要存储两个状态（动量和方差），各 4 字节，共 8 字节）
最大参数数量 = 总显存 ÷ 每个参数所需字节数：num_parameters = (h100_bytes * 8) / bytes_per_parameter=40B

我们天真地将 float32 用于参数和梯度。我们还可以使用 bf16 作为参数和梯度 （2 + 2），并保留参数 （4） 的额外 float32 副本。这不会节省内存，但速度更快。

内存核算

张量是存储所有内容的基本构建块：参数、梯度、优化器状态、数据、激活。

多种方式创建张量：
93 x = torch.tensor([[1., 2, 3], [4, 5, 6]])
94 x = torch.zeros（4， 8） # 4x8 全0矩阵
95 x = torch.ones（4， 8） # 4x8 全1矩阵
96 x = torch.randn（4， 8） # 4x8的二维张量 每个元素都是独立同分布的随机数，符合正态分布（均值为0，标准差为1）

分配未初始化值的：
x = torch.empty(4, 8)

张量内存

几乎所有内容（参数、梯度、激活、优化器状态）都存储为浮点数。

float32（存储优化器状态和参数必须使用）

float32 数据类型（也称为 fp32 或单精度）是默认值。
传统科学计算中，float32是基线，也可以使用双精度(float64)
但一般在深度学习中，flaot32是最大值
内存由每个值的 （i） 值数量和 （ii） 数据类型决定。

假设创建了一个4x8的0矩阵
默认情况下会使用float32
元素个数为32，每个元素大小为4字节(32位=4字节)
内存使用=4*8*4=128字节

在GPT-3前馈层的一个矩阵
(12288x4x12288)x4≈2.3GB
所以我们希望它们变得更小使用更少的内存

float16

float16 数据类型（也称为 fp16 或半精度）会减少内存。
1e-8的数在float16下会变成0
如果在训练时发生这种情况，可能会变得不稳定。

bfloat16（通常用于计算）

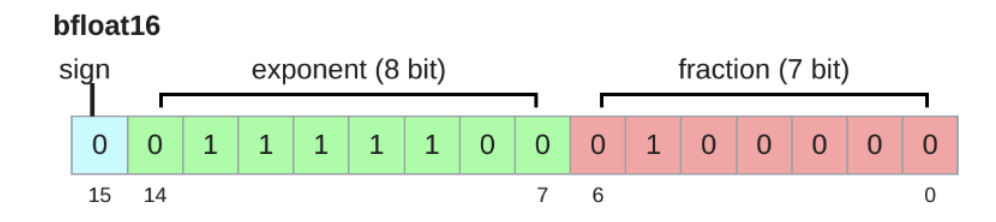
Google Brain 在 2018 年开发了 bfloat（大脑浮点）来解决这个问题。
bfloat16 使用与 float16 相同的内存，但具有与 float32 相同的动态范围！
唯一的问题是分辨率更差，但这对于深度学习来说并不重要。
相同的1e-8在bfloat16下

fp8

2022 年，在机器学习工作负载的推动下，FP8 实现了标准化。

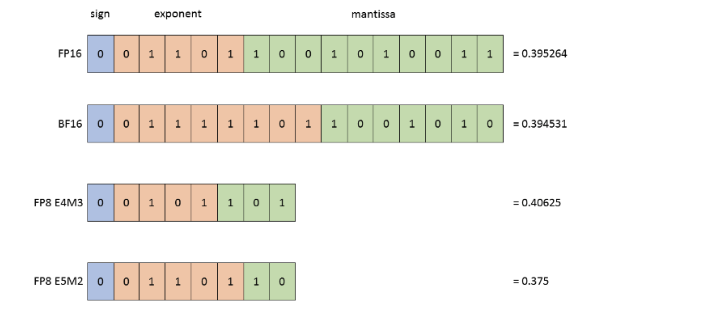
H100 支持 FP8 的两种变体：E4M3（范围 [-448， 448]）和 E5M2（[-57344， 57344]）。
取决于想要更高的分辨率或者更大的动态范围

总结

使用 float32 进行训练是有效的，但需要大量内存。
使用 fp8、float16 甚至 bfloat16 进行训练是有风险的，并且可能会变得不稳定。
解决方案（稍后）：使用混合精度训练

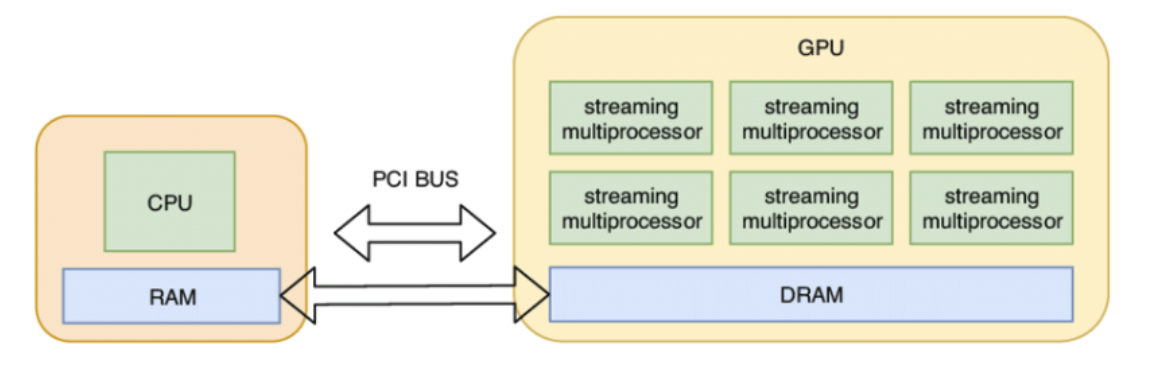
GPU中的张量

默认情况下，张量存储在 CPU 内存中。
然而，为了利用 GPU 的大规模并行性，我们需要将它们移动到 GPU 内存中。

张量操作

大多数张量是通过对其他张量执行操作而创建的。
每个操作都有一些内存和计算结果。

张量存储

PyTorch 中的张量是什么？
PyTorch 张量是指向已分配内存的指针，使用描述如何获取张量任何元素的元数据。

张量切片

许多操作只是提供了张量的不同视图 。
这不会制作副本，因此一个张量的突变会影响另一个张量。
y = x.transpose(1, 0).contiguous().view(2, 3)# 交换张量x的第0、1维并保证他们连续后，将张量重塑为2行3列的形状并赋值给y
view不需要消耗内存和计算，但是contiguous或者reshape会消耗

张量逐元素计算

这些运算对张量的每个元素应用一些运算并返回相同形状的（新）张量。
torch.equal(x.pow(2), torch.tensor([1, 16, 81]))

• x.pow(2) 表示对张量 x 中的每个元素进行平方运算

• torch.tensor([1, 16, 81]) 是一个包含三个元素的张量

• torch.equal() 函数用于检查两个张量的形状和所有元素是否都完全相同

• x.sqrt() 计算每个元素的平方根，结果应为 [1, 2, 3]

• x.rsqrt() 计算每个元素平方根的倒数，结果应为 [1, 1/2, 1/3]

• x + x 实现张量与自身的加法，等同于每个元素乘以 2

• x * 2 直接将张量每个元素乘以 2

• x / 0.5 通过除以 0.5 实现与乘以 2 相同的效果

张量矩阵乘法

一般来说，我们对批次中的每个样本以及序列中的每个标记执行操作。

张量操作库einops

Einops 是一个用于作命名维度的张量的库,它的灵感来自爱因斯坦求和符号
命名所有维度，而不是本质上依赖索引

张量浮点运算次数

浮点运算 （FLOP） 是一种基本运算，如加法 （x + y） 或乘法 （x y）。
两个非常令人困惑的首字母缩略词（发音相同！
FLOPs：浮点运算（完成计算的度量）
FLOP/s：每秒浮点运算（也写作 FLOPS），用于测量硬件的速度。

直觉

训练 GPT-3 （2020） 花费了 3.14e23 次 FLOPs。
GPT-4 （2023） 据推测将需要 2e25 FLOP
美国行政命令：任何以 >= 1e26 FLOP 训练的基础模型都必须向政府报告（2025 年撤销）
A100 的峰值性能为 312 teraFLOP/s(312e12)
H100 的峰值性能为 1979 teraFLOP/s，非稀疏性条件下的峰值性能为50%
h100_flop_per_sec == 1979e12 / 2

8 个 H100 2 周：
total_flops = 8 * (60 * 60 * 24 * 7) * h100_flop_per_sec=4.788e21

线性模型

n个点，每个点d个维度
线性模型将每个 d 维向量映射到 k 个输出

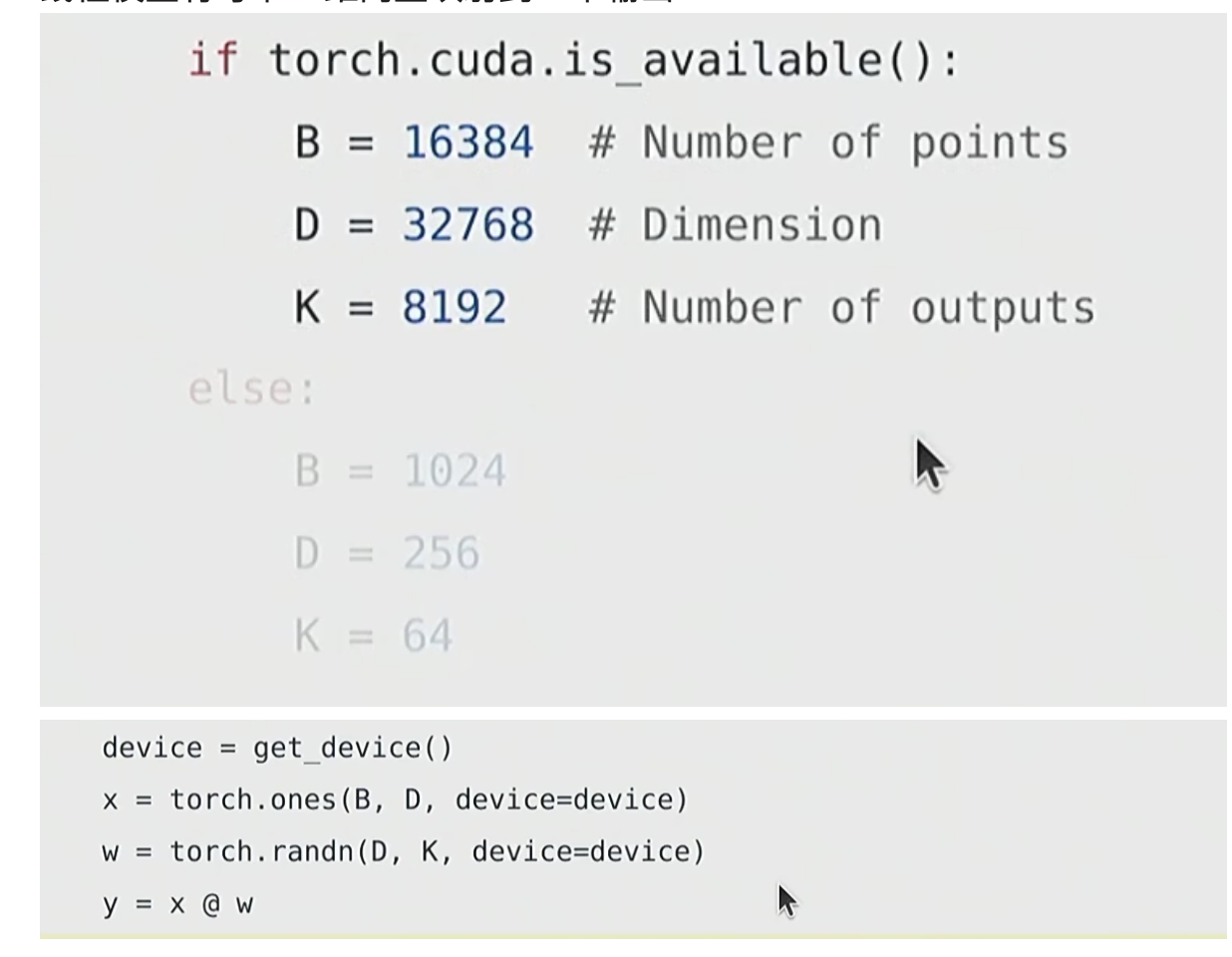
对于每个(i,j,k)三元组，我们都有乘法（$x[i][j]\ast w[j][k]$)
actual_num_flops = 2 * B * D * K

• 运算细节：矩阵乘法的本质是嵌套运算，对于输出y[i][k]（第i个样本的第k个输出），其值为：
  y[i][k] = x[i][0]*w[0][k] + x[i][1]*w[1][k] + ... + x[i][D-1]*w[D-1][k]
  即每个(i, k)位置需要做D次乘法和D-1次加法。
• 总运算量：
  • 对所有B个样本、K个输出，总乘法次数为B * D * K（每个(i, j, k)三元组一次乘法）。
  • 总加法次数约为B * D * K（近似认为加法次数与乘法次数相等，因D-1 ≈ D当D较大时）。
  • 因此，总浮点运算次数为2 * B * D * K（乘法 + 加法各算 1 次 FLOP）。

其他操作的FLOPs

对于一个 m×n 的矩阵（包含 m×n 个元素）：

• 当进行逐元素运算时（例如对矩阵中每个元素取平方，或两个同维度矩阵对应元素相加），每个元素都需要 1 次浮点运算。
• 因此，总运算量为元素总数，即 m×n 个 FLOP，用复杂度表示就是 O(mn)（大 O 符号描述算法复杂度的量级）。
  以 “两个 m×n 矩阵相加” 为例：
• 两个矩阵相加时，需将第一个矩阵的第 i 行第 j 列元素与第二个矩阵的对应位置元素相加，得到结果矩阵的对应元素。
• 整个过程需要对 m×n 对元素进行加法运算，共 m×n 次浮点运算，因此符合 “需要 mn 个 FLOP” 的结论。
  一般来说，在深度学习中遇到的其他运算都比足够大的矩阵的矩阵乘法更昂贵。

请注意，FLOP/s 在很大程度上取决于数据类型！

模型 FLOP 利用率 （MFU）

定义：（实际 FLOP/s）/（承诺的 FLOP/s）[忽略通信/开销]
通常，>= 0.5 的 MFU 相当不错（如果 matmuls 占主导地位，则会更高）

让我们用 bfloat16 来做：
这里的 MFU 相当低，可能是因为承诺的 FLOP 有点乐观。

矩阵乘法占主导地位：（2 m n p） FLOP
FLOP/s 取决于硬件（H100 >> A100）和数据类型（bfloat16 >> float32）
模型 FLOP 利用率 （MFU）：（实际 FLOP/s）/（承诺的 FLOP/s）

梯度基础

到目前为止，我们已经构造了张量（对应于参数或数据）并通过运算（向前）传递它们。
现在，我们将计算梯度（向后）。

梯度FLops

重新审视我们的线性模型

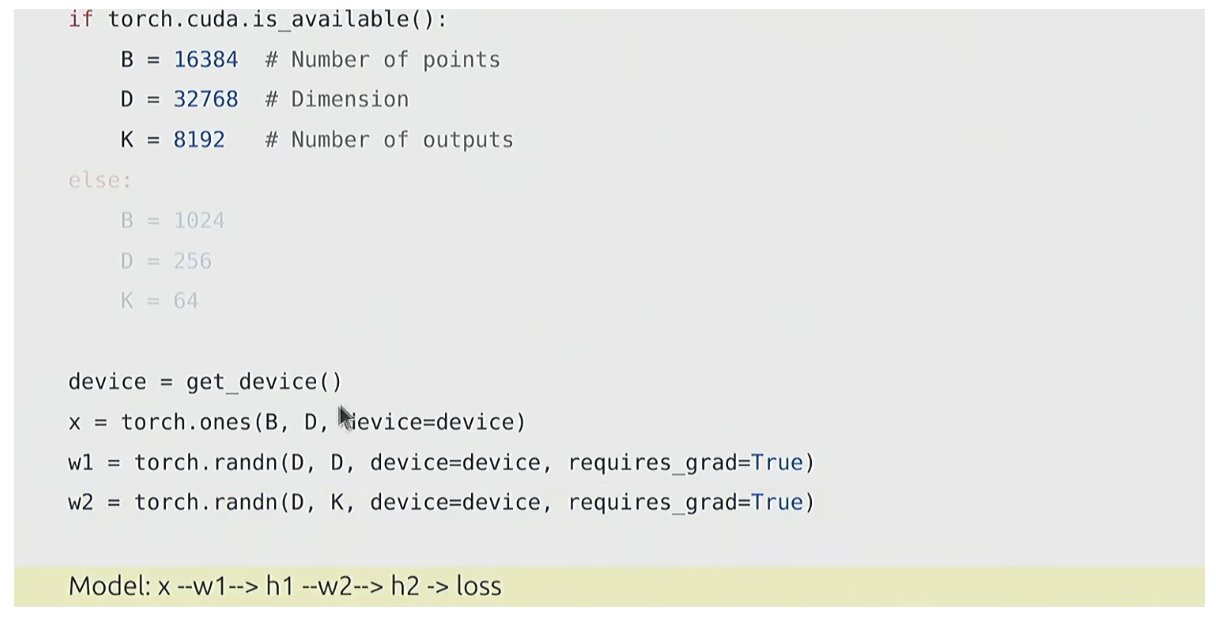
正向计算的FLOPs

• 第一层：输入x（维度可简化为B×D）与w1（D×D）相乘，得到h1（B×D）。每个元素的计算需要D次乘法 +D-1次加法，近似为2×B×D×D（忽略常数项-1）；
• 第二层：h1（B×D）与w2（D×K）相乘，得到h2（B×K）。同理，计算量约为2×B×D×K。
  两者相加即得到总正向 FLOPs：num_forward_flops = 2*B*D*D + 2*B*D*K。

反向计算的FLOPs:

1. 计算 w2.grad（权重梯度）

根据链式法则，w2.grad[j,k] 的计算式为：

$(w2.grad[j,k]={\sum }_{i=1}^{B}h1[i,j]\cdot h2.grad[i,k])$

• 数学操作： 对每个 (j,k) 元素，需计算 B 次乘法和 B-1 次加法（累加）。 单元素 FLOPs：2B（近似，忽略 B-1 与 B 的差异） 总元素数：D×K 总 FLOPs：2B × D×K = 2B D K

2. 计算 h1.grad（隐藏层梯度）

链式法则下，h1.grad[i,j] 的计算式为：
$(h1.grad[i,j]={\sum }_{k=1}^{K}w2[j,k]\cdot h2.grad[i,k])$

• 数学操作： 对每个 (i,j) 元素，需计算 K 次乘法和 K-1 次加法。 单元素 FLOPs：2K 总元素数：B×D 总 FLOPs：2K × B×D = 2B D K

3. 计算 w1.grad（第一层权重梯度）

类似地，w1.grad[j,l] 的计算式为：
$(w1.grad[j,l]={\sum }_{i=1}^{B}x[i,l]\cdot h1.grad[i,j])$

• 数学操作： 对每个 (j,l) 元素，需计算 B 次乘法和 B-1 次加法。 单元素 FLOPs：2B 总元素数：D×D 总 FLOPs：2B × D×D = 2B D²

4. 计算 x.grad（输入梯度）

若需要计算输入梯度，公式为：
$(x.grad[i,l]={\sum }_{j=1}^{D}w1[j,l]\cdot h1.grad[i,j])$

• 数学操作： 对每个 (i,l) 元素，需计算 D 次乘法和 D-1 次加法。 单元素 FLOPs：2D 总元素数：B×D 总 FLOPs：2D × B×D = 2B D²

总结

前向传播约为2*数据*参数 FLOPs
反向传播约为:4*数据*参数 FLOPs

总计6*数据*参数 FLOPs

模型参数

模型参数在 PyTorch 中存储为 nn。参数对象。
输入维度16384
输出维度32
w = nn.Parameter(torch.randn(input_dim, output_dim))

数据初始化

x = nn.Parameter(torch.randn(input_dim))
output = x @ w # @inspect output
请注意， 输出的每个元素都按 sqrt（input_dim）： 18.919979095458984 缩放。
大值会导致梯度爆炸并导致训练不稳定。
为此，我们只需重新缩放 1/sqrt（input_dim）

w = nn.Parameter(torch.randn(input_dim, output_dim) / np.sqrt(input_dim))
output = x @ w # @inspect output
现在输出的每个元素都是恒定的：-1.5302726030349731。

自定义模型

使用nn.Parameter建立一个简单的深度线性模型。

随机性注意事项

随机性出现在许多地方：参数初始化、删除、数据排序等。
为了可重现性，我们建议您始终为每次使用随机性传入不同的随机种子。
确定性在调试时特别有用，因此您可以找到错误。
为了安全起见，有三个地方可以设置随机种子，您应该同时完成所有操作。

# Torch
seed = 0
torch.manual_seed(seed)
# NumPy
import numpy as np
np.random.seed(seed)
# Python
random.seed(seed)

数据加载

在语言建模中，数据是整数序列（由分词器输出）。
将它们序列化为 numpy 数组（由分词器完成）很方便。
orig_data = np.array([1, 2, 3, 4, 5, 6, 7, 8, 9, 10], dtype=np.int32)
如果不想一次将整个数据加载到内存中(LLaMA data is 2.8TB).
使用 memmap 仅将访问的部分延迟加载到内存中。
data = np.memmap(“data.npy”, dtype=np.int32)

优化器

让我们定义 AdaGrad 优化器
动量 = SGD + 梯度的指数平均
AdaGrad = SGD + 按梯度平方平均
RMSProp = AdaGrad + 梯度平方的指数平均
Adam = RMSProp + 动量

检查点

训练语言模型需要很长时间，而且肯定会崩溃。你不想失去所有的进度。
在训练期间，定期将模型和优化器状态保存到磁盘非常有用。

混合精度训练

数据类型（float32、bfloat16、fp8）的选择需要权衡。
更高的精度：更准确/更稳定、内存更多、计算更多
精度较低：精度/稳定性较低、内存较少、计算量较少

我们怎样才能两全其美？

解决方案：默认使用 float32，但尽可能使用 {bfloat16， fp8}。

具体：
使用 {bfloat16， fp8} 进行前向传递（激活）。
其余部分（参数、渐变）使用 float32。

总结

问题1：训练模型时，总浮点运算量（FLOPs）如何计算？

总FLOPs约为6×数据量×参数量。其中前向传播占2×数据量×参数量，反向传播（含梯度计算）占4×数据量×参数量。

问题2：在给定硬件（如H100）上，如何估算训练模型的时间？

需先计算总FLOPs，再结合硬件性能（如H100的有效FLOP/s，约为1979e12/2，考虑非稀疏性）、模型FLOP利用率（MFU，通常取0.5）及设备数量，公式为：时间=总FLOPs÷（单设备有效FLOP/s×MFU×设备数量）。

问题3：使用AdamW优化器时，如何确定硬件可支持的最大模型参数？

每个参数需存储参数（4字节）、梯度（4字节）及优化器状态（动量和方差，共8字节），总计16字节。最大参数量=总显存÷16字节。例如8个80GB H100，总显存640GB，最大参数约40B。

问题4：深度学习中常用的浮点数据类型（float32、bfloat16、fp8）各有何特点？

float32（4字节）精度高，适合存储参数和优化器状态；bfloat16（2字节）动态范围与float32一致，分辨率较低，适合计算；fp8（1字节）内存占用最小，分E4M3（高分辨率）和E5M2（大动态范围），需平衡精度与效率。

问题5：什么是模型FLOP利用率（MFU）？其典型值为何？

MFU是实际FLOP/s与硬件理论峰值FLOP/s的比值，反映硬件效率。通常MFU≥0.5即为较优，矩阵乘法占比越高，MFU越接近理论值。

问题6：混合精度训练的核心思想是什么？

结合不同精度优势，用低精度（如bfloat16、fp8）进行前向计算（激活）以节省内存和提升速度，用高精度（如float32）存储参数、梯度和优化器状态以保证训练稳定性。