Hybrid Beamforming Design for OFDM Dual-Function Radar-Communication System

摘要—采用正交频分复用（OFDM）的雷达通信双功能（DFRC）系统能够高效利用频谱，同时在通信方面保持对多径衰落的可靠鲁棒性，并提升雷达的估计精度。然而，采用全数字波束赋形架构（即每根天线都配备一个射频（RF）链）的成本高昂。这促使我们在本工作中考虑将混合波束赋形应用于OFDM-DFRC系统。具体而言，我们通过联合优化通信的频谱效率（SE）和雷达的空间谱匹配误差（SSME），来同时设计 用于整个带宽的模拟波束赋形器 和用于 每个子载波的数字波束赋形器 。为了解决由此产生的优化问题，我们设计了一种基于共识的乘子交替方向法（consensus-ADMM）。此外，从实践角度出发，我们考虑了使用有限分辨率移相器进行混合发射波束赋形设计的问题，以促进模拟波束赋形器的经济实现。最后，通过数值仿真验证了所提方案的有效性。

索引术语—OFDM-DFRC，混合波束赋形，多用户，共识乘子交替方向法（consensus-ADMM），有限分辨率移相器。

由于对无线通信设备的需求日益增长，无线设备的射频（RF）频谱拥塞问题变得越来越严重。雷达系统的频谱与无线设备的频谱发生了重叠。例如，长期演进（LTE）和WiMax系统的频段接近3.4 GHz频段，该频段与S波段雷达系统部分重叠 [1]。全球移动通信系统（GSM）使用1710–1880 MHz频段 [2]，该频段可能与特高频（UHF）雷达系统共享。因此，美国国防高级研究计划局（defense advanced research projects agency，DARPA）提出了雷达与通信共享频谱接入（SSPARC）项目 [3], [4]。

雷达-通信频谱共享（RCSS）的一种巧妙方法是设计频谱兼容的波形，并将期望的频谱零点导向其他设备。因此，雷达系统对这些设备产生的干扰能量被限制在可接受的水平 [5]–[8]。例如，在[7]中，通过最大化信干噪比（SINR）并对重叠频段内的能量施加约束，为相控阵-雷达设计了一种频谱兼容波形。该方法随后在[8]中被扩展到多输入多输出（MIMO）雷达。这些工作中构建的波形设计问题是非凸的，并通过例如最小方差无失真响应和对偶上升法（MVDR-DAM）等方法进行次优求解。需要注意的是，在无线设备频谱间隔较大的场景中，这些设计的性能并不理想。除了波形之外，还应联合设计其他方面以实现频谱共享 [9]–[14]。具体来说，[10]研究了雷达采样方案和通信码本的协同设计问题，以实现MIMO通信和MIMO矩阵补全（MIMO-MC）雷达的共存。通过联合优化雷达脉冲编码和通信编码矩阵，[12]解决了在信号相关干扰存在下，脉冲雷达与通信系统的共存问题。

与上述协同设计不同，在雷达通信双功能（DFRC）系统中，雷达和通信共享同一平台。近年来，这类系统备受关注 [15]–[27]。一项处理该问题的早期工作考虑了单天线 [15]。然而，由于缺少自由度（DOFs），单天线架构的DFRC系统在雷达和通信方面的性能都有限。因此，近期的研究更多地集中在MIMO系统的双功能设计上。例如，在 [19]中，为MIMO雷达设计了一种双功能波束方向图。通信的信息比特被嵌入到旁瓣电平中，而主瓣则用于支持目标检测。为了提高通信的数据速率，在 [21]中，利用跳频码来生成正交波形，并将一个相移键控通信符号嵌入到每个正交波形中。此外，[24]中优化了一种折衷波形，用于同时探测雷达目标并与下行链路的蜂窝用户通信。最近，[27]中提出了一种基于跳频（frequency-hopping，FH）MIMO雷达的波形，用于DFRC系统中的时序偏移和信道估计。

需要注意的是，上述方法是为DFRC系统开发的，它们采用了全数字波束赋形，即每根天线都需要一条独立的射频链。众所周知，这种架构会导致高昂的硬件成本和功耗，尤其是在大规模阵列中，例如毫米波（mmWave）系统。对于通信系统，针对单用户（SU）和多用户（MU）场景的模拟/数字混合波束赋形设计已得到广泛研究 [28]–[37]。开创性的工作 [28] 提出了一种混合预编码设计，适用于射频链数量大于数据流数量两倍的情况。然而，一般情况下的解决方案仍是一个悬而未决的问题。在 [29]中，通过利用毫米波信道的稀疏特性，为单载波 SU-MIMO系统设计了一种混合预编码算法。此外，[32] 提出了一种“两阶段”方法来为毫米波单载波SU-MIMO系统设计混合预编码器。在该方法中，首先获得最优的全数字预编码器，然后设计混合预编码器以逼近全数字预编码器。[35]中的结果表明，对于单载波MU-MIMO系统，当射频链的数量是数据流数量的两倍时，混合预编码器能够达到与全数字预编码器相当的性能。作为一项进一步的工作，[36]中考虑了为采用低分辨率移相器的单载波MU-MIMO系统设计混合预编码器和合并器。与传统的模拟/数字混合波束赋形相比，该方案提供了更低的硬件成本。

上面讨论的混合波束赋形设计假设信道是平坦衰落的。然而，对于宽带正交频分复用（OFDM）系统，信道是频率选择性的。在这种情况下，主要的挑战是，尽管数字波束赋形可以基于每个子载波进行优化，但模拟波束赋形的优化只能将整个宽带作为一个整体来考虑。这个问题在 [38] 和 [39] 中得到了研究。具体来说，[38]为宽带SU-OFDM系统设计了有限反馈混合预编码，其中考虑了频率选择性信道。在[39]中，提出了用于采用OFDM调制的SU-MIMO和MU-MISO系统的混合波束赋形设计。

事实上，DFRC系统也期望采用宽带OFDM调制，因为它能够同时提高通信的可达速率和雷达目标探测的精度。然而，现有的关于OFDM系统混合波束赋形的研究工作只关注通信方面。要实现宽带OFDM-DFRC系统，有许多问题需要解决。例如，如何基于采用混合波束赋形结构的OFDM调制信号来实现期望的雷达功能？此外，DFRC系统的混合波束赋形是一个双目标问题。研究通信和雷达之间的性能权衡具有重要意义。这些事实促使我们开展当前的工作，在我们的工作中，数字波束赋形针对每个子载波进行优化，而模拟波束赋形则针对整个带宽进行优化。

本工作的主要贡献可总结如下：

• 通过考虑发射DFRC系统和用户之间的宽带频率选择性信道，推导了具有混合波束赋形架构的OFDM-DFRC系统的信号方案。针对该系统，我们构建了基于加权优化的混合波束赋形设计问题。因此，它可以在通信和雷达性能之间提供灵活的权衡。
• 为了解决非凸优化问题，提出了一种交替优化方法。具体来说，对于混合发射机的设计，我们假设接收机是全数字的。在设计好的混合发射机基础上，接着对混合接收机进行优化。为了处理发射机设计，我们采用了一种基于共识乘子交替方向法（consensus-ADMM）框架[40]的分布式方法。此外，模拟波束赋形器是通过利用块坐标下降（BCD）方法[41], [42]获得的。
• 为了促进OFDM-DFRC系统的低成本实现，我们考虑使用有限分辨率移相器来实现模拟波束赋形器。特别地，带有有限分辨率移相器的混合发射机是通过最小化未量化波束赋形器和量化后的波束赋形器之间的差异来进行优化的。

II. SYSTEM MODEL AND PROBLEM FORMULATION

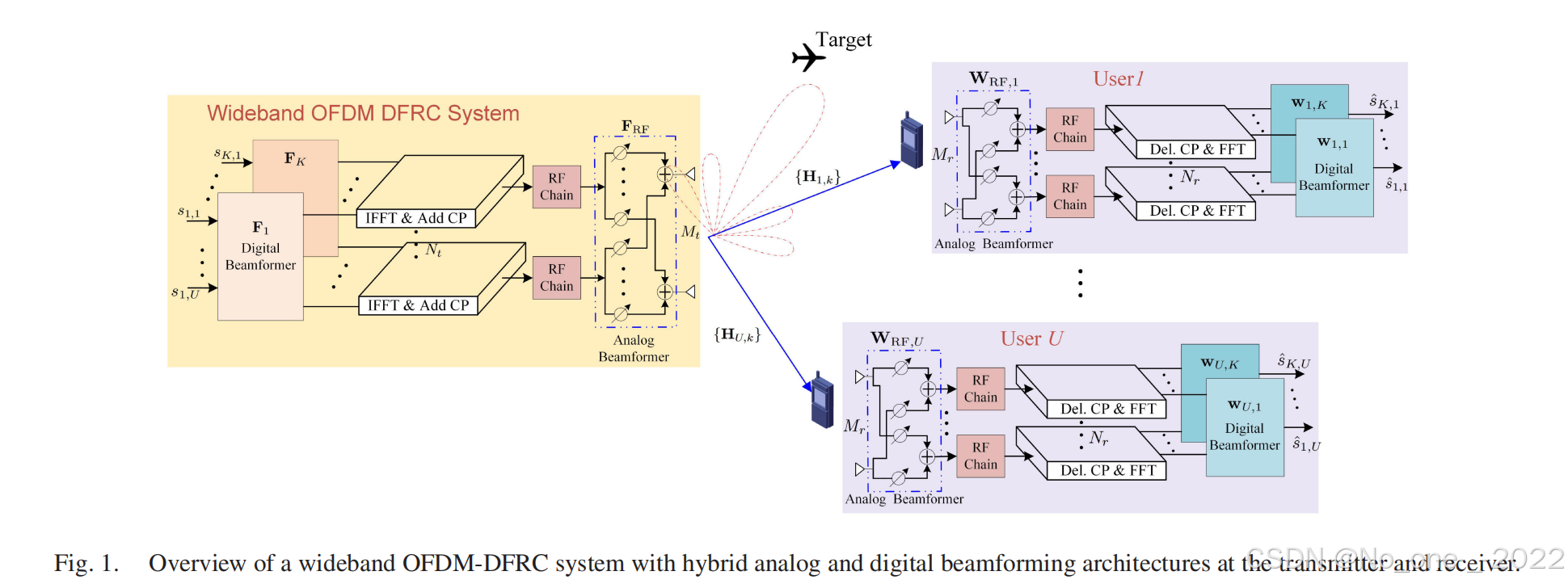
如图1所示，我们考虑一个宽带 OFDM-DFRC 系统，该系统同时向多个用户发送通信符号，并向感兴趣的目标发射雷达探测波形。发射机配有$N_t$条射频链和$M_t$根天线，服务于$U$个用户，每个用户都配备了$N_r$条射频链和$M_r$根天线。数据符号经过调制并扩展到$K$个子载波上。我们假设射频链的数量$N_t$小于发射天线的数量$M_t$，并且每个子载波的用户数$U$小于或等于$N_t$，即$U\le N_t<M_t$。发射机和用户都配备了均匀线性阵列（ULAs），阵元间距为$\delta$。

数据符号 ${\mathbf{s}}_k$ 首先在频域由数字波束赋形器 ${\mathbf{F}}_k=[f_{k,1},...,f_{k,U}]\in {\mathbb{C}}^{N_t\times U}$ 进行处理，然后利用$N_t$个$K$点快速傅里叶逆变换（IFFT）将符号块转换到时域。接着，在对处理后的信号进行上变频并通过时域的 ${\mathbf{F}}_{\text{RF}}\in {\mathbb{C}}^{M_t\times N_t}$ 执行模拟波束赋形之前，会向信号中添加一个长度为$D$的循环前缀。需要注意的是，射频波束赋形器对所有子载波保持不变。

记 $\Delta t$ 为OFDM符号持续时间，在时刻 $t\in (0,\Delta t]$ 的发射信号可以用向量形式 $\mathbf{x}(t)\in {\mathbb{C}}^{M_t}$表示为

$$\mathbf{x}(t)=\sum _{k=1}^K{\mathbf{F}}_{\text{RF}}{\mathbf{F}}_k{\mathbf{s}}_k{e}^{j2\pi f_{k}t}\text{\hspace{1em}(1)}$$

其中 $f_k=(k-1)\Delta f$，$\Delta f$ 是OFDM信号的频率步长。为了保证子载波的正交性，我们设定$\Delta f=1/\Delta t$。

在本工作中，我们考虑一种全连接的波束赋形配置，其中发射机的每条射频链都通过一组移相器连接到所有天线。因此，${\mathbf{F}}_{\text{RF}}$ 的每个元素都具有单位模值，即 $|{\mathbf{F}}_{\text{RF}}(i,j)|=1,\forall i,j$。此外，我们假设每个子载波上的发射机功率满足以下条件：

$${\Vert {\mathbf{F}}_{\mathrm{RF}}{\mathbf{F}}_k\Vert }_F^2={\mathcal{P}}_k\text{\hspace{1em}(2)}$$

在此，我们将专注于具有无限分辨率移相器的混合波束赋形设计。对于有限分辨率的情况也将进行简要讨论。

B. Communication Model

将从发射机到用户 $u$ 在子载波$k$上的信道状态信息（CSI）矩阵表示为 ${\mathbf{H}}_{k,u}\in {\mathbb{C}}^{M_r\times M_t}$，并采用几何宽带信道模型（geometric wideband channel model）（例如，见[29], [38], [43]和[44]）。需要注意的是，在RCSS 和 DFRC系统中，CSI的估计非常重要，并且仍然是一个悬而未决的问题[24], [45]。在本工作中，我们假设它是已知的。用户 $u$ 的接收信号可以表示为

$${\mathbf{r}}_{k,u}(t)={\mathbf{H}}_{k,u}{\mathbf{F}}_{\mathrm{RF}}{\mathbf{F}}_k{\mathbf{s}}_k{e}^{ȷ2\pi f_{k}t}+{\mathbf{ϵ}}_{k,u}(t)\text{\hspace{1em}(3)}$$

其中${ϵ}_{k,u}(t)$是第$u$个用户在第$k$个子载波上的加性高斯白噪声（AWGN），其均值为零，协方差矩阵为 $\Delta t{\sigma }_{ϵ}^2{I}_{M_r}$。

第 $u$ 个用户的接收信号首先由一个通过模拟移相器实现的射频波束赋形器 ${\mathbf{W}}_{RF,u}\in {\mathbb{C}}^{M_r\times N_r}$进行处理，即 ${\mathbf{W}}_{RF,u}(i,j)=e^{j{\Phi }_{i,j}},i=1,...,M_r;j=1,...,N_r$。接下来，删除循环前缀，并使用$N_r$ 个$K$点FFT将信号转换到频域。在每个子载波$k$上，应用一个数字合并器（digital combiner） ${\mathbf{w}}_{k,u}\in {\mathbb{C}}^{N_r}$来估计第$u$个用户在第$k$个子载波上的符号，如下所示[46], [47]

$$\begin{array}{rl}{\hat{s}}_{k,u}& ={\mathbf{w}}_{k,u}^H{\mathbf{W}}_{\mathrm{RF},u}^H{\mathbf{H}}_{k,u}{\mathbf{F}}_{\mathrm{RF}}{\mathbf{F}}_k{\mathbf{s}}_k+{\mathbf{w}}_{k,u}^H{\mathbf{W}}_{\mathrm{RF},u}^H{\mathbf{v}}_{k,u}\\ & =\underset{\text{desired signal }}{\underbrace{{\mathbf{w}}_{k,u}^H{\mathbf{W}}_{\mathrm{RF},u}^H{\mathbf{H}}_{k,u}{\mathbf{F}}_{\mathrm{RF}}{\mathbf{f}}_{k,u}{s}_{k,u}}}\\ & +\underset{\text{multi-user interference (MUI) }}{\underbrace{\sum _{i\ne u}^U{\mathbf{w}}_{k,u}^H{\mathbf{W}}_{\mathrm{RF},u}^H{\mathbf{H}}_{k,u}{\mathbf{F}}_{\mathrm{RF}}{\mathbf{f}}_{k,i}{s}_{k,i}}}+{\mathbf{w}}_{k,u}^H{\mathbf{W}}_{\mathrm{RF},u}{\mathbf{v}}_{k,u}\end{array}\text{\hspace{1em}(4)}$$

其中第一项表示期望信号，而第二项表示不想要的多用户干扰（MUI）。$v_{k,u}=\frac{1}{\Delta t}{\int }_0^{\Delta t}{ϵ}_{k,u}(t)e^{-j2\pi f_{k}t}dt$表示加性噪声，其均值为零，方差矩阵为${\sigma }_{ϵ}^2{I}_{M_r}$，并假设其与$s_k$无关。

为简化符号，我们定义

$$\begin{array}{rl}{\mathbf{u}}_{k,u}& ={\mathbf{W}}_{\text{RF},u}{\mathbf{w}}_{k,u}\in {\mathbb{C}}^{M_r}\\ {\mathbf{p}}_{k,u}& ={\mathbf{F}}_{\text{RF}}{\mathbf{f}}_{k,u}\in {\mathbb{C}}^{M_t}\end{array}\text{\hspace{1em}(5)}$$

那么，均方估计误差（MSE）$e_{k,u}$可以写为

$$\begin{array}{rl}{e}_{k,u}& \triangleq {\mathbb{E}}_{{\mathbf{s}}_{k,u},{\mathbf{v}}_k}\left[({\hat{s}}_{k,u}-s_{k,u})({\hat{s}}_{k,u}-s_{k,u}{)}^H\right]\\ & =|{\mathbf{u}}_{k,u}^H{\mathbf{H}}_{k,u}{\mathbf{p}}_{k,u}-1{|}^2\\ & +\sum _{i\ne u}^U|{\mathbf{u}}_{k,u}^H{\mathbf{H}}_{k,u}{\mathbf{p}}_{k,i}{|}^2+{\sigma }_{ϵ}^2{\mathbf{u}}_{k,u}^H{\mathbf{u}}_{k,u}\end{array}\text{\hspace{1em}(6)}$$

对于一个固定的发射波束赋形器，根据[48]，我们可知MMSE接收机由下式给出

$${\mathbf{u}}_{k,u}^{\text{MMSE}}={\left({\mathbf{H}}_{k,u}{\mathbf{F}}_{\text{RF}}{\mathbf{F}}_k{\mathbf{F}}_k^H{\mathbf{F}}_{\text{RF}}^H{\mathbf{H}}_{k,u}^H+{\sigma }_{ϵ}^2{\mathbf{I}}_{M_r}\right)}^{-1}{\mathbf{H}}_{k,u}{\mathbf{p}}_{k,u}\text{\hspace{1em}(7)}$$