算法第四十六天：动态规划part13（第九章）

1.回文子串

📌 核心思路

1. 定义 dp[i][j]：表示子串 s[i..j] 是否为回文。

2. 状态转移：

   • 情况一：单个字符必然是回文 → j == i

   • 情况二：两个字符相等 → s[i] == s[j] 且 j - i == 1

   • 情况三：长度大于 2 时 → s[i] == s[j] and dp[i+1][j-1] == True

3. 遍历顺序：i 从右往左，j 从左往右，保证计算 dp[i+1][j-1] 时已经有结果。

class Solution:def countSubstrings(self, s: str) -> int:#dp[i][j]是表示s[i, j]是否是回文字串#初始化dp = [[False] * len(s) for _ in range(len(s))]count = 0#递归公式for i in range(len(s)-1, -1, -1):for j in range(i, len(s)):if s[i] == s[j]:if j-i <= 1: #情况1和2count += 1dp[i][j] = Trueelif dp[i+1][j-1]:#情况3：长度大于2count += 1dp[i][j] = Truereturn count

2.最长回文子序列

📝 最长回文子序列（LPS）思路总结

1. 问题定义

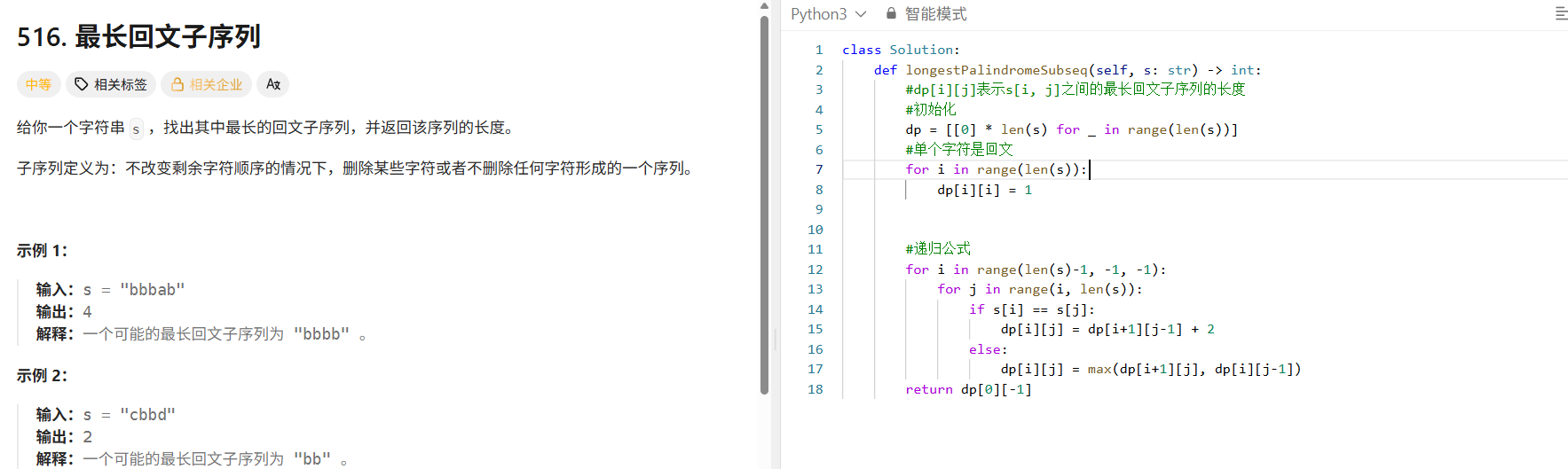
给定字符串 s，求其中的 最长回文子序列（subsequence）的长度。
⚠️ 注意：子序列可以不连续，但必须保持原有顺序；和 子串（substring） 不同。

---

2. 动态规划状态定义

设二维数组：

dp[i][j]=字符串 s[i..j] 的最长回文子序列长度dp[i][j] = \text{字符串 } s[i..j] \text{ 的最长回文子序列长度}dp[i][j]=字符串 s[i..j] 的最长回文子序列长度

---

3. 状态转移方程

1. 如果 s[i] == s[j]：

   • 当 i == j：只有一个字符，dp[i][j] = 1

   • 当 j == i+1：两个字符相等，dp[i][j] = 2

   • 一般情况：

     dp[i][j]=dp[i+1][j−1]+2dp[i][j] = dp[i+1][j-1] + 2dp[i][j]=dp[i+1][j−1]+2

2. 如果 s[i] != s[j]：

   dp[i][j]=max⁡(dp[i+1][j],dp[i][j−1])dp[i][j] = \max(dp[i+1][j], dp[i][j-1])dp[i][j]=max(dp[i+1][j],dp[i][j−1])

---

4. 边界条件

• 单个字符：

  dp[i][i]=1dp[i][i] = 1dp[i][i]=1

---

5. 遍历顺序

• 因为 dp[i][j] 依赖 dp[i+1][j-1]、dp[i+1][j]、dp[i][j-1]，所以必须 从右往左枚举 i，从左往右枚举 j。

---

6. 答案

最终答案是：

dp[0][n−1]dp[0][n-1]dp[0][n−1]

即整个字符串的最长回文子序列长度。

class Solution:def longestPalindromeSubseq(self, s: str) -> int:#dp[i][j]表示s[i, j]之间的最长回文子序列的长度#初始化dp = [[0] * len(s) for _ in range(len(s))]#单个字符是回文for i in range(len(s)):dp[i][i] = 1#递归公式for i in range(len(s)-1, -1, -1):for j in range(i+1, len(s)):if s[i] == s[j]:if j == i+1:dp[i][j] = 2else: dp[i][j] = dp[i+1][j-1] + 2else:dp[i][j] = max(dp[i+1][j], dp[i][j-1])return dp[0][-1]

动态规划终于结束了！！！撒花儿~

总结如下：代码随想录