洛谷P1595讲解（加强版）+错排讲解

前言

接我原先的文章，因为一场考试，让我对这道题记忆深刻

注：（因为那道题，所以80分）

正文

1.分析题目

题目：

某人写了 n 封信和 n 个信封，如果所有的信都装错了信封。求所有信都装错信封共有多少种不同情况。

输入格式

一个信封数 n，保证 n≤20。

输出格式

一个整数，代表有多少种情况。

考虑特殊情况，若信封数为0，则一种，若信封数位两，则1种。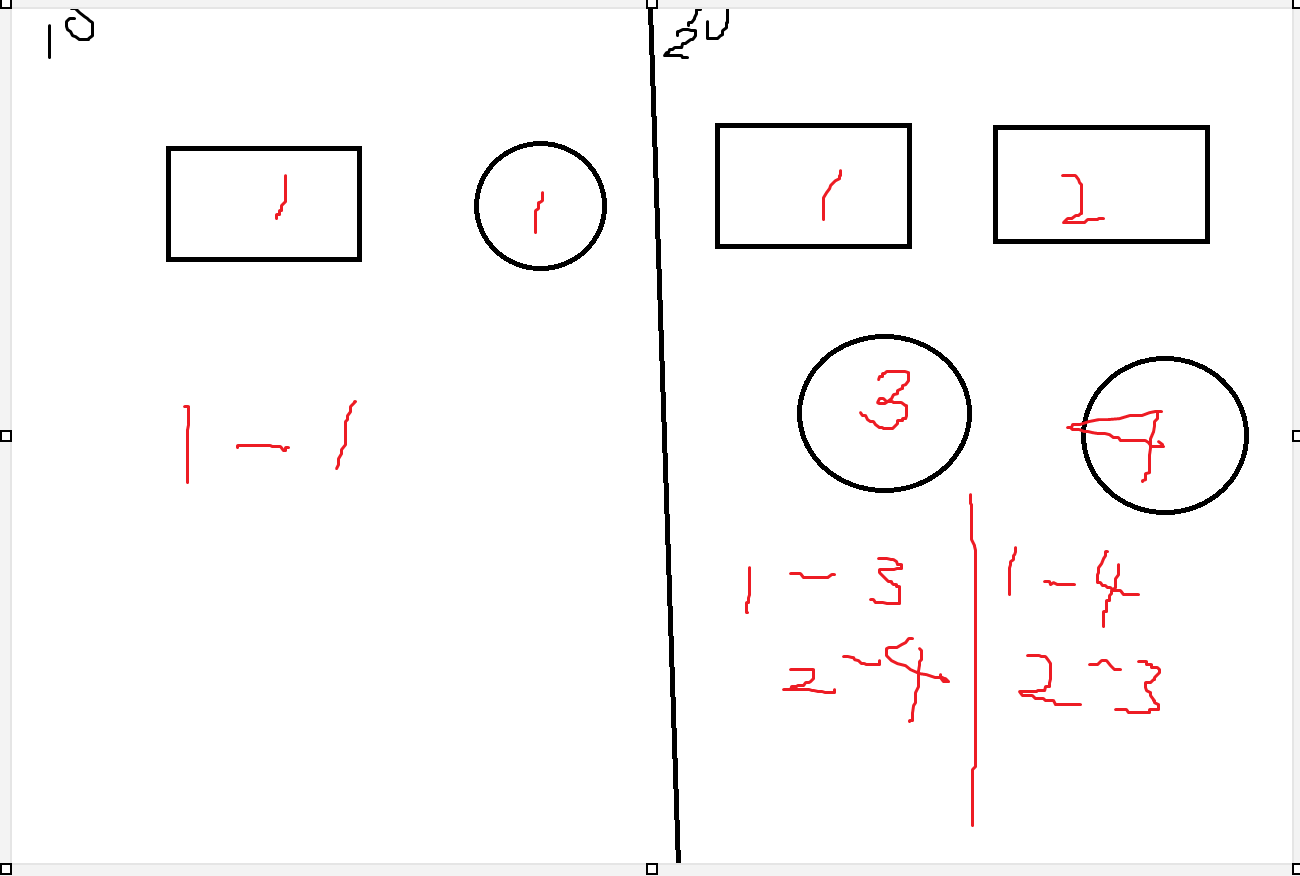

可以构造函数：

def g(n):if n==1:return 0if n==2:return 1

若大于二，则使用错排问题）

错排问题

错排问题概述

错排问题（Derangement Problem）是组合数学中的一个经典问题，指在排列中没有任何一个元素出现在其原始位置的情况。具体来说，给定n个元素，求所有排列中满足“没有元素在初始位置”的排列数，记为D(n)。

错排公式推导

错排数D(n)可以通过递推公式或显式公式计算：

递推公式： [ D(n) = (n-1) \times (D(n-1) + D(n-2)) ] 初始条件： [ D(1) = 0 ] [ D(2) = 1 ]

显式公式： [ D(n) = n! \times \left(1 - \frac{1}{1!} + \frac{1}{2!} - \frac{1}{3!} + \dots + (-1)^n \frac{1}{n!}\right) ] 或简化为： [ D(n) = \left\lfloor \frac{n!}{e} + \frac{1}{2} \right\rfloor ] 其中e是自然对数的底数（约2.71828），⌊·⌋表示取整函数。

错排问题的实现代码

以下是错排数的两种实现方式：递归和动态规划。

递归实现

def derangement_recursive(n):if n == 1:return 0if n == 2:return 1return (n - 1) * (derangement_recursive(n - 1) + derangement_recursive(n - 2))

动态规划实现

def derangement_dp(n):if n == 1:return 0if n == 2:return 1dp = [0] * (n + 1)dp[1], dp[2] = 0, 1for i in range(3, n + 1):dp[i] = (i - 1) * (dp[i - 1] + dp[i - 2])return dp[n]

错排问题的应用

错排问题在实际中有多种应用，例如：

• 密码学中用于生成无固定点的排列。
• 概率论中用于计算“完全混乱”的概率。
• 算法设计中用于某些排列相关的优化问题。

示例

计算n=4时的错排数：

• 显式公式计算： [ D(4) = 4! \times \left(1 - \frac{1}{1!} + \frac{1}{2!} - \frac{1}{3!} + \frac{1}{4!}\right) = 24 \times \left(1 - 1 + 0.5 - 0.1667 + 0.0417\right) = 9 ]
• 递推公式计算： [ D(4) = 3 \times (D(3) + D(2)) = 3 \times (2 + 1) = 9 ]

两种方法结果一致。

固有错排公式（n-1）*(g(n-1)+g(n-2))

完整代码

def xf(n):if n==1:return 0if n==2:return 1if n>2:return (n-1)*(xf(n-1)+xf(n-2))
n=int(input())
print(xf(n))

感谢大家点赞收藏！！！