力扣(接雨水)——标准双指针
剖析 LeetCode 42. 接雨水:双指针的高效解题思路
一、题目剖析
(一)问题描述
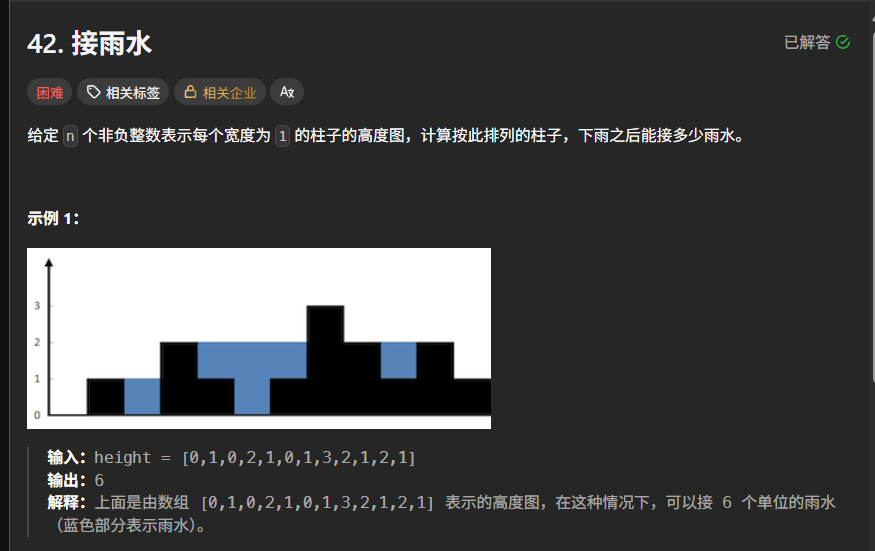
给定表示柱子高度的非负整数数组 height,计算下雨后这些柱子能承接的雨水总量。雨水能留存的关键在于形成“凹槽”,即左右两侧有更高的柱子,中间柱子较低,从而储存雨水。
(二)核心挑战
- 边界确定:需找到每个位置左右两侧的最高柱子,以此确定该位置能承接雨水的高度上限。
- 高效计算:避免对每个位置都单独遍历寻找左右最高柱(暴力法时间复杂度高 ),需借助双指针,在一次遍历中同时维护左右边界信息。
- 逻辑推导:理解雨水高度由左右边界的较低高度决定,宽度为 1(每个柱子宽度固定为 1 ),通过指针移动动态计算每个位置的储水量。
二、算法思想:双指针的巧妙运用
(一)双指针的作用
使用左右双指针(left 从数组开头出发,right 从数组末尾出发 ),用于:
- 维护左右边界高度:
leftMax记录left指针遍历过的最高柱子高度,rightMax记录right指针遍历过的最高柱子高度。 - 动态计算储水量:根据左右指针对应的柱子高度,决定移动哪一侧指针。若
height[left] < height[right],移动left指针;反之移动right指针。每次移动后,判断当前指针位置的柱子高度与对应边界高度的关系,计算储水量或更新边界高度。
(二)指针移动与储水计算逻辑
- 指针移动规则:始终移动当前指针中,对应柱子高度较低的一侧。例如
height[left] < height[right]时,移动left指针,因为此时右侧有更高的柱子,左侧的储水情况由leftMax决定。 - 储水量计算:当移动指针后,若当前柱子高度小于对应边界高度(
leftMax或rightMax),说明该位置可储水,储水量为边界高度与当前柱子高度的差值;若当前柱子高度大于等于边界高度,更新边界高度为当前柱子高度。
三、代码实现与深度解析
//标准双指针
class Solution {public int trap(int[] height) {// 边界条件:数组长度<3时,无法形成凹槽储水if (height == null || height.length < 3) {return 0;}int sumRain = 0;//定义左右指针int left = 0;int right = height.length - 1;//定义左边界和右边界(找当前遍历过元素的最大值)int leftMax = height[0];int rightMax = height[height.length - 1];//循环条件为,左右指针不相遇while (left < right) {//移动指针//移动条件为左右指针的那个值小移动哪一个if (height[left] < height[right]) //左指针{left++;//判断移动指针后的值,是否大于当前的左边界//大于的话更新左边界,小于则计算雨水if (height[left] < leftMax) {sumRain +=leftMax- height[left];} else {leftMax = height[left];}} else { //右指针right--;//判断移动指针后的值,是否大于当前的右边界//大于的话更新右边界,小于则计算雨水if (height[right] < rightMax) {sumRain +=rightMax- height[right] ;} else {rightMax = height[right];}}}return sumRain;}
}
(一)代码执行流程
- 边界处理:若数组
height为null或长度小于 3,直接返回0(无法形成凹槽储水 )。 - 初始化变量:
sumRain初始化为0(总储水量 ),left指向数组起始位置(0),right指向数组末尾位置(height.length - 1),leftMax初始为height[0],rightMax初始为height[height.length - 1]。 - 双指针遍历:进入
while循环,只要left < right,持续执行:- 比较
height[left]和height[right]:- 若
height[left] < height[right],移动left指针:- 若
height[left] < leftMax,说明该位置可储水,储水量为leftMax - height[left],累加到sumRain。 - 若
height[left] >= leftMax,更新leftMax为height[left]。
- 若
- 反之,移动
right指针:- 若
height[right] < rightMax,储水量为rightMax - height[right],累加到sumRain。 - 若
height[right] >= rightMax,更新rightMax为height[right]。
- 若
- 若
- 比较
- 返回结果:循环结束后,
sumRain即为总接雨水量,返回该值。
(二)关键逻辑拆解
- 边界条件判断:数组长度小于 3 时,无法形成至少两个高柱子夹一个低柱子的凹槽,直接返回
0,避免无效计算。 - 指针移动与储水判断:通过比较左右指针对应柱子高度,决定移动方向,确保每次处理的是当前“可储水潜力更大”的一侧。移动后,根据当前柱子高度与边界高度的关系,计算储水量或更新边界,充分利用双指针维护的边界信息。
- 储水量计算:雨水高度由左右边界的较低高度决定,但在双指针法中,通过维护
leftMax和rightMax,动态判断当前位置的储水能力,将时间复杂度优化到O(n)(仅需一次遍历 )。
四、复杂度分析
(一)时间复杂度
双指针只需遍历一次数组(left 和 right 从两端向中间移动,每个元素最多被访问一次 ),时间复杂度为 O(n) ,n 为数组 height 的长度。
(二)空间复杂度
代码中仅使用常数级别的额外变量(sumRain、left、right、leftMax、rightMax ),空间复杂度为 O(1) 。
