[Pyro概率编程] 推理算法Infer | 随机变分推断SVI | MCMC采样机制
第六章:推理算法(Infer)
欢迎回来(。・∀・)
通过前几章的学习,我们已经对于 参数空间 我们了解了:
- 第一章:基础构件 介绍了可学习参数
pyro.param - 第三章:参数存储库 解析了参数管理机制
- 第五章:优化器 揭示了参数调整的核心算法
但优化器如同需要训练计划的教练,必须明确优化目标与评估方式。推理算法正是为此而生,它们为优化过程提供系统性解决方案!
核心理念
假设我们构建了一个描述数据生成机制的复杂概率模型(“配方”),其中包含未知参数或隐变量(“秘制调料”)。我们已收集实际观测数据(“成品菜肴”),需要逆向推导最优参数组合。
推理算法就是完成这一逆向工程的"主厨",通过协调模型、数据与优化器,系统性地探索参数空间以找到最优解。
Pyro提供两大核心推理方法:
-
随机变分推断(
SVI)
通过迭代优化近似后验分布的参数,快速寻找近似最优解 -
马尔可夫链蒙特卡洛(
MCMC)
通过系统采样探索参数空间,获取精确后验分布(计算成本较高)
关键组件
推理算法整合以下核心元素:
模型(Model):描述数据与隐变量关系的概率程序引导函数(Guide,仅SVI):近似隐变量后验分布的简化模型观测数据:用于逆向推导的实际观测结果损失函数:衡量当前参数拟合程度的量化指标优化器:执行参数更新的优化算法
随机变分推断(SVI)实践
SVI将学习问题转化为优化问题,通过最小化证据下界(ELBO)实现高效推理:
实施步骤
- 定义概率模型:完整描述数据生成过程
- 构建引导函数:声明可学习参数,匹配模型隐变量结构
- 选择优化器:如
Adam,配置学习率等超参数 - 指定损失函数:常用
Trace_ELBO - 实例化SVI对象:整合模型、引导函数、优化器与损失函数
- 执行训练循环:迭代调用
step()更新参数
以硬币偏置学习为例(10次投掷观测到8次正面):
import pyro
import pyro.distributions as dist
import pyro.optim as optim
from pyro.infer import SVI, Trace_ELBO
import torch# 观测数据(8次正面,2次反面)
observed_data = torch.tensor([1.0, 1.0, 0.0, 1.0, 1.0, 1.0, 0.0, 1.0, 1.0, 1.0])# 1. 定义生成模型
def coin_model(data):p = pyro.sample("p", dist.Beta(1.0, 1.0)) # 均匀先验with pyro.plate("data_loop", len(data)):pyro.sample("obs", dist.Bernoulli(p), obs=data)# 2. 构建引导函数
def coin_guide(data):alpha = pyro.param("guide_alpha", torch.tensor(1.0), constraint=dist.constraints.positive)beta = pyro.param("guide_beta", torch.tensor(1.0),constraint=dist.constraints.positive)pyro.sample("p", dist.Beta(alpha, beta))# 初始化环境
pyro.clear_param_store()
adam = optim.Adam({"lr": 0.01})
elbo = Trace_ELBO()
svi = SVI(coin_model, coin_guide, adam, elbo)# 执行训练
for i in range(1000):loss = svi.step(observed_data)if i % 100 == 0:print(f"Iter {i}, Loss: {loss:.2f}")# 输出学习结果
alpha_learned = pyro.param("guide_alpha").item()
beta_learned = pyro.param("guide_beta").item()
print(f"学习参数: alpha={alpha_learned:.2f}, beta={beta_learned:.2f}")
print(f"推断正面概率: {alpha_learned/(alpha_learned+beta_learned):.2f}") # 预期接近0.8
实现解析:
coin_model定义硬币偏置p的Beta先验及观测数据生成过程coin_guide使用可学习的Beta分布参数alpha和beta近似后验- SVI通过ELBO损失指导参数优化,最终
alpha和beta收敛至近似真实后验的参数
马尔可夫链蒙特卡洛(MCMC)实践
马尔可夫链
马尔可夫链是一种数学模型,描述一个系统的状态变化仅依赖于当前状态,与过去的历史无关。
生活例子:
假设每天的天气只有“晴”或“雨”两种状态,且今天的天气仅由昨天的天气决定:
- 昨天是晴天,今天有70%概率继续晴,30%概率转雨;
- 昨天是雨天,今天有50%概率继续雨,50%概率转晴。
这种“明天的天气只取决于今天”的特性就是马尔可夫链的核心。
MCMC通过马尔可夫链采样直接获取后验分布样本,无需引导函数:
实施步骤
- 定义概率模型:同SVI的定义方式
- 选择MCMC核:如NUTS(No-U-Turn Sampler)算法
- 配置MCMC参数:采样次数、预热步数等
- 执行采样过程:运行
run()方法获取后验样本 - 分析采样结果:计算统计量评估后验分布
延续硬币偏置案例:
from pyro.infer import MCMC, NUTS# 定义生成模型(同SVI案例)
def coin_model_mcmc(data):p = pyro.sample("p", dist.Beta(1.0, 1.0))with pyro.plate("data_loop", len(data)):pyro.sample("obs", dist.Bernoulli(p), obs=data)# 执行MCMC采样
pyro.clear_param_store()
nuts_kernel = NUTS(coin_model_mcmc)
mcmc = MCMC(nuts_kernel, num_samples=1000, warmup_steps=500)
mcmc.run(observed_data)# 获取后验样本
mcmc_samples = mcmc.get_samples()
p_posterior = mcmc_samples["p"]
print(f"后验均值: {p_posterior.mean().item():.2f}")
print(f"后验标准差: {p_posterior.std().item():.2f}")
实现解析:
- NUTS算法通过哈密顿动力学高效探索参数空间
- 经过500步预热使马尔可夫链收敛,后续1000步采样获取稳定后验分布
- 样本统计量显示
p的估计值及其不确定性
SVI与MCMC对比指南
| 特性 | SVI | MCMC |
|---|---|---|
| 输出形式 | 近似分布的参数 | 后验分布的真实样本 |
| 计算效率 | 适合大规模数据与复杂模型 | 高维模型计算成本较高 |
| 引导函数需求 | 必需 | 无需 |
| 实时性 | 支持在线学习 | 通常需要完整数据集 |
| 精度 | 依赖引导函数近似能力 | 渐进精确 |
| 典型应用 | 神经网络结合概率模型 | 小数据精确推断 |
底层实现解析
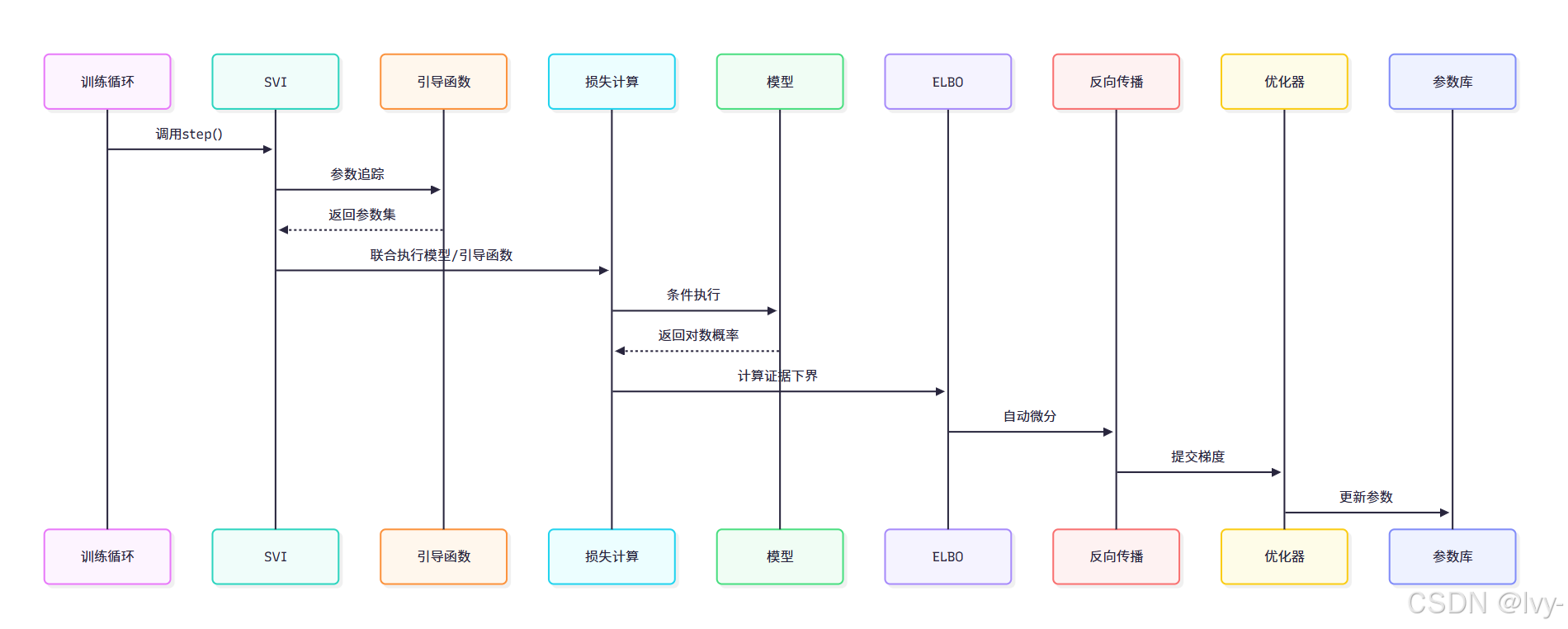
SVI工作流程
- 引导函数追踪:记录可学习参数
- 联合执行模型:通过Poutine效果处理器计算模型与引导函数的对数概率
- ELBO计算:构建证据下界作为损失函数
- 反向传播:计算参数梯度
- 优化器更新:调用PyroOptim更新参数存储库
MCMC采样机制
- 预热阶段:调整采样步长等参数使链收敛
- 采样阶段:基于哈密顿动力学提案,按Metropolis-Hastings准则接受/拒绝
- 样本收集:存储通过检验的参数值构建后验分布
# 简化MCMC核心逻辑
for _ in range(预热步数):生成参数提案计算接受概率按概率接受/拒绝提案for _ in range(采样步数):生成新提案计算接受概率收集接受样本
总结
本章解析了Pyro两大推理范式:
- SVI:通过变分近似实现高效参数学习,适合与深度学习架构整合
- MCMC:通过精确采样获取后验分布,适合小规模精确推断
后续章节将探讨如何通过PyroModule将概率模型与PyTorch模块无缝结合,构建更复杂的混合架构。
