从理论到实战:KNN 算法与鸢尾花分类全解析
数据科学领域,KNN 算法以其简洁直观的特性占据重要地位。本文围绕 KNN 算法的理论基础、实战应用展开深入探讨,通过鸢尾花分类案例实现从理论到实践的完整落地。
KNN 算法核心理论梳理
KNN(K-Nearest Neighbors,K 近邻)算法作为经典的基于距离的分类模型,其核心思想堪称 "物以类聚" 的算法实现。该算法通过计算新数据点与所有已知数据点的距离,选取距离最近的 K 个邻居,最终以这 K 个邻居中占比最高的类别作为新数据点的预测结果,即遵循 "少数服从多数" 的投票原则。
K 值作为关键超参数,需人工手动设置,其取值直接决定模型性能:K 值过小时,模型易受噪声数据影响导致过拟合;K 值过大时,较远的无关样本会干扰预测结果,可能引发欠拟合问题。
算法执行流程清晰明确:首先计算新数据点与所有已知样本的距离(常用欧式距离或曼哈顿距离);接着按距离从小到大排序,选取前 K 个样本作为近邻;最后统计 K 个近邻的类别标签,将出现频率最高的类别确定为预测结果
距离度量方法各有适用场景:
欧式距离计算两点间的直线距离,公式为√(Σ(x₁-x₂)² + (y₁-y₂)²),适用于多维空间的连续特征场景;
曼哈顿距离则计算横平竖直路径的距离总和,公式为 Σ|x₁-x₂| + |y₁-y₂|,在网格状路径场景(如城市道路导航距离计算)中更为适用。
鸢尾花分类实战全流程
以经典的鸢尾花数据集为例,完整演示 KNN 算法的实战应用过程。
首先使用 sklearn 库的 load_iris () 函数加载数据集,其中 data 属性存储花萼长度、花萼宽度、花瓣长度、花瓣宽度等特征数据,target 属性对应鸢尾花的类别标签。
数据划分环节采用 train_test_split 函数,按 7:3 比例将数据集分为训练集(占 70%)和测试集(占 30%),确保模型训练与评估的客观性。模型构建阶段创建 KNeighborsClassifier 分类器,初始设置 K=5,采用欧式距离作为度量方式。

训练过程通过调用 fit 方法实现,将训练集特征(X_train)与标签(y_train)输入模型完成拟合。评估环节使用 score 方法分别计算训练的准确率。

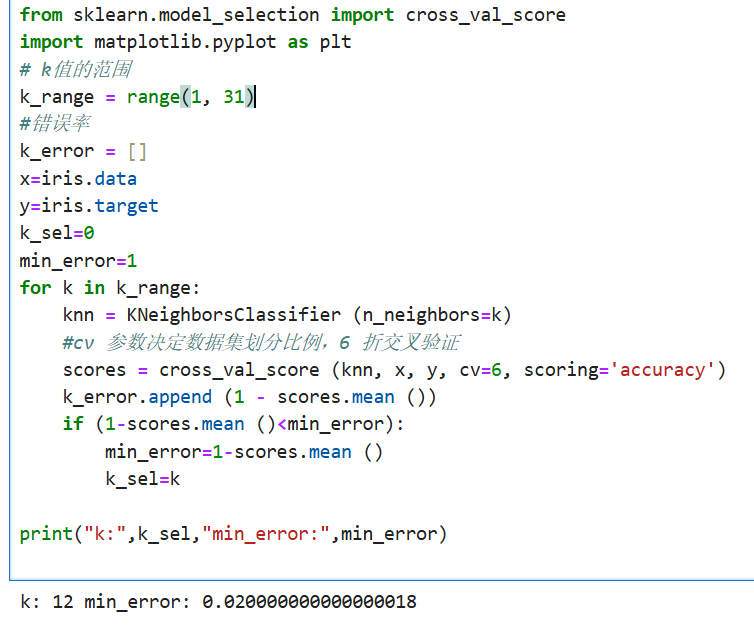
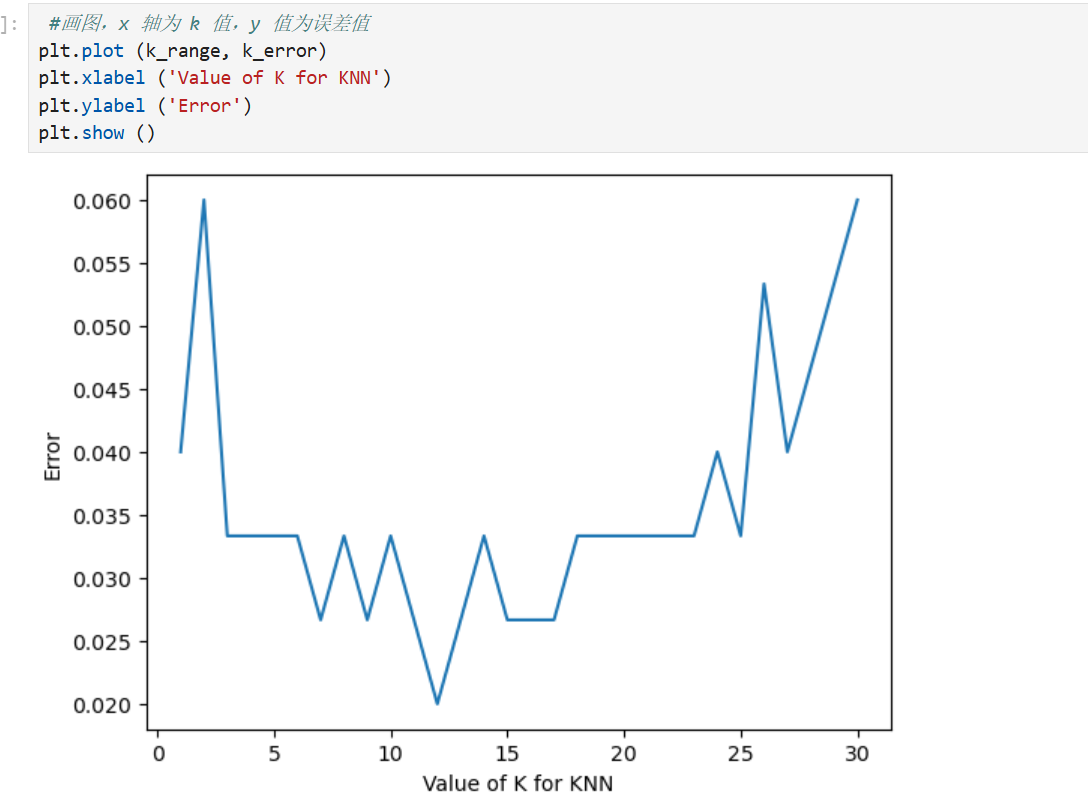
选择合适的k 值
总结
KNN 算法以其简单易懂、实现容易、无需训练过程的特点,成为机器学习入门的绝佳选择。
但 KNN 的能力远不止于此:
在回归任务中,KNN 可通过计算近邻均值实现预测
在异常检测中,可通过判断样本与近邻的距离识别异常点
在推荐系统中,可基于用户的近邻兴趣实现个性化推荐
随着你对机器学习理解的深入,会发现 KNN 虽然简单,却蕴含着 "局部近似" 的深刻思想,这种思想在许多高级算法中都有体现。希望本文能成为你机器学习之旅的良好开端,接下来不妨尝试用 KNN 解决自己感兴趣的问题,相信你会有更多收获!
