归并排序和统计排序

一，归并排序说明

步骤

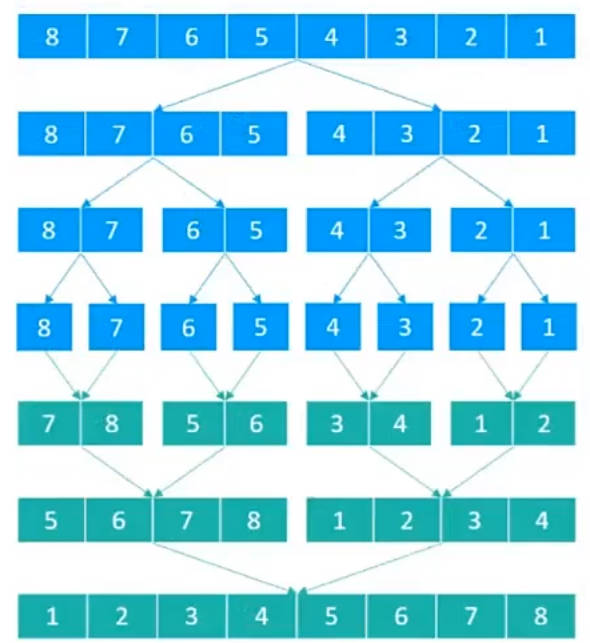
1. 分解阶段：

   • 将数组从中间分成左右两个子数组。

   • 对左右子数组递归地继续分解，直到子数组长度为1（天然有序）。

2. 合并阶段：

   • 比较两个子数组的首元素，将较小的元素放入临时数组。

   • 重复上述过程，直到其中一个子数组被完全合并。

   • 将剩余子数组的元素直接追加到临时数组末尾。

   • 将临时数组拷贝回原数组的对应位置。

二，代码实现

三，计数排序

计数排序是在1954年由Harold H.Seward提出,适合对一定范围内的整数进行排序。

计数排序核心思想：统计每个整数在序列中出现的次数,进而推导出每个整数在有序序列中的索引。 我们以数组[1,4,1,2,5,2,4,1,8]为例进行说明。

第一步:建立一个初始化为0,长度为9 (原始数组中的最大值8加1)的数组count[]

第二步:遍历数组[1,4,1,2,5,2,4,1,8],访问第一个元素1,然后将数组标为1的元素加1,表示当前1出现 了一次，即 count[1] = 1; 依次遍历，对count进行统计。

四，桶排序

桶排序 其实桶排序重要的是它的思想，而不是具体实现，桶排序从字面的意思上看：

1、若干个桶，说明此类排序将数据放入若干个桶中。

2、每个桶有容量，桶是有一定容积的容器，所以每个桶中可能有多个元素。

3、从整体来看，整个排序更希望桶能够更匀称,即既不溢出(太多)又不太少。

假设有一个非整数数列，

如下： 4.5, 0.84, 3.25, 2.18, 0.5

桶排序的第1步，就是创建这些桶，并确定每一个桶的区间范围。

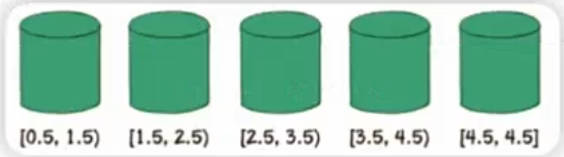
[0.5, 1.5)[1.5, 2.5)[2.5, 3.5)[3.5, 4.5)[4.5, 4.5] 具体需要建立多少个桶，如何确定桶的区间范围，有很多种不同的方式。我们这里创建的桶数量等于原始数列的元素数量,除最后一个桶只包含数列最大值外,前面各个桶的区间按照比例来确定。区间跨度= (最大值-最小值) / (桶的数量-1)

第2步，遍历原始数列，把元素对号入座放入各个桶中。

第3步，对每个桶内部的元素分别进行排序。 第4步，遍历所有的桶，输出所有元素。 0.5, 0.84, 2.18, 3.25, 4.5