线性代数 · 直观理解矩阵 | 空间变换 / 特征值 / 特征向量

注：本文为 “线性代数 · 直观理解矩阵” 相关合辑。
英文引文，机翻未校。
如有内容异常，请看原文。

---

Understanding matrices intuitively, part 1

直观理解矩阵（第一部分）

$3$ March $2011$ William Gould

Introduction to Matrix Visualization

矩阵可视化简介

I want to show you a way of picturing and thinking about matrices. The topic for today is the square matrix, which we will call $\mathbf{A}$. I’m going to show you a way of graphing square matrices, although we will have to limit ourselves to the $2\times 2$ case. That will be, as they say, without loss of generality. The technique I’m about to show you could be used with $3\times 3$ matrices if you had a better $3$-dimensional monitor, and as will be revealed, it could be used on $3\times 2$ and $2\times 3$ matrices, too. If you had more imagination, we could use the technique on $4\times 4$, $5\times 5$, and even higher-dimensional matrices.
我想给大家展示一种想象和思考矩阵的方法。今天的主题是方阵，我们将其称为 $\mathbf{A}$。我会展示一种绘制方阵图形的方法，不过我们得把范围限制在 $2\times 2$ 的情况。正如人们所说，这不会损失一般性。如果有更好的 $3$D 显示器，我要展示的这种方法也适用于 $3\times 3$ 矩阵，而且稍后会发现，它同样适用于 $3\times 2$ 和 $2\times 3$ 矩阵。要是你想象力更丰富些，这种方法还能用于 $4\times 4$、$5\times 5$ 甚至更高维的矩阵。

But we will limit ourselves to $2\times 2$. $\mathbf{A}$ might be
但我们还是先限于 $2\times 2$ 矩阵。$\mathbf{A}$ 可能是

$$\left[\begin{array}{cc}2& 1\\ 1.5& 2\end{array}\right]$$

From now on, I’ll write matrices as
从现在起，我会把矩阵写成这样：

$\mathbf{A}$ = ($2$, $1$ \ $1.5$, $2$)

where commas are used to separate elements on the same row and backslashes are used to separate the rows.
其中，逗号用于分隔同一行的元素，反斜杠用于分隔不同的行。

Transforming Points in Space

空间中的点变换

To graph $\mathbf{A}$, I want you to think about
要绘制 $\mathbf{A}$ 的图形，我希望大家思考这样一个式子：

$\mathbf{y}$ = $\mathbf{Ax}$

where
其中

$\mathbf{y}$: $2\times 1$,

$\mathbf{A}$: $2\times 2$, and

$\mathbf{x}$: $2\times 1$.

That is, we are going to think about $\mathbf{A}$ in terms of its effect in transforming points in space from $\mathbf{x}$ to $\mathbf{y}$. For instance, if we had the point
也就是说，我们要从 $\mathbf{A}$ 将空间中的点从 $\mathbf{x}$ 变换到 $\mathbf{y}$ 的作用这个角度来理解 $\mathbf{A}$。例如，如果我们有这样一个点：

$\mathbf{x}$ = ($0.75$ \ $0.25$)

then

那么

$\mathbf{y}$ = ($1.75$ \ $1.625$)

because by the rules of matrix multiplication $y[1]=0.75\times 2+0.25\times 1=1.75$ and $y[2]=0.75\times 1.5+0.25\times 2=1.625$. The matrix $\mathbf{A}$ transforms the point ($0.75$ \ $0.25$) to ($1.75$ \ $1.625$). We could graph that:
因为根据矩阵乘法规则，$y[1]=0.75\times 2+0.25\times 1=1.75$，$y[2]=0.75\times 1.5+0.25\times 2=1.625$。矩阵 $\mathbf{A}$ 将点 ($0.75$ \ $0.25$) 变换成了 ($1.75$ \ $1.625$)。我们可以把这个过程画出来：

Visualizing Matrix Transformations

可视化矩阵变换

To get a better understanding of how $\mathbf{A}$ transforms the space, we could graph additional points:
为了更好地理解 $\mathbf{A}$ 是如何变换空间的，我们可以绘制更多的点：

I do not want you to get lost among the individual points which $\mathbf{A}$ could transform, however. To focus better on $\mathbf{A}$, we are going to graph $\mathbf{y}$ = $\mathbf{Ax}$ for all $\mathbf{x}$. To do that, I’m first going to take a grid,
不过，我不希望大家迷失在 $\mathbf{A}$ 所能变换的各个点中。为了更专注于 $\mathbf{A}$，我们要为所有的 $\mathbf{x}$ 绘制 $\mathbf{y}$ = $\mathbf{Ax}$ 的图形。为此，我首先会用一个网格：

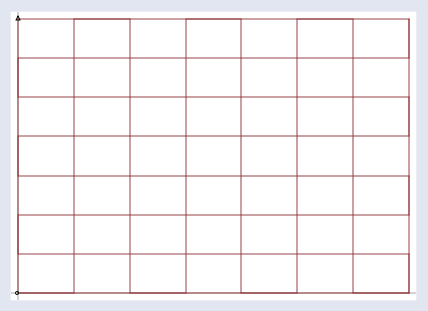
One at a time, I’m going to take every point on the grid, call the point $\mathbf{x}$, and run it through the transform $\mathbf{y}$ = $\mathbf{Ax}$. Then I’m going to graph the transformed points:
我会逐个取出网格上的每个点，将其称为点 $\mathbf{x}$，然后通过变换 $\mathbf{y}$ = $\mathbf{Ax}$ 对其进行处理。接着，我会绘制变换后的点：

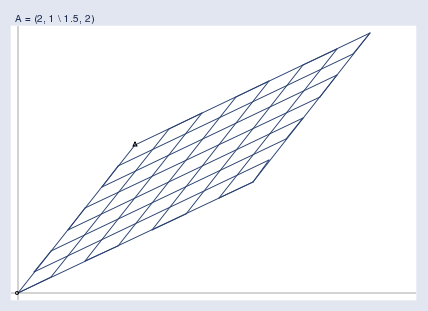
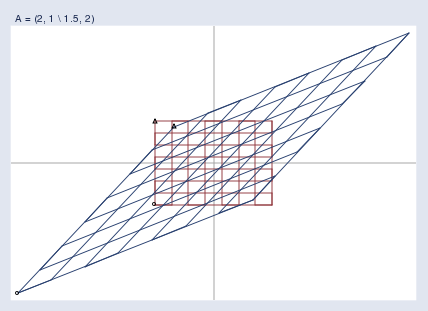
Finally, I’m going to superimpose the two graphs:
最后，我会将这两个图形叠加在一起：

Matrix Effects

矩阵的作用

In this way, I can now see exactly what $\mathbf{A}$ = ($2$, $1$ \ $1.5$, $2$) does. It stretches the space, and skews it.
通过这种方式，我就能清楚地看到 $\mathbf{A}$ = ($2$, $1$ \ $1.5$, $2$) 的作用了。它会拉伸空间，并且使空间发生扭曲。

I want you to think about transforms like $\mathbf{A}$ as transforms of the space, not of the individual points. I used a grid above, but I could just as well have used a picture of the Eiffel tower and, pixel by pixel, transformed it by using $\mathbf{y}$ = $\mathbf{Ax}$. The result would be a distorted version of the original image, just as the the grid above is a distorted version of the original grid. The distorted image might not be helpful in understanding the Eiffel Tower, but it is helpful in understanding the properties of $\mathbf{A}$. So it is with the grids.
我希望大家把像 $\mathbf{A}$ 这样的变换看作是对空间的变换，而不是对单个点的变换。我上面用了网格，但我也完全可以用埃菲尔铁塔的图片，逐个像素地通过 $\mathbf{y}$ = $\mathbf{Ax}$ 进行变换。结果会是原始图像的扭曲版本，就像上面的网格是原始网格的扭曲版本一样。扭曲后的图像可能对理解埃菲尔铁塔没什么帮助，但对理解 $\mathbf{A}$ 的性质却很有帮助。网格的作用也是如此。

Notice that in the above image there are two small triangles and two small circles. I put a triangle and circle at the bottom left and top left of the original grid, and then again at the corresponding points on the transformed grid. They are there to help you orient the transformed grid relative to the original. They wouldn’t be necessary had I transformed a picture of the Eiffel tower.
注意到在上面的图像中有两个小三角形和两个小圆圈。我在原始网格的左下和左上位置各放了一个三角形和一个圆圈，然后在变换后的网格的对应位置也放了同样的图形。它们的作用是帮助你确定变换后的网格相对于原始网格的方位。如果我变换的是埃菲尔铁塔的图片，这些标记就没必要了。

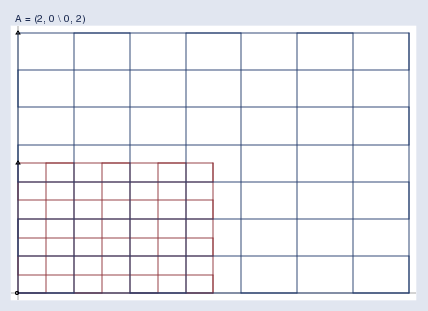
I’ve suppressed the scale information in the graph, but the axes make it obvious that we are looking at the first quadrant in the graph above. I could just as well have transformed a wider area.
我隐藏了图形中的比例尺信息，但从坐标轴可以明显看出，我们看到的是上面图形中的第一象限。我也完全可以变换一个更大的区域。

Matrix Transformations in General

矩阵变换的一般性

Regardless of the region graphed, you are supposed to imagine two infinite planes. I will graph the region that makes it easiest to see the point I wish to make, but you must remember that whatever I’m showing you applies to the entire space.
不管绘制的是哪个区域，你都应该想象成两个无限延伸的平面。我会选择最容易说明我想表达的观点的区域来绘制图形，但你必须记住，我所展示的内容适用于整个空间。

We need first to become familiar with pictures like this, so let’s see some examples. Pure stretching looks like this:
我们首先需要熟悉这样的图形，所以让我们来看一些例子。纯粹的拉伸是这样的：

Pure compression looks like this:
纯粹的压缩是这样的：

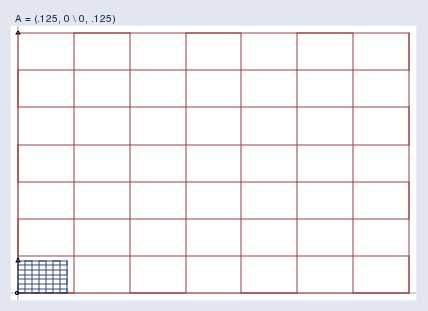
Pay attention to the color of the grids. The original grid, I’m showing in red; the transformed grid is shown in blue.
注意网格的颜色。我把原始网格显示为红色，变换后的网格显示为蓝色。

A pure rotation (and stretching) looks like this:
一个（非纯粹的）旋转（兼拉伸）是这样的：

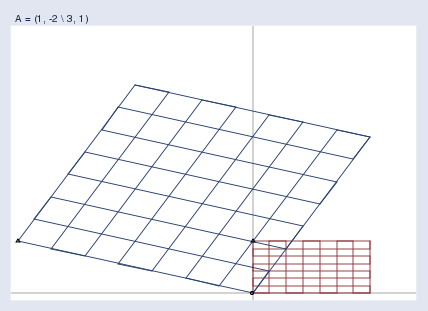
Note the location of the triangle; this space was rotated around the origin.
注意三角形的位置；这个空间是绕原点旋转的。

Here’s an interesting matrix that produces a surprising result: $\mathbf{A}$ = ($1$, $2$ \ $3$, $1$).
有一个有趣的矩阵会产生令人惊讶的结果：$\mathbf{A}$ = ($1$, $2$ \ $3$, $1$)。

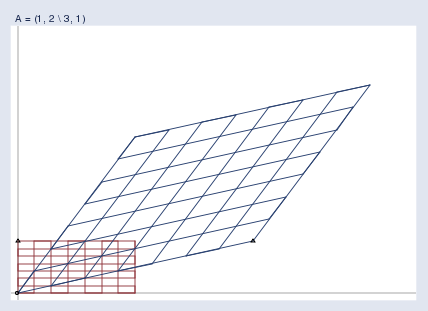
This matrix flips the space! Notice the little triangles. In the original grid, the triangle is located at the top left. In the transformed space, the corresponding triangle ends up at the bottom right! $\mathbf{A}$ = ($1$, $2$ \ $3$, $1$) appears to be an innocuous matrix — it does not even have a negative number in it — and yet somehow, it twisted the space horribly.
这个矩阵会使空间翻转！注意那些小三角形。在原始网格中，三角形位于左上位置。在变换后的空间中，对应的三角形最终出现在右下位置！$\mathbf{A}$ = ($1$, $2$ \ $3$, $1$) 看起来是一个无害的矩阵——里面甚至没有负数——但不知怎的，它把空间扭曲得很厉害。

Singular Matrices

奇异矩阵

So now you know what $2\times 2$ matrices do. They skew, stretch, compress, rotate, and even flip $2$-space. In a like manner, $3\times 3$ matrices do the same to $3$-space; $4\times 4$ matrices, to $4$-space; and so on.
现在你知道 $2\times 2$ 矩阵的作用了。它们会扭曲、拉伸、压缩、旋转甚至翻转二维空间。同样地，$3\times 3$ 矩阵会对三维空间做同样的操作；$4\times 4$ 矩阵会对四维空间做同样的操作，以此类推。

Well, you are no doubt thinking, this is all very entertaining. Not really useful, but entertaining.
毫无疑问，你可能会想，这些都很有趣。虽然没什么实际用处，但挺有意思的。

Okay, tell me what it means for a matrix to be singular. Better yet, I’ll tell you. It means this:
那好，告诉我奇异矩阵是什么意思。更确切地说，我来告诉你。它的意思是这样的：

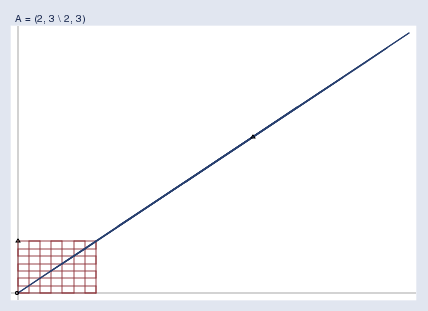
A singular matrix $\mathbf{A}$ compresses the space so much that the poor space is squished until it is nothing more than a line. It is because the space is so squished after transformation by $\mathbf{y}$ = $\mathbf{Ax}$ that one cannot take the resulting $\mathbf{y}$ and get back the original $\mathbf{x}$. Several different $\mathbf{x}$ values get squished into that same value of $\mathbf{y}$. Actually, an infinite number do, and we don’t know which you started with.
奇异矩阵 $\mathbf{A}$ 会极大地压缩空间，把原本的空间挤压成一条线。正是因为经过 $\mathbf{y}$ = $\mathbf{Ax}$ 变换后空间被挤压得如此厉害，所以我们无法根据得到的 $\mathbf{y}$ 反推出原始的 $\mathbf{x}$。多个不同的 $\mathbf{x}$ 值会被挤压成同一个 $\mathbf{y}$ 值。实际上，有无穷多个 $\mathbf{x}$ 值会这样，我们不知道你最初用的是哪一个。

$\mathbf{A}$ = ($2$, $3$ \ $2$, $3$) squished the space down to a line. The matrix $\mathbf{A}$ = ($0$, $0$ \ $0$, $0$) would squish the space down to a point, namely ($0$ $0$). In higher dimensions, say, $k$, singular matrices can squish space into $k-1$, $k-2$, …, or $0$ dimensions. The number of dimensions is called the rank of the matrix.
$\mathbf{A}$ = ($2$, $3$ \ $2$, $3$) 会把空间压缩成一条线。矩阵 $\mathbf{A}$ = ($0$, $0$ \ $0$, $0$) 会把空间压缩成一个点，即 ($0$ $0$)。在更高维的空间中，比如 $k$ 维，奇异矩阵可以把空间压缩成 $k-1$ 维、$k-2$ 维……甚至 $0$ 维。这个维度数被称为矩阵的秩。

Nearly Singular Matrices

近奇异矩阵

Singular matrices are an extreme case of nearly singular matrices, which are the bane of my existence here at StataCorp. Here is what it means for a matrix to be nearly singular:
奇异矩阵是近奇异矩阵的极端情况，是我在 StataCorp 工作时最头疼的问题。近奇异矩阵的含义是这样的：

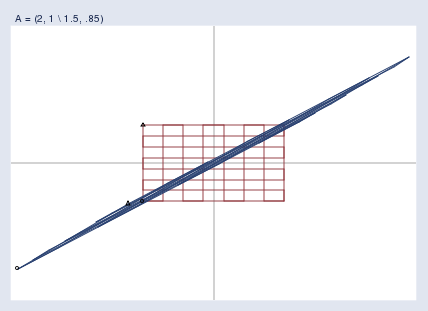
Nearly singular matrices result in spaces that are heavily but not fully compressed. In nearly singular matrices, the mapping from $\mathbf{x}$ to $\mathbf{y}$ is still one-to-one, but $\mathbf{x}$‘s that are far away from each other can end up having nearly equal $\mathbf{y}$ values. Nearly singular matrices cause finite-precision computers difficulty. Calculating $\mathbf{y}$ = $\mathbf{Ax}$ is easy enough, but to calculate the reverse transform $\mathbf{x}$ = ${\mathbf{A}}^{-1}\mathbf{y}$ means taking small differences and blowing them back up, which can be a numeric disaster in the making.
近奇异矩阵会导致空间被严重压缩，但没有完全压缩。对于近奇异矩阵，从 $\mathbf{x}$ 到 $\mathbf{y}$ 的映射仍然是一一对应的，但彼此距离很远的 $\mathbf{x}$ 值最终可能会有几乎相等的 $\mathbf{y}$ 值。近奇异矩阵会给有限精度的计算机带来麻烦。计算 $\mathbf{y}$ = $\mathbf{Ax}$ 还算容易，但计算逆变换 $\mathbf{x}$ = ${\mathbf{A}}^{-1}\mathbf{y}$ 就意味着要处理微小的差异并将其放大，这可能会造成数值计算上的灾难。

Matrix Transformations

矩阵变换

So much for the pictures illustrating that matrices transform and distort space; the message is that they do. This way of thinking can provide intuition and even deep insights. Here’s one:
关于矩阵变换和扭曲空间的图示就说这么多；核心信息是矩阵确实会这样做。这种思考方式能给我们带来直觉，甚至是深刻的见解。比如这样一个见解：

In the above graph of the fully singular matrix, I chose a matrix that not only squished the space but also skewed the space some. I didn’t have to include the skew. Had I chosen matrix $\mathbf{A}$ = ($1$, $0$ \ $0$, $0$), I could have compressed the space down onto the horizontal axis. And with that, we have a picture of nonsquare matrices. I didn’t really need a $2\times 2$ matrix to map $2$-space onto one of its axes; a $2\times 1$ vector would have been sufficient. The implication is that, in a very deep sense, nonsquare matrices are identical to square matrices with zero rows or columns added to make them square. You might remember that; it will serve you well.
在上面完全奇异矩阵的图形中，我选择的矩阵不仅压缩了空间，还使空间产生了一些扭曲。其实我也可以不加入这种扭曲。如果我选择矩阵 $\mathbf{A}$ = ($1$, $0$ \ $0$, $0$)，我可以把空间压缩到水平轴上。由此，我们可以对非方阵有一个认识。我其实并不需要一个 $2\times 2$ 矩阵来将二维空间映射到它的某一个轴上；一个 $2\times 1$ 的向量就足够了。这意味着，从深层次来讲，非方阵等同于通过添加零行或零列使其成为方阵的矩阵。你或许可以记住这一点，它会对你很有帮助。

Here’s another insight:
再来看另一个见解：

In the linear regression formula $\mathbf{b}$ = $({\mathbf{X}}^{\prime }\mathbf{X}{)}^{-1}{\mathbf{X}}^{\prime }\mathbf{y}$, $({\mathbf{X}}^{\prime }\mathbf{X}{)}^{-1}$ is a square matrix, so we can think of it as transforming space. Let’s try to understand it that way.
在线性回归公式 $\mathbf{b}$ = $({\mathbf{X}}^{\prime }\mathbf{X}{)}^{-1}{\mathbf{X}}^{\prime }\mathbf{y}$ 中，$({\mathbf{X}}^{\prime }\mathbf{X}{)}^{-1}$ 是一个方阵，所以我们可以把它看作是对空间的一种变换。让我们试着从这个角度来理解它。

Begin by imagining a case where it just turns out that $({\mathbf{X}}^{\prime }\mathbf{X}{)}^{-1}$ = $\mathbf{I}$. In such a case, $({\mathbf{X}}^{\prime }\mathbf{X}{)}^{-1}$ would have off-diagonal elements equal to zero, and diagonal elements all equal to one. The off-diagonal elements being equal to $0$ means that the variables in the data are uncorrelated; the diagonal elements all being equal to $1$ means that the sum of each squared variable would equal $1$. That would be true if the variables each had mean $0$ and variance $1/N$. Such data may not be common, but I can imagine them.
先设想一种情况：$({\mathbf{X}}^{\prime }\mathbf{X}{)}^{-1}$ = $\mathbf{I}$。在这种情况下，$({\mathbf{X}}^{\prime }\mathbf{X}{)}^{-1}$ 的非对角线元素都为零，对角线元素都为 $1$。非对角线元素为零意味着数据中的变量是不相关的；对角线元素都为 $1$ 意味着每个变量的平方和等于 $1$。如果每个变量的均值为 $0$，方差为 $1/N$，那么情况就是这样。这样的数据可能并不常见，但我可以想象出它们的样子。

If I had data like that, my formula for calculating $\mathbf{b}$ would be $\mathbf{b}$ = $({\mathbf{X}}^{\prime }\mathbf{X}{)}^{-1}{\mathbf{X}}^{\prime }\mathbf{y}$ = $\mathbf{I}{\mathbf{X}}^{\prime }\mathbf{y}$ = ${\mathbf{X}}^{\prime }\mathbf{y}$. When I first realized that, it surprised me because I would have expected the formula to be something like $\mathbf{b}$ = ${\mathbf{X}}^{-1}\mathbf{y}$. I expected that because we are finding a solution to $\mathbf{y}$ = $\mathbf{Xb}$, and $\mathbf{b}$ = ${\mathbf{X}}^{-1}\mathbf{y}$ is an obvious solution. In fact, that’s just what we got, because it turns out that ${\mathbf{X}}^{-1}\mathbf{y}$ = ${\mathbf{X}}^{\prime }\mathbf{y}$ when $({\mathbf{X}}^{\prime }\mathbf{X}{)}^{-1}$ = $\mathbf{I}$. They are equal because $({\mathbf{X}}^{\prime }\mathbf{X}{)}^{-1}$ = $\mathbf{I}$ means that ${\mathbf{X}}^{\prime }\mathbf{X}$ = $\mathbf{I}$, which means that ${\mathbf{X}}^{\prime }$ = ${\mathbf{X}}^{-1}$. For this math to work out, we need a suitable definition of inverse for nonsquare matrices. But they do exist, and in fact, everything you need to work it out is right there in front of you.
如果我有这样的数据，那么计算 $\mathbf{b}$ 的公式就是 $\mathbf{b}$ = $({\mathbf{X}}^{\prime }\mathbf{X}{)}^{-1}{\mathbf{X}}^{\prime }\mathbf{y}$ = $\mathbf{I}{\mathbf{X}}^{\prime }\mathbf{y}$ = ${\mathbf{X}}^{\prime }\mathbf{y}$。当我第一次意识到这一点时，我很惊讶，因为我原本预期公式会是 $\mathbf{b}$ = ${\mathbf{X}}^{-1}\mathbf{y}$ 之类的形式。我之所以会这样预期，是因为我们在求 $\mathbf{y}$ = $\mathbf{Xb}$ 的解，而 $\mathbf{b}$ = ${\mathbf{X}}^{-1}\mathbf{y}$ 是一个显而易见的解。事实上，我们得到的结果正是如此，因为当 $({\mathbf{X}}^{\prime }\mathbf{X}{)}^{-1}$ = $\mathbf{I}$ 时，${\mathbf{X}}^{-1}\mathbf{y}$ = ${\mathbf{X}}^{\prime }\mathbf{y}$。它们相等是因为 $({\mathbf{X}}^{\prime }\mathbf{X}{)}^{-1}$ = $\mathbf{I}$ 意味着 ${\mathbf{X}}^{\prime }\mathbf{X}$ = $\mathbf{I}$，这又意味着 ${\mathbf{X}}^{\prime }$ = ${\mathbf{X}}^{-1}$。要让这个数学推理成立，我们需要一个适用于非方阵的逆矩阵定义。但这样的定义确实存在，而且实际上，你需要的所有用来推导的东西都明摆在眼前。

Anyway, when correlations are zero and variables are appropriately normalized, the linear regression calculation formula reduces to $\mathbf{b}$ = ${\mathbf{X}}^{\prime }\mathbf{y}$. That makes sense to me (now) and yet, it is still a very neat formula. It takes something that is $N\times k$ — the data — and makes $k$ coefficients out of it. ${\mathbf{X}}^{\prime }\mathbf{y}$ is the heart of the linear regression formula.
不管怎样，当变量间的相关性为零且变量经过适当标准化后，线性回归的计算公式就简化为 $\mathbf{b}$ = ${\mathbf{X}}^{\prime }\mathbf{y}$。（现在）这对我来说是有意义的，而且这仍然是一个非常简洁的公式。它接收一个 $N\times k$ 的数据，然后从中得出 $k$ 个系数。${\mathbf{X}}^{\prime }\mathbf{y}$ 是线性回归公式的核心。

Let’s call $\mathbf{b}$ = ${\mathbf{X}}^{\prime }\mathbf{y}$ the naive formula because it is justified only under the assumption that $({\mathbf{X}}^{\prime }\mathbf{X}{)}^{-1}$ = $\mathbf{I}$, and real ${\mathbf{X}}^{\prime }\mathbf{X}$ inverses are not equal to $\mathbf{I}$. $({\mathbf{X}}^{\prime }\mathbf{X}{)}^{-1}$ is a square matrix and, as we have seen, that means it can be interpreted as compressing, expanding, and rotating space. (And even flipping space, although it turns out the positive-definite restriction on ${\mathbf{X}}^{\prime }\mathbf{X}$ rules out the flip.) In the formula $({\mathbf{X}}^{\prime }\mathbf{X}{)}^{-1}{\mathbf{X}}^{\prime }\mathbf{y}$, $({\mathbf{X}}^{\prime }\mathbf{X}{)}^{-1}$ is compressing, expanding, and skewing ${\mathbf{X}}^{\prime }\mathbf{y}$, the naive regression coefficients. Thus $({\mathbf{X}}^{\prime }\mathbf{X}{)}^{-1}$ is the corrective lens that translates the naive coefficients into the coefficient we seek. And that means ${\mathbf{X}}^{\prime }\mathbf{X}$ is the distortion caused by scale of the data and correlations of variables.
我们把 $\mathbf{b}$ = ${\mathbf{X}}^{\prime }\mathbf{y}$ 称为朴素公式，因为它只有在 $({\mathbf{X}}^{\prime }\mathbf{X}{)}^{-1}$ = $\mathbf{I}$ 这一假设下才成立，而实际中 ${\mathbf{X}}^{\prime }\mathbf{X}$ 的逆矩阵并不等于 $\mathbf{I}$。$({\mathbf{X}}^{\prime }\mathbf{X}{)}^{-1}$ 是一个方阵，正如我们所看到的，这意味着它可以被理解为对空间的压缩、扩展和旋转（甚至是翻转，尽管事实证明 ${\mathbf{X}}^{\prime }\mathbf{X}$ 的正定限制排除了翻转的可能）。在公式 $({\mathbf{X}}^{\prime }\mathbf{X}{)}^{-1}{\mathbf{X}}^{\prime }\mathbf{y}$ 中，$({\mathbf{X}}^{\prime }\mathbf{X}{)}^{-1}$ 正在对朴素回归系数 ${\mathbf{X}}^{\prime }\mathbf{y}$ 进行压缩、扩展和扭曲。因此，$({\mathbf{X}}^{\prime }\mathbf{X}{)}^{-1}$ 就像是一个校正透镜，把朴素系数转化为我们所寻求的系数。这意味着 ${\mathbf{X}}^{\prime }\mathbf{X}$ 是由数据的尺度和变量的相关性所引起的扭曲。

Thus I am entitled to describe linear regression as follows: I have data ($\mathbf{y}$, $\mathbf{X}$) to which I want to fit $\mathbf{y}$ = $\mathbf{Xb}$. The naive calculation is $\mathbf{b}$ = ${\mathbf{X}}^{\prime }\mathbf{y}$, which ignores the scale and correlations of the variables. The distortion caused by the scale and correlations of the variables is ${\mathbf{X}}^{\prime }\mathbf{X}$. To correct for the distortion, I map the naive coefficients through $({\mathbf{X}}^{\prime }\mathbf{X}{)}^{-1}$.
因此，我可以这样描述线性回归：我有数据（$\mathbf{y}$，$\mathbf{X}$），想拟合 $\mathbf{y}$ = $\mathbf{Xb}$。朴素计算是 $\mathbf{b}$ = ${\mathbf{X}}^{\prime }\mathbf{y}$，它忽略了变量的尺度和相关性。由变量的尺度和相关性引起的扭曲是 ${\mathbf{X}}^{\prime }\mathbf{X}$。为了校正这种扭曲，我通过 $({\mathbf{X}}^{\prime }\mathbf{X}{)}^{-1}$ 对朴素系数进行映射。

Intuition, like beauty, is in the eye of the beholder. When I learned that the variance matrix of the estimated coefficients was equal to $s^2({\mathbf{X}}^{\prime }\mathbf{X}{)}^{-1}$, I immediately thought: $s^2$ — there’s the statistics. That single statistical value is then parceled out through the corrective lens that accounts for scale and correlation. If I had data that didn’t need correcting, then the standard errors of all the coefficients would be the same and would be identical to the variance of the residuals.
直觉就像美一样，因人而异。当我得知估计系数的方差矩阵等于 $s^2({\mathbf{X}}^{\prime }\mathbf{X}{)}^{-1}$ 时，我立刻想到：$s^2$——这才是统计学的核心。这个单一的统计值然后通过考虑尺度和相关性的校正透镜进行分配。如果我有不需要校正的数据，那么所有系数的标准误差都会相同，并且与残差的方差一致。

If you go through the derivation of $s^2({\mathbf{X}}^{\prime }\mathbf{X}{)}^{-1}$, there’s a temptation to think that $s^2$ is merely something factored out from the variance matrix, probably to emphasize the connection between the variance of the residuals and standard errors. One easily loses sight of the fact that $s^2$ is the heart of the matter, just as ${\mathbf{X}}^{\prime }\mathbf{y}$ is the heart of $({\mathbf{X}}^{\prime }\mathbf{X}{)}^{-1}{\mathbf{X}}^{\prime }\mathbf{y}$. Obviously, one needs to view both $s^2$ and ${\mathbf{X}}^{\prime }\mathbf{y}$ though the same corrective lens.
如果你仔细看 $s^2({\mathbf{X}}^{\prime }\mathbf{X}{)}^{-1}$ 的推导过程，你可能会认为 $s^2$ 仅仅是从方差矩阵中提取出来的一个因子，或许是为了强调残差方差和标准误差之间的联系。但人们很容易忽略 $s^2$ 是问题的核心这一事实，就像 ${\mathbf{X}}^{\prime }\mathbf{y}$ 是 $({\mathbf{X}}^{\prime }\mathbf{X}{)}^{-1}{\mathbf{X}}^{\prime }\mathbf{y}$ 的核心一样。显然，我们需要通过同一个校正透镜来看待 $s^2$ 和 ${\mathbf{X}}^{\prime }\mathbf{y}$。

I have more to say about this way of thinking about matrices. Look for part 2 in the near future.
关于这种思考矩阵的方式，我还有更多的话要说。请关注第二部分。

---

Understanding matrices intuitively, part 2, eigenvalues and eigenvectors

直观理解矩阵（第二部分）：特征值和特征向量

$9$ March $2011$ William Gould

Visualizing Eigenvalues and Eigenvectors

可视化特征值和特征向量

Last time, I showed you a way to graph and to think about matrices. This time, I want to apply the technique to eigenvalues and eigenvectors. The point is to give you a picture that will guide your intuition, just as it was previously.
上一次，我向大家展示了一种绘制矩阵图形和思考矩阵的方法。这次，我想把这种方法应用到特征值和特征向量上。目的是给大家一个能引导直觉的图像，就像上次一样。

Before I go on, several people asked after reading part 1 for the code I used to generate the graphs. Here it is, both for part 1 and part 2: matrixcode.zip.
在我继续之前，有几个人在读完第一部分后问我用于生成这些图形的代码。这是第一部分和第二部分的代码：matrixcode.zip。

The eigenvectors and eigenvalues of matrix $\mathbf{A}$ are defined to be the nonzero $\mathbf{x}$ and $\lambda$ values that solve
矩阵 $\mathbf{A}$ 的特征向量和特征值被定义为满足以下方程的非零 $\mathbf{x}$ 和 $\lambda$：

$\mathbf{Ax}$ = $\lambda \mathbf{x}$

I wrote a lot about $\mathbf{Ax}$ in the last post. Just as previously, $\mathbf{x}$ is a point in the original, untransformed space and $\mathbf{Ax}$ is its transformed value. $\lambda$ on the right-hand side is a scalar.
在上一篇文章中，我详细讨论了 $\mathbf{Ax}$。和之前一样，$\mathbf{x}$ 是原始的、未变换空间中的一个点，$\mathbf{Ax}$ 是它的变换后的值。右边的 $\lambda$ 是一个标量。

Scalar Multiplication

标量乘法

Multiplying a point by a scalar moves the point along a line that passes through the origin and the point:
用一个标量乘以一个点，会使这个点沿着一条穿过原点和该点的直线移动：

The figure above illustrates $\mathbf{y}$=$\lambda \mathbf{x}$ when $\lambda >1$. If $\lambda$ were less than $1$, the point would move toward the origin and if $\lambda$ were also less than $0$, the point would pass right by the origin to land on the other side. For any point $\mathbf{x}$, $\mathbf{y}$=$\lambda \mathbf{x}$ will be somewhere on the line passing through the origin and $\mathbf{x}$.
上图展示了当 $\lambda >1$ 时 $\mathbf{y}$=$\lambda \mathbf{x}$ 的情况。如果 $\lambda$ 小于 $1$，这个点会向原点移动；如果 $\lambda$ 也小于 $0$，这个点会经过原点，落到另一边。对于任何点 $\mathbf{x}$，$\mathbf{y}$=$\lambda \mathbf{x}$ 都会在穿过原点和 $\mathbf{x}$ 的直线上的某个位置。

Eigenvalues and Eigenvectors

特征值和特征向量

Thus $\mathbf{Ax}$ = $\lambda \mathbf{x}$ means the transformed value $\mathbf{Ax}$ lies on a line passing through the origin and the original $\mathbf{x}$. Points that meet that restriction are eigenvectors (or more correctly, as we will see, eigenpoints, a term I just coined), and the corresponding eigenvalues are the $\lambda$‘s that record how far the points move along the line.
因此，$\mathbf{Ax}$ = $\lambda \mathbf{x}$ 意味着变换后的值 $\mathbf{Ax}$ 位于穿过原点和原始点 $\mathbf{x}$ 的直线上。满足这个限制条件的点就是特征向量（或者更准确地说，正如我们将看到的，是特征点，这是我刚刚创造的一个术语），而相应的特征值就是记录这些点沿直线移动距离的 $\lambda$。

Actually, if $\mathbf{x}$ is a solution to $\mathbf{Ax}$ = $\lambda \mathbf{x}$, then so is every other point on the line through $0$ and $\mathbf{x}$. That’s easy to see. Assume $\mathbf{x}$ is a solution to $\mathbf{Ax}$ = $\lambda \mathbf{x}$ and substitute $c\mathbf{x}$ for $\mathbf{x}$: $\mathbf{A}(c\mathbf{x})$ = $\lambda (c\mathbf{x})$. Thus $\mathbf{x}$ is not the eigenvector but is merely a point along the eigenvector.
实际上，如果 $\mathbf{x}$ 是 $\mathbf{Ax}$ = $\lambda \mathbf{x}$ 的解，那么穿过 $0$ 和 $\mathbf{x}$ 的直线上的其他所有点也是该方程的解。这很容易理解。假设 $\mathbf{x}$ 是 $\mathbf{Ax}$ = $\lambda \mathbf{x}$ 的解，用 $c\mathbf{x}$ 代替 $\mathbf{x}$：$\mathbf{A}(c\mathbf{x})$ = $\lambda (c\mathbf{x})$。因此，$\mathbf{x}$ 并不是特征向量，而仅仅是特征向量上的一个点。

And with that prelude, we are now in a position to interpret $\mathbf{Ax}$ = $\lambda \mathbf{x}$ fully. $\mathbf{Ax}$ = $\lambda \mathbf{x}$ finds the lines such that every point on the line, say, $\mathbf{x}$, transformed by $\mathbf{Ax}$ moves to being another point on the same line. These lines are thus the natural axes of the transform defined by $\mathbf{A}$.
有了这个铺垫，我们现在可以全面解释 $\mathbf{Ax}$ = $\lambda \mathbf{x}$ 了。$\mathbf{Ax}$ = $\lambda \mathbf{x}$ 找到的是这样一些直线：直线上的每个点（比如 $\mathbf{x}$）经过 $\mathbf{Ax}$ 变换后，会移动到同一条直线上的另一个点。因此，这些直线是 $\mathbf{A}$ 所定义的变换的自然轴。

The equation $\mathbf{Ax}$ = $\lambda \mathbf{x}$ and the instructions “solve for nonzero $\mathbf{x}$ and $\lambda$” are deceptive. A more honest way to present the problem would be to transform the equation to polar coordinates. We would have said to find $\theta$ and $\lambda$ such that any point on the line $(r,\theta )$ is transformed to $(\lambda r,\theta )$. Nonetheless, $\mathbf{Ax}$ = $\lambda \mathbf{x}$ is how the problem is commonly written.
方程 $\mathbf{Ax}$ = $\lambda \mathbf{x}$ 以及“求解非零 $\mathbf{x}$ 和 $\lambda$”的说明具有迷惑性。更直观的呈现这个问题的方式是将方程转换到极坐标下。我们可以说，找到 $\theta$ 和 $\lambda$，使得直线 $(r,\theta )$ 上的任何点都变换到 $(\lambda r,\theta )$。尽管如此，$\mathbf{Ax}$ = $\lambda \mathbf{x}$ 是这个问题常见的写法。

However we state the problem, here is the picture and solution for $\mathbf{A}$ = ($2$, $1$ \ $1$, $2$)
不管我们如何表述这个问题，下面是 $\mathbf{A}$ = ($2$, $1$ \ $1$, $2$) 的图形和解答：

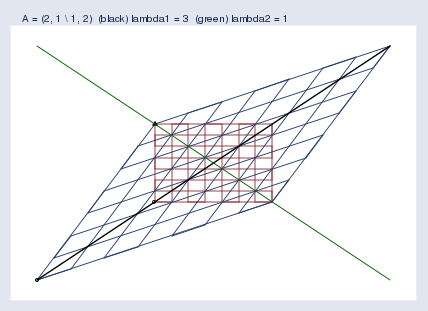
I used Mata’s $\text{eigensystem()}$ function to obtain the eigenvectors and eigenvalues. In the graph, the black and green lines are the eigenvectors.
我使用 Mata 的 $\text{eigensystem()}$ 函数来获取特征向量和特征值。在图形中，黑色和绿色的线是特征向量。

The first eigenvector is plotted in black. The “eigenvector” I got back from Mata was ($0.707$ \ $0.707$), but that’s just one point on the eigenvector line, the slope of which is $0.707/0.707=1$, so I graphed the line $\mathbf{y}$ = $\mathbf{x}$. The eigenvalue reported by Mata was $3$. Thus every point $\mathbf{x}$ along the black line moves to three times its distance from the origin when transformed by $\mathbf{Ax}$. I suppressed the origin in the figure, but you can spot it because it is where the black and green lines intersect.
第一条特征向量用黑色绘制。我从 Mata 得到的“特征向量”是 ($0.707$ \ $0.707$)，但这只是特征向量直线上的一个点，该直线的斜率是 $0.707/0.707=1$，所以我绘制了直线 $\mathbf{y}$ = $\mathbf{x}$。Mata 报告的特征值是 $3$。因此，当通过 $\mathbf{Ax}$ 变换时，黑色直线上的每个点 $\mathbf{x}$ 都会移动到距离原点三倍于原来距离的位置。我在图中隐藏了原点，但你可以找到它，因为它是黑色和绿色直线的交点。

The second eigenvector is plotted in green. The second “eigenvector” I got back from Mata was ($-0.707$ \ $0.707$), so the slope of the eigenvector line is $0.707/(-0.707)=-1$. I plotted the line $\mathbf{y}$ = $-\mathbf{x}$. The eigenvalue is $1$, so the points along the green line do not move at all when transformed by $\mathbf{Ax}$; $\mathbf{y}$=$\lambda \mathbf{x}$ and $\lambda =1$.
第二条特征向量用绿色绘制。我从 Mata 得到的第二个“特征向量”是 ($-0.707$ \ $0.707$)，所以该特征向量直线的斜率是 $0.707/(-0.707)=-1$。我绘制了直线 $\mathbf{y}$ = $-\mathbf{x}$。特征值是 $1$，所以当通过 $\mathbf{Ax}$ 变换时，绿色直线上的点根本不会移动；$\mathbf{y}$=$\lambda \mathbf{x}$ 且 $\lambda =1$。

Eigenpoints and Eigenaxes

特征点和特征轴

Here’s another example, this time for the matrix $\mathbf{A}$ = ($1.1$, $2$ \ $3$, $1$):
再来看另一个例子，这次是矩阵 $\mathbf{A}$ = ($1.1$, $2$ \ $3$, $1$)：

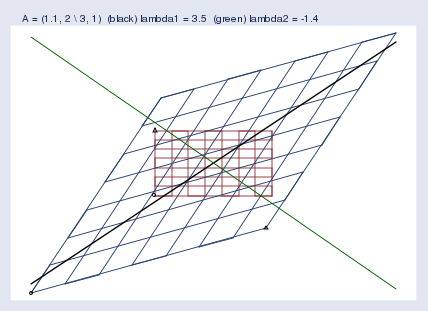
The first “eigenvector” and eigenvalue Mata reported were… Wait! I’m getting tired of quoting the word eigenvector. I’m quoting it because computer software and the mathematical literature call it the eigenvector even though it is just a point along the eigenvector. Actually, what’s being described is not even a vector. A better word would be eigenaxis. Since this posting is pedagogical, I’m going to refer to the computer-reported eigenvector as an eigenpoint along the eigenaxis. When you return to the real world, remember to use the word eigenvector.
Mata 报告的第一个“特征向量”和特征值是……等等！我厌倦了给“特征向量”这个词加引号了。我加引号是因为计算机软件和数学文献都称它为特征向量，尽管它只是特征向量上的一个点。实际上，所描述的甚至不是一个向量。一个更好的词是特征轴。由于这篇文章是教学性的，我会把计算机报告的特征向量称为特征轴上的特征点。当你回到实际应用中时，记得使用“特征向量”这个词。

The first eigenpoint and eigenvalue that Mata reported were ($0.640$ \ $0.768$) and $\lambda$ = $3.45$. Thus the slope of the eigenaxis is $0.768/0.640=1.2$, and points along that line — the green line — move to $3.45$ times their distance from the origin.
Mata 报告的第一个特征点和特征值是 ($0.640$ \ $0.768$) 和 $\lambda$ = $3.45$。因此，特征轴的斜率是 $0.768/0.640=1.2$，这条直线（绿色直线）上的点会移动到距离原点 $3.45$ 倍于原来距离的位置。

The second eigenpoint and eigenvalue Mata reported were ($-0.625$ \ $0.781$) and $\lambda$ = $-1.4$. Thus the slope is $-0.781/0.625=-1.25$, and points along that line move to $-1.4$ times their distance from the origin, which is to say they flip sides and then move out, too. We saw this flipping in my previous posting. You may remember that I put a small circle and triangle at the bottom left and bottom right of the original grid and then let the symbols be transformed by $\mathbf{A}$ along with the rest of space. We saw an example like this one, where the triangle moved from the top-left of the original space to the bottom-right of the transformed space. The space was flipped in one of its dimensions. Eigenvalues save us from having to look at pictures with circles and triangles; when a dimension of the space flips, the corresponding eigenvalue is negative.
Mata 报告的第二个特征点和特征值是 ($-0.625$ \ $0.781$) 和 $\lambda$ = $-1.4$。因此，斜率是 $-0.781/0.625=-1.25$，这条直线上的点会移动到距离原点 $-1.4$ 倍于原来距离的位置，也就是说，它们会翻转到另一边，然后也向外移动。在上一篇文章中，我们看到过这种翻转。你可能还记得，我在原始网格的左下和右下位置放了一个小圆圈和一个三角形，然后让这些符号和空间的其他部分一起被 $\mathbf{A}$ 变换。我们看到过类似这样的例子，三角形从原始空间的左上位置移动到了变换后空间的右下位置。空间在其中一个维度上发生了翻转。特征值让我们不必再看带有圆圈和三角形的图片；当空间的某个维度发生翻转时，相应的特征值是负数。

Near Singularity with Eigenaxes

近奇异矩阵与特征轴

We examined near singularity last time. Let’s look again, and this time add the eigenaxes:
上次我们研究了近奇异性。让我们再看一次，这次加上特征轴：

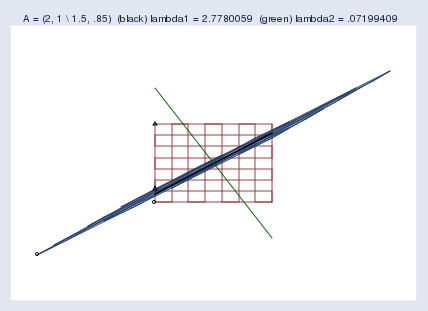
The blue blob going from bottom-left to top-right is both the compressed space and the first eigenaxis. The second eigenaxis is shown in green.
从左下到右上的蓝色团块既是压缩后的空间，也是第一条特征轴。第二条特征轴用绿色显示。

Mata reported the first eigenpoint as ($0.789$ \ $0.614$) and the second as ($-0.460$ \ $0.888$). Corresponding eigenvalues were reported as $2.78$ and $0.07$. I should mention that zero eigenvalues indicate singular matrices and small eigenvalues indicate nearly singular matrices. Actually, eigenvalues also reflect the scale of the matrix. A matrix that compresses the space will have all of its eigenvalues be small, and that is not an indication of near singularity. To detect near singularity, one should look at the ratio of the largest to the smallest eigenvalue, which in this case is $0.07/2.78=0.03$.
Mata 报告的第一个特征点是 ($0.789$ \ $0.614$)，第二个是 ($-0.460$ \ $0.888$)。相应的特征值分别是 $2.78$ 和 $0.07$。我应该提到，零特征值表明矩阵是奇异矩阵，小特征值表明矩阵是近奇异矩阵。实际上，特征值也反映了矩阵的尺度。一个压缩空间的矩阵，其所有特征值都会很小，但这并不表明它是近奇异矩阵。要检测近奇异性，应该看最大特征值与最小特征值的比值，在这个例子中是 $0.07/2.78=0.03$。

Despite appearances, computers do not find $0.03$ to be small and thus do not think of this matrix as being nearly singular. This matrix gives computers no problem; Mata can calculate the inverse of this without losing even one binary digit. I mention this and show you the picture so that you will have a better appreciation of just how squished the space can become before computers start complaining.
尽管看起来如此，计算机并不认为 $0.03$ 很小，因此也不认为这个矩阵是近奇异的。这个矩阵不会给计算机带来问题；Mata 可以计算它的逆矩阵，甚至不会丢失一个二进制位。我提到这一点并给你看这张图片，是为了让你更好地理解，在计算机开始出现问题之前，空间可以被压缩到何种程度。

When do well-programmed computers complain? Say you have a matrix $\mathbf{A}$ and make the above graph, but you make it really big — $3$ miles by $3$ miles. Lay your graph out on the ground and hike out to the middle of it. Now get down on your knees and get out your ruler. Measure the spread of the compressed space at its widest part. Is it an inch? That’s not a problem. One inch is roughly $5\times 10^{-6}$ of the original space (that is, $1$ inch by $3$ miles wide). If that were a problem, users would complain. It is not problematic until we get around $10^{-8}$ of the original area. Figure about $0.002$ inches.
程序编写良好的计算机在什么时候会出现问题呢？假设你有一个矩阵 $\mathbf{A}$，并绘制了上面这样的图形，但你把图形做得非常大——$3$ 英里乘 $3$ 英里。把图形铺在地上，走到中间。现在蹲下，拿出尺子，测量压缩空间最宽处的跨度。有一英寸吗？这没问题。一英寸大约是原始空间的 $5\times 10^{-6}$（即 $1$ 英寸比 $3$ 英里宽）。如果这都是问题的话，用户早就会抱怨了。直到压缩到原始面积的 $10^{-8}$ 左右时，才会出现问题。大概是 $0.002$ 英寸。

Further Insights into Eigenvalues and Eigenvectors

关于特征值和特征向量的更多见解

There’s more I could say about eigenvalues and eigenvectors. I could mention that rotation matrices have no eigenvectors and eigenvalues, or at least no real ones. A rotation matrix rotates the space, and thus there are no transformed points that are along their original line through the origin. I could mention that one can rebuild the original matrix from its eigenvectors and eigenvalues, and from that, one can generalize powers to matrix powers. It turns out that ${\mathbf{A}}^{-1}$ has the same eigenvectors as $\mathbf{A}$; its eigenvalues are ${\lambda }^{-1}$ of the original’s. Matrix $\mathbf{AA}$ also has the same eigenvectors as $\mathbf{A}$; its eigenvalues are ${\lambda }^2$. Ergo, ${\mathbf{A}}^p$ can be formed by transforming the eigenvalues, and it turns out that, indeed, ${\mathbf{A}}^{1/2}$ really does, when multiplied by itself, produce $\mathbf{A}$.
关于特征值和特征向量，我还有更多可以说的。我可以提到旋转矩阵没有特征向量和特征值，或者至少没有实特征向量和实特征值。旋转矩阵会旋转空间，因此不存在变换后仍在穿过原点的原始直线上的点。我可以提到，人们可以根据矩阵的特征向量和特征值重建原始矩阵，由此可以将幂运算推广到矩阵幂运算。事实证明，${\mathbf{A}}^{-1}$ 与 $\mathbf{A}$ 有相同的特征向量，其特征值是原始特征值的 ${\lambda }^{-1}$。矩阵 $\mathbf{AA}$ 也与 $\mathbf{A}$ 有相同的特征向量，其特征值是 ${\lambda }^2$。因此，${\mathbf{A}}^p$ 可以通过对特征值进行变换来得到，而且事实证明，${\mathbf{A}}^{1/2}$ 与自身相乘确实会得到 $\mathbf{A}$。

---

via:

• Understanding matrices intuitively, part 1 - The Stata Blog
  https://blog.stata.com/2011/03/03/understanding-matrices-intuitively-part-1/
• Understanding matrices intuitively, part 2, eigenvalues and eigenvectors - The Stata Blog
  https://blog.stata.com/2011/03/09/understanding-matrices-intuitively-part-2/