当前位置： 首页 > news >正文

数据结构--------堆

news 2025/8/15 5:34:40

目录

二叉树

树的概念与结构

非树形结构：

注意：

树的相关术语

树的表示

孩子兄弟表示法

树形结构实际运用场景（拓展）

1. 文件系统管理

2. 数据库与索引

3. 编程语言与数据结构

信息组织与展示

1. 思维导图

2. 目录与导航

3. 组织架构图

网络与通信

1. 路由算法

2. XML/JSON 数据格式

二叉树：

概念与结构

特点：

特殊的二叉树

满二叉树

完全二叉树​编辑

二叉树的性质

二叉树的存储结构

顺序存储结构

链式存储结构

实现顺序结构二叉树

堆的概念与结构

堆的特性：

⼆叉树性质（左右孩子位置）

实现堆的顺序结构

堆的结构体

核心函数功能

初始化

打印

交换数据

向上调整法

细节：

入堆

注意：

时间复杂度

判空

向下调整法

带入实例：

时间复杂度

删除堆顶元素：

获取堆顶元素

堆的销毁

测试代码（堆排序---向下调整法建堆）

向上调整法建堆

步骤：

代码实现（完整）：

向上向下建堆方法时间复杂度

向下调整法

向上调整法

二叉树

树的概念与结构

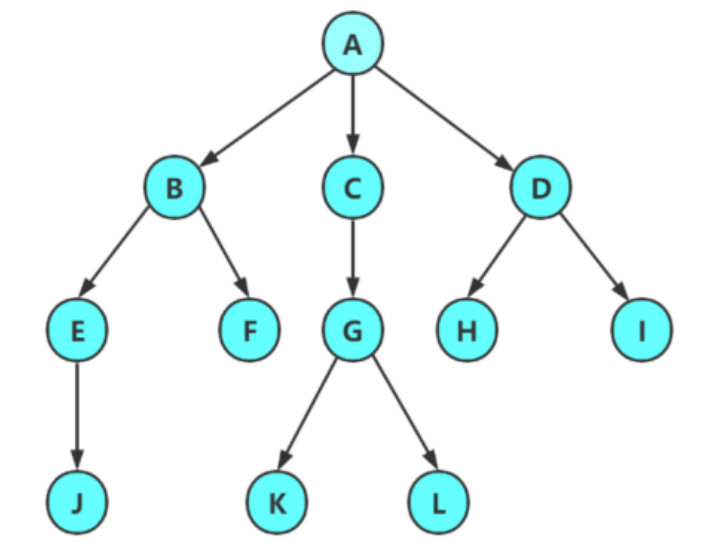
树是⼀种⾮线性的数据结构，它是由 n（n>=0） 个有限结点组成⼀个具有层次关系的集合。把它叫做树是因为它看起来像⼀棵倒挂的树，也就是说它是根朝上，而叶朝下的。

根节点：有一个特殊的结点，称为根节点，即A，根节点没有前驱节点

除根节点外，其余节点被分为互不相交的集合，且每个集合有结构与树类似的子树。子树根节点有且只有一个前驱，有0个或者多个后继。

非树形结构：

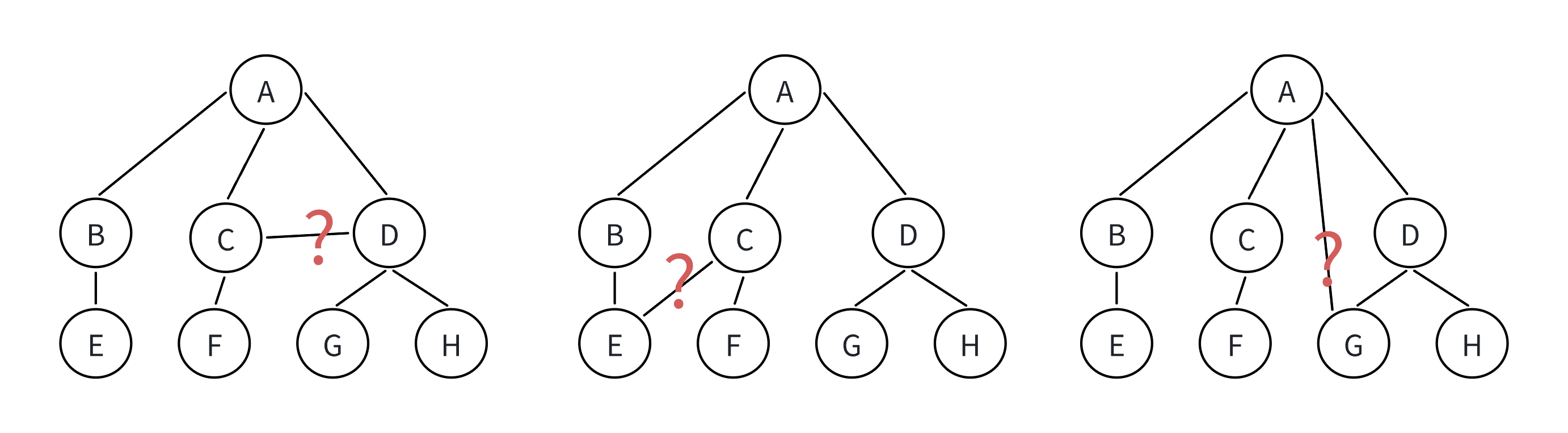
注意：

1.  子树是不相交的
2.   除了根结点外，每个结点有且仅有⼀个父结点
3.   ⼀棵N个结点的树有N-1

树的相关术语

父结点/双亲结点：若⼀个结点含有子结点，则这个结点称为其子结点的父结点； 如上图：A是B的父结点
子结点/孩子结点：⼀个结点含有的子树的根结点称为该结点的子结点； 如上图：B是A的孩子结点
结点的度：⼀个结点有几个孩子，他的度就是多少；比如A的度为6，F的度为2，K的度为0
树的度：⼀棵树中，最大的结点的度称为树的度； 如上图：树的度为 6
叶子结点/终端结点：度为 0 的结点称为叶结点； 如上图： B、C、H、I... 等结点为叶结点
分支结点/非终端结点：度不为 0 的结点； 如上图： D、E、F、G... 等结点为分支结点
兄弟结点：具有相同⽗结点的结点互称为兄弟结点(亲兄弟)； 如上图： B、C 是兄弟结点
结点的层次：从根开始定义起，根为第 1 层，根的子结点为第 2 层，以此类推；
树的⾼度或深度：树中结点的最大层次； 如上图：树的高度为 4
结点的祖先：从根到该结点所经分⽀上的所有结点；如上图： A 是所有结点的祖先
路径：⼀条从树中任意节点出发，沿父节点-子节点连接，达到任意节点的序列；比如A到Q的路径为： A-E-J-Q；H到Q的路径H-D-A-E-J-Q
子孙：以某结点为根的子树中任⼀结点都称为该结点的子孙。如上图：所有结点都是A的子孙
森林：由 m（m>0） 棵互不相交的树的集合称为森林； 

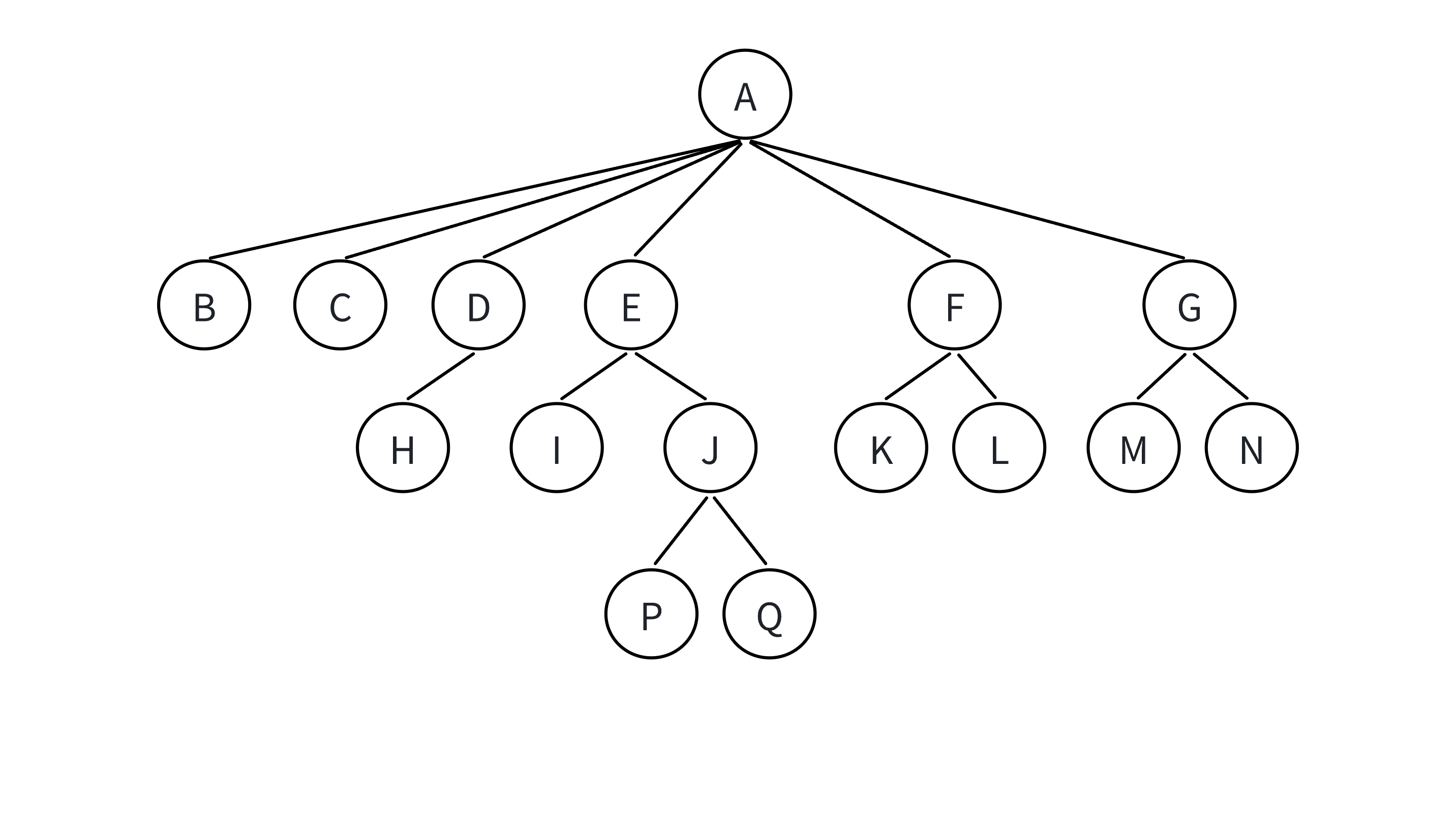
树的表示

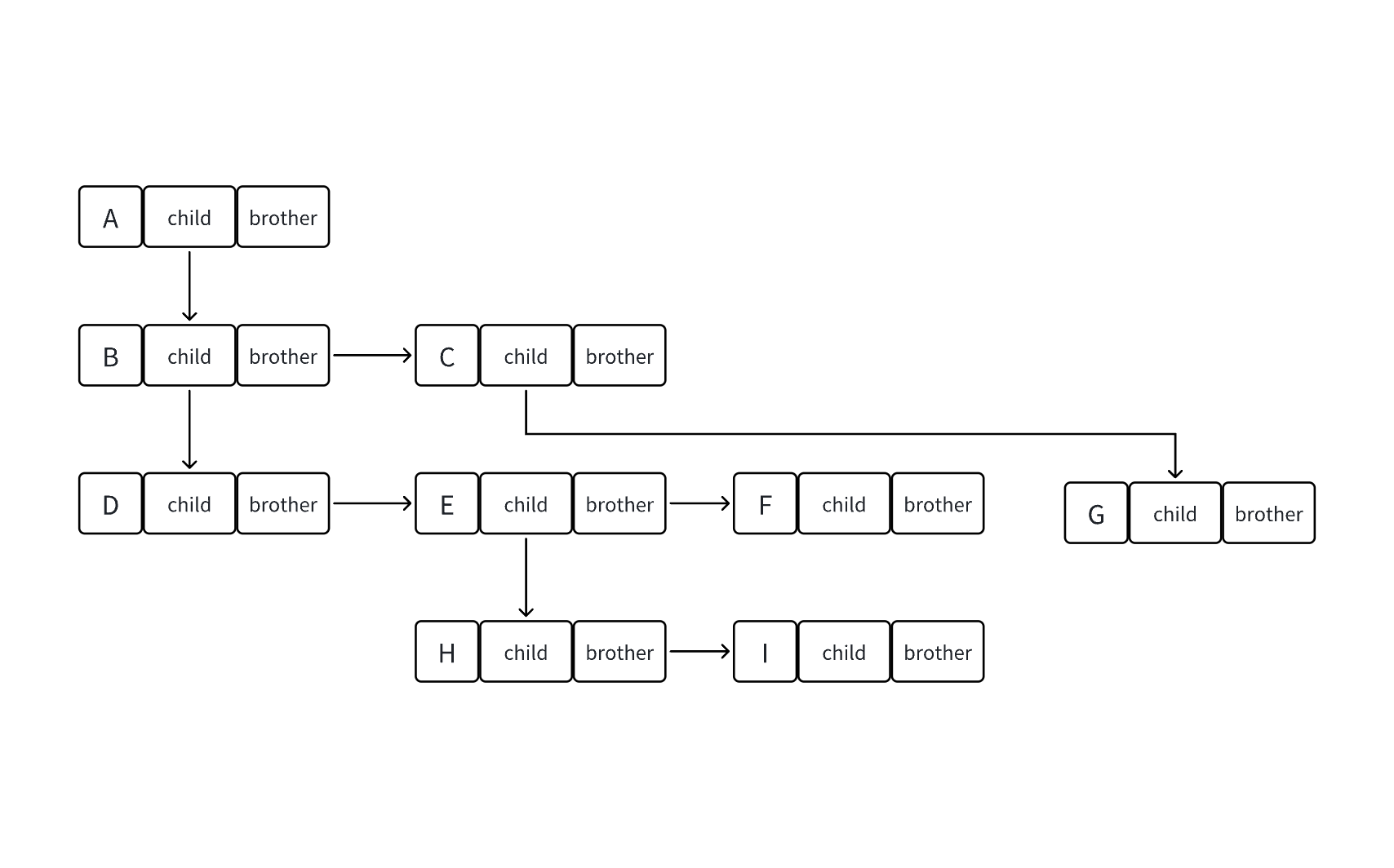
孩子兄弟表示法

struct TreeNode
{struct TreeNode* child;//左边开始第一个孩子节点struct TreeNode* brother;//指向右边的下一个兄弟结点int data;//存储的数据
};

树形结构实际运用场景（拓展）

1. 文件系统管理
  • 操作系统（如 Windows、Linux）的文件目录结构是最经典的树形结构：
    • 根目录（如C:\、/）为 “根节点”；
    • 子文件夹为 “中间节点”；
    • 具体文件为 “叶子节点”。
  • 优势：通过层级路径（如/user/doc/report.pdf）快速定位文件，支持递归遍历和批量操作。
2. 数据库与索引
  • B 树 / B + 树：数据库（如 MySQL）的索引结构，通过多层节点快速定位数据，平衡了查询效率和磁盘存储性能。
  • 树形查询：用于表示数据库中的 “父子关系”（如部门与子部门、评论与回复），通过递归查询获取完整层级数据。
3. 编程语言与数据结构
  • 语法树（AST）：编译器将代码解析为树形结构，用于语法分析和执行（如 Python、Java 的代码执行过程）。
  • DOM 树：HTML/XML 文档的解析结构，每个标签为节点，支持通过 JavaScript 遍历或修改页面元素（如document.getElementById）。
  • 红黑树 / AVL 树：高效的平衡查找树，用于实现TreeMap（Java）或map（C++）等数据结构，支持 O (log n) 的插入、删除和查询。

信息组织与展示

1. 思维导图
  • 以核心主题为根节点，分支延伸子主题，用于 brainstorming、知识梳理（如 XMind、MindNode 工具）。
2. 目录与导航
  • 书籍的章节结构、网站的导航菜单（如电商网站的 “商品分类→子分类→商品”），通过层级关系帮助用户快速定位信息。
3. 组织架构图
  • 企业或机构的层级关系（如 “CEO→部门经理→员工”），清晰展示上下级隶属关系。

网络与通信

1. 路由算法
  • 网络中的路由表常以树形结构表示，通过最短路径算法（如 Dijkstra）在节点间传递数据，减少冗余路径。
2. XML/JSON 数据格式

  • 半结构化数据的嵌套结构本质是树形（如 JSON 的{ "a": { "b": "c" } }），便于存储层级化信息（如配置文件、API 返回数据）。

二叉树：

概念与结构

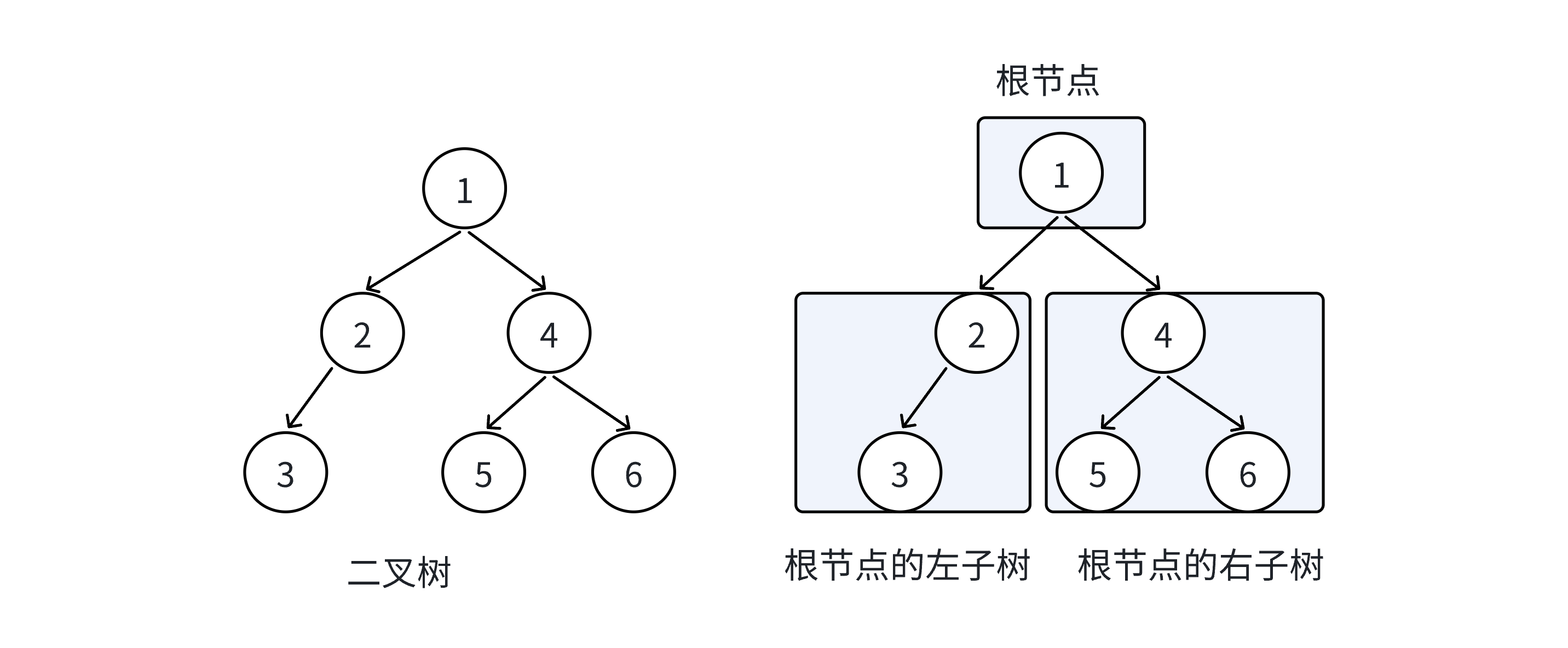
在树形结构中，我们最常⽤的就是⼆叉树，⼀棵⼆叉树是结点的⼀个有限集合，该集合由⼀个根结点 加上两棵别称为左⼦树和右⼦树的⼆叉树组成或者为空。

特点：

1.二叉树不存在度大于2的结点

2.二叉树子树有左右之分，次序不能颠倒，是有序树

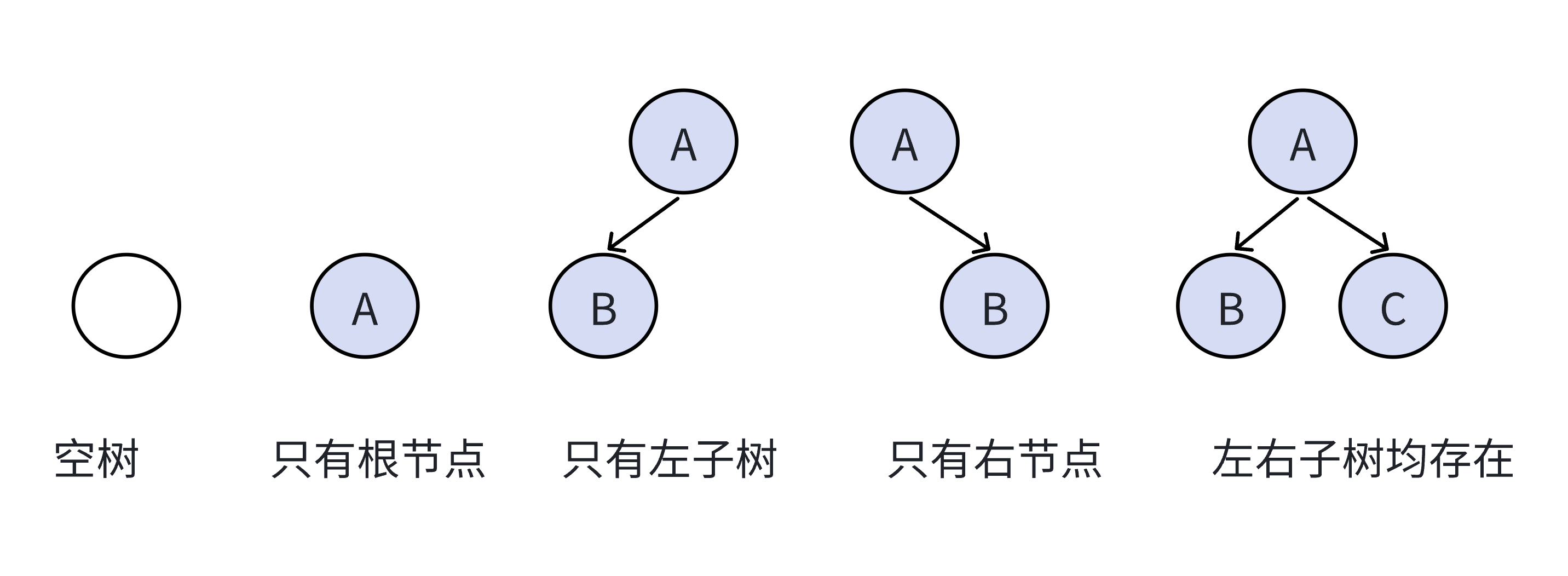
特殊的二叉树

满二叉树

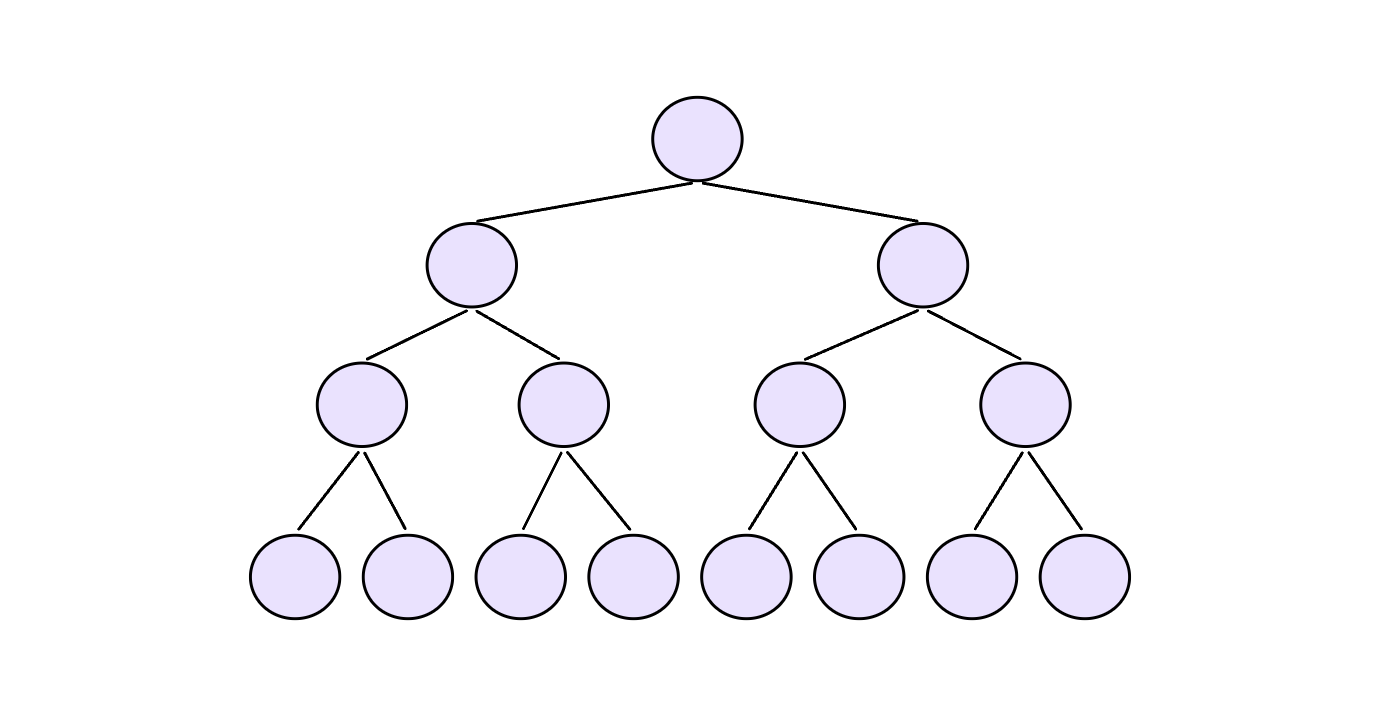
⼀个⼆叉树，如果每⼀个层的结点数都达到最⼤值，则这个⼆叉树就是满⼆叉树。

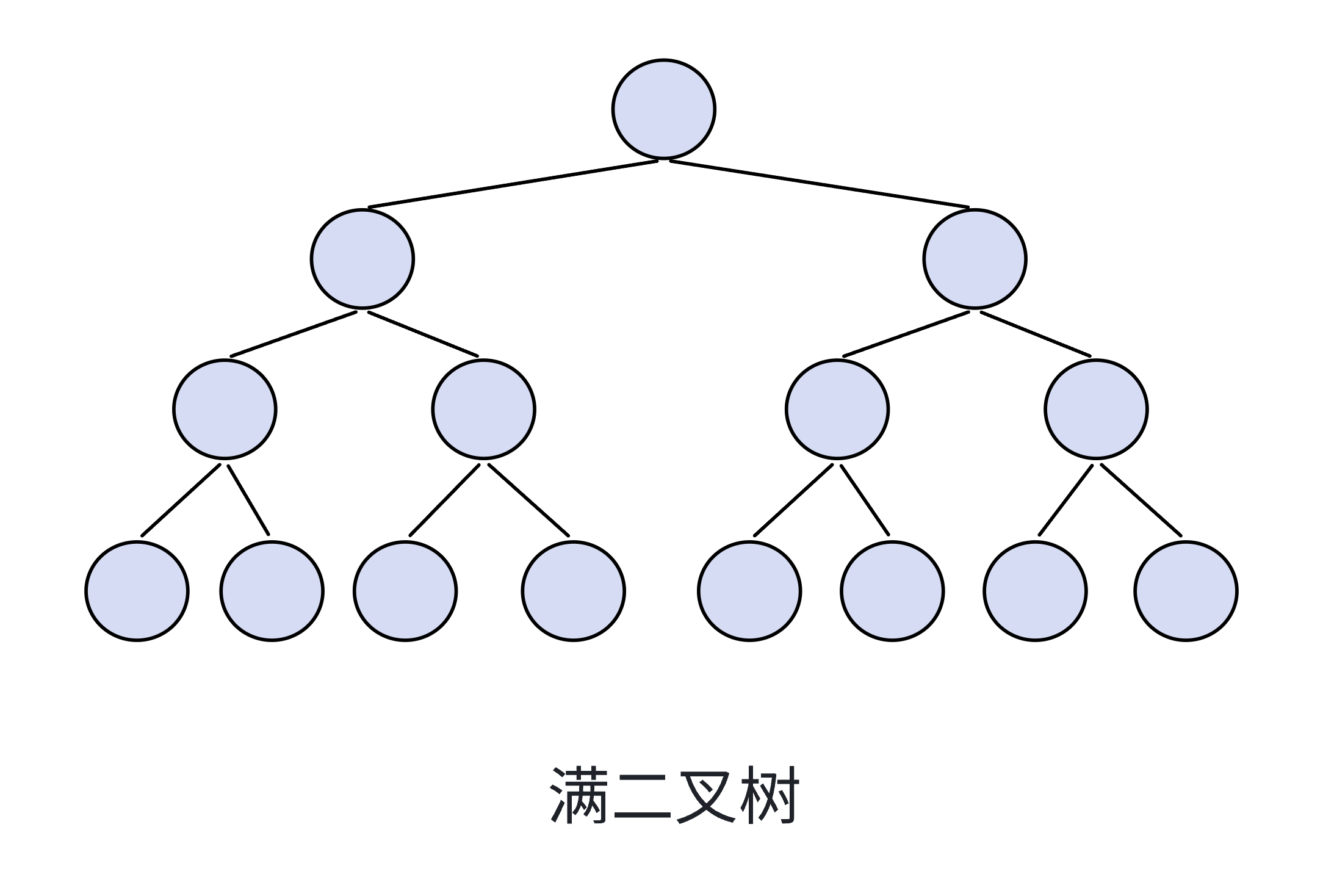
其层数若为n ,则节点数有2^n-1个

完全二叉树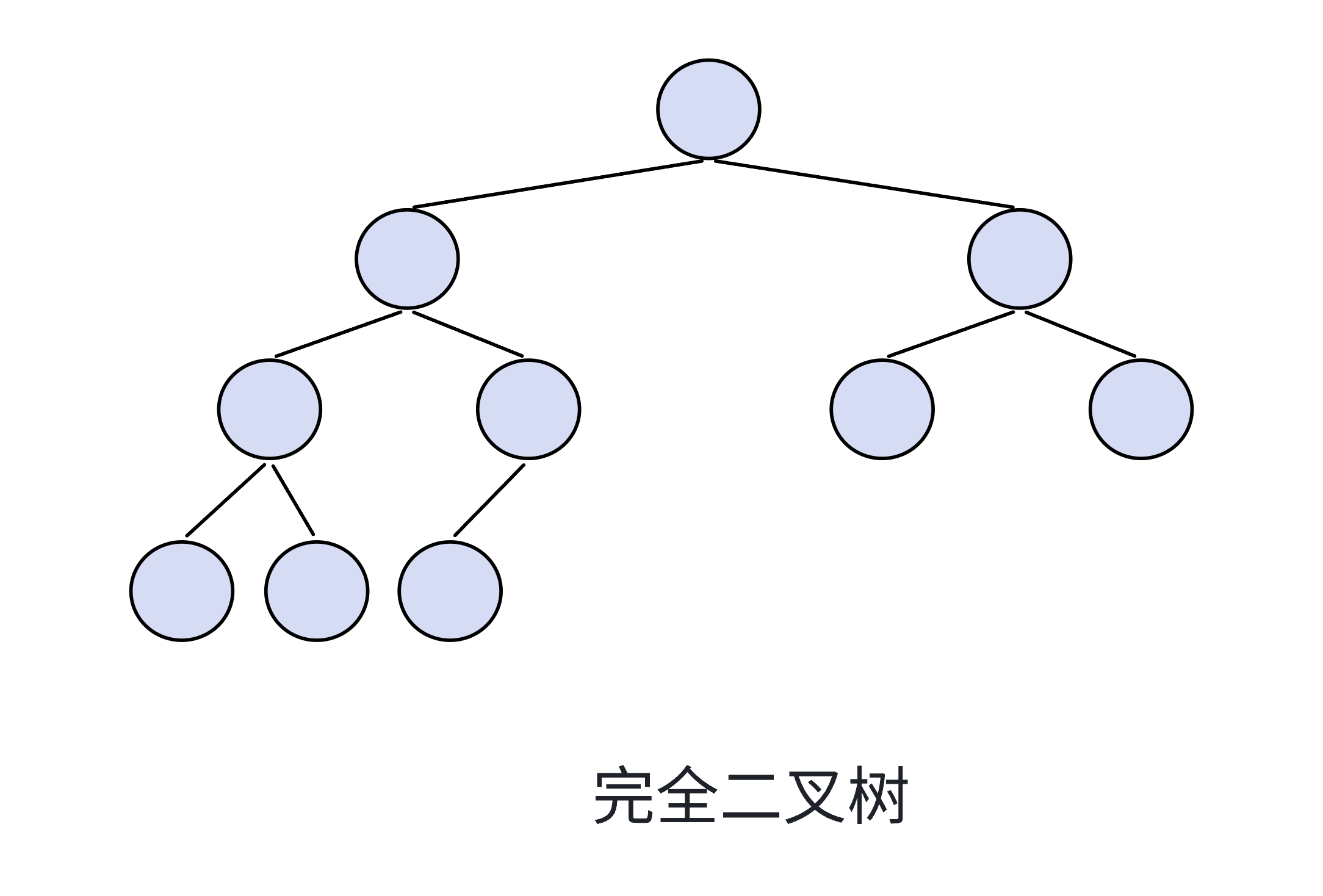

完全⼆叉树是效率很高的数据结构，完全⼆叉树是由满⼆叉树⽽引出来的。对于深度为 K 的，有 n 个结点的⼆叉树，当且仅当其每⼀个结点都与深度为K的满⼆叉树中编号从 1 ⾄ n 的结点⼀⼀对应时称之为完全⼆叉树。要注意的是满⼆叉树是⼀种特殊的完全⼆叉树。
二叉树的性质
根据满⼆叉树的特点可知：
1）若规定根结点的层数为 1 ，则⼀棵⾮空⼆叉树的第i层上最多有 2 ^（i−1） 个结点
2）若规定根结点的层数为 1 ，则深度为 h 的⼆叉树的最⼤结点数是 2^ h − 1
3）若规定根结点的层数为 1 ，具有 n 个结点的满⼆叉树的深度 h = log2 (n + 1) ( log
以2为底， n+1 为对数)

二叉树的存储结构

顺序存储结构

顺序存储结构使用数组（或列表）来存储二叉树的节点，通过节点在数组中的位置关系来体现二叉

树的逻辑结构。

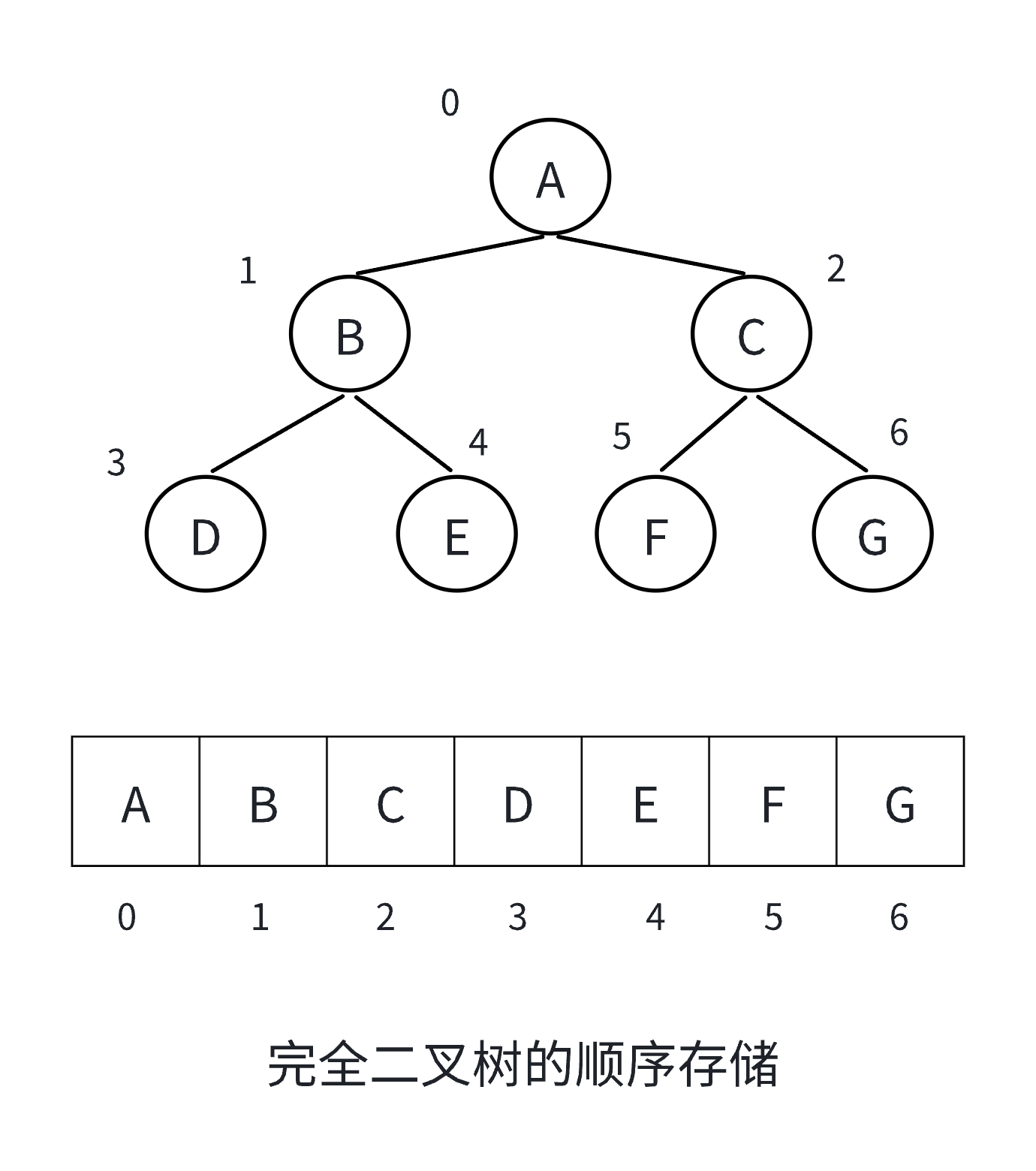
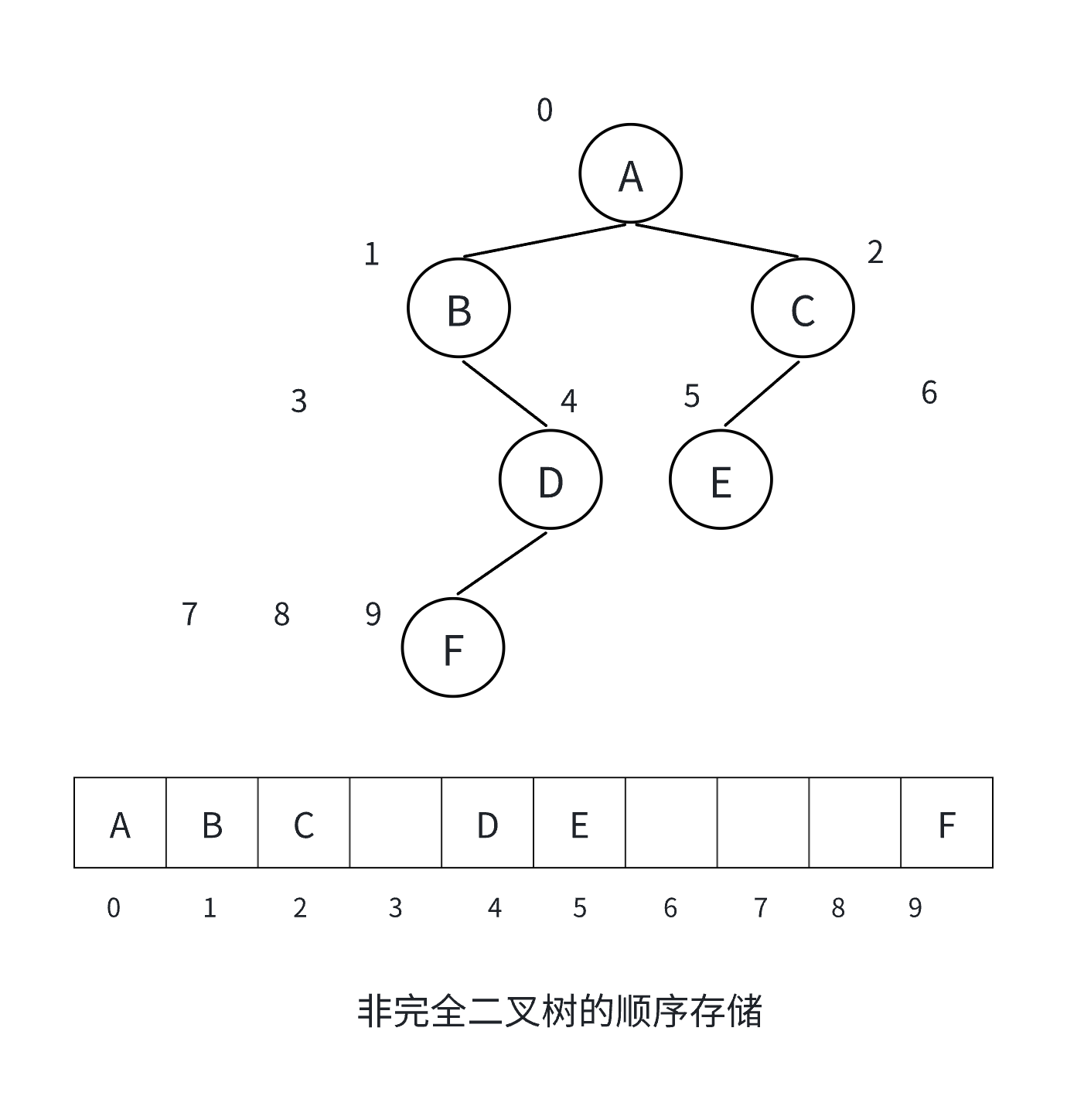
⼀般使⽤数组只适合表示完全⼆叉树，因为不是完全⼆叉树会有 空间的浪费，完全⼆叉树更适合使⽤顺序结构存储。

若根节点存储在数组下标为 i 的位置：

  • 左孩子节点存储在 2i + 1 的位置
  • 右孩子节点存储在 2i + 2 的位置

优缺点：

  • 优点：访问节点速度快，通过索引可直接访问，节省存储空间（无需存储指针）
  • 缺点：只适合存储完全二叉树，对于非完全二叉树会浪费大量空间；插入和删除操作不方便

链式存储结构

用链表来表示⼀棵⼆叉树，每个节点包含数据域和指向左右孩子的指针域。

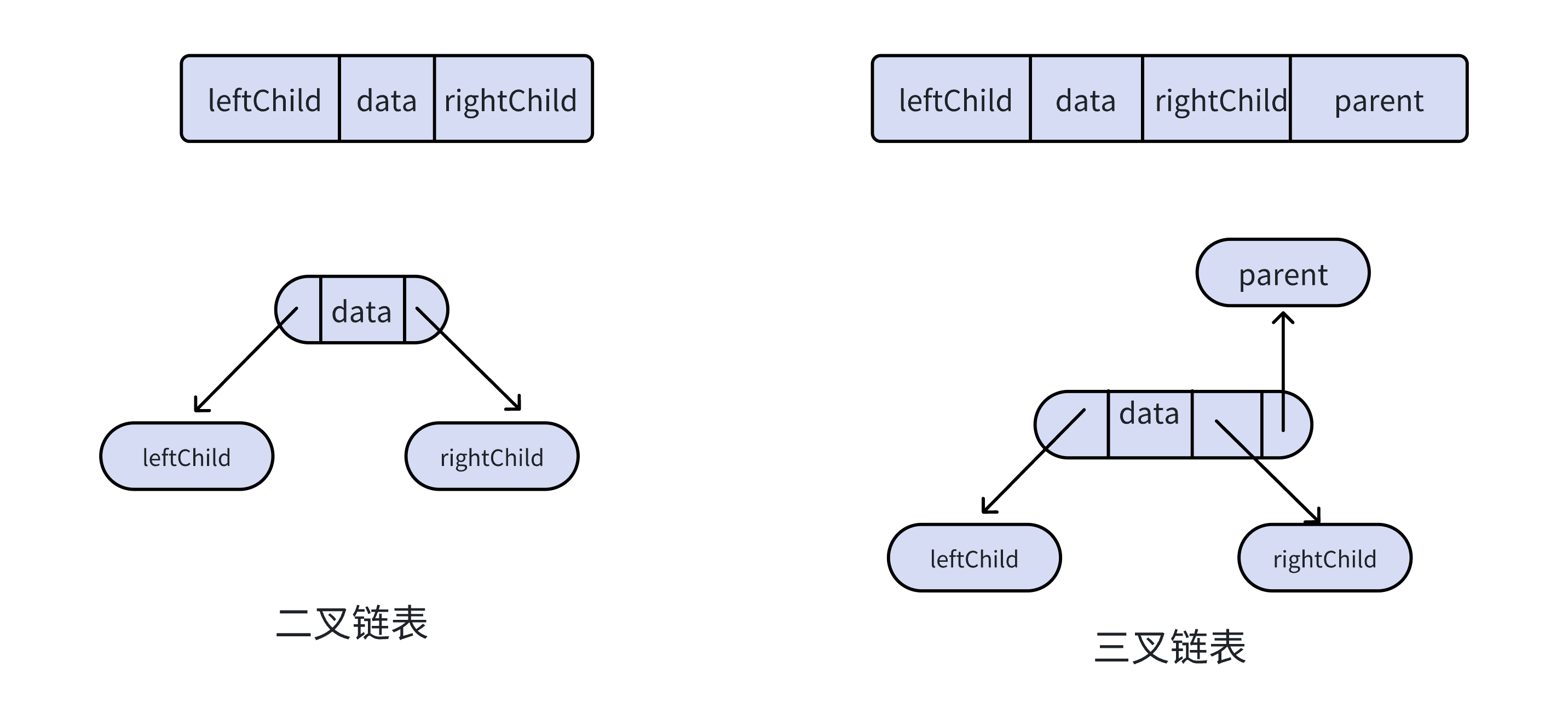
优缺点：

  • 优点：空间利用率高，适合存储各种形态的二叉树；插入和删除操作灵活方便
  • 缺点：访问节点需要通过指针遍历，访问效率相对较低；需要额外存储空间存储指针

实现顺序结构二叉树

⼀般堆使用顺序结构的数组来存储数据，堆是⼀种特殊的⼆叉树，具有⼆叉树的特性的同时，还具备其他的特性。

堆的概念与结构

堆的特性：

  • 结构特性：堆是一棵完全二叉树，即除最后一层外，其他层的节点都被填满，且最后一层的节点从左到右依次排列
  • 堆序特性：
    • 大根堆（Max Heap）：每个父节点的值大于或等于其左右孩子节点的值
    • 小根堆（Min Heap）：每个父节点的值小于或等于其左右孩子节点的值

堆具有以下性质：
•   堆中某个结点的值总是不大于或不小于其父结点的值；
•   堆总是⼀棵完全⼆叉树。

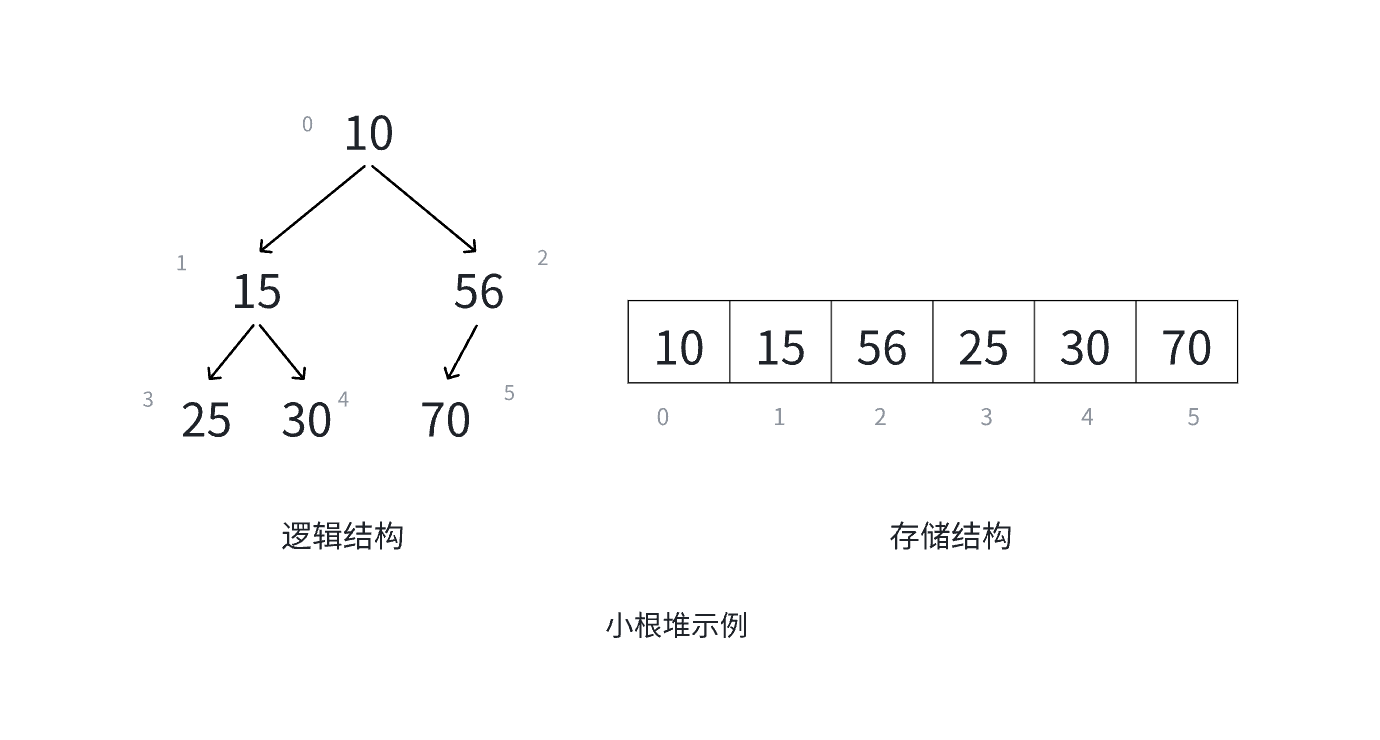
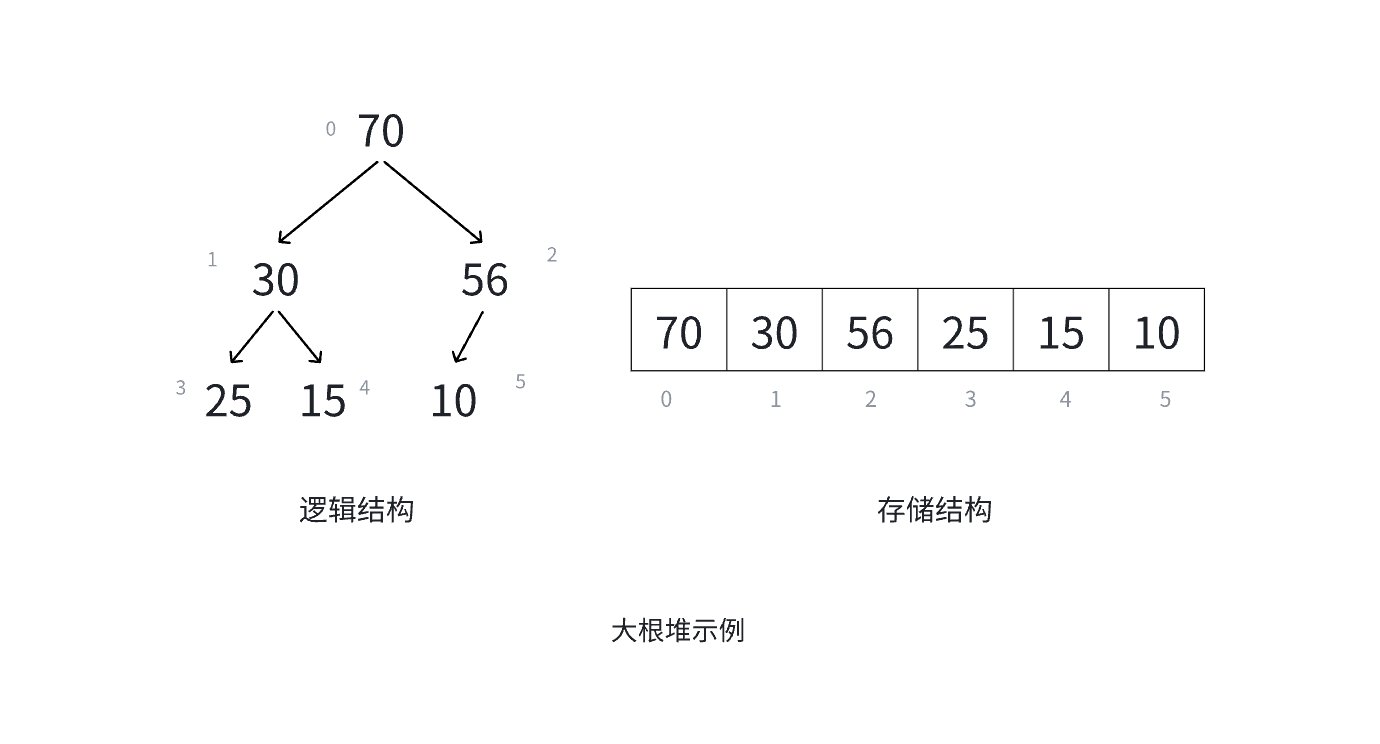
⼆叉树性质（左右孩子位置）

对于具有 n 个结点的完全⼆叉树，如果按照从上至下从左至右的数组顺序对所有结点从
0 开始编号，则对于序号为 i 的结点有：
1. 若 i>0 ， i 位置结点的双亲序号： (i-1)/2 ； i=0 ， i 为根结点编号，无双亲结点
2. 若 2i+1<n ，左孩子序号： 2i+1 ， 2i+1>=n 否则无左孩子
3. 若 2i+2<n ，右孩子序号： 2i+2 ， 2i+2>=n 否则无右孩子

实现堆的顺序结构

堆的结构体

typedef int HPDataType;  // 堆中存储的数据类型
typedef struct Heap {HPDataType* arr;    // 存储堆元素的数组int size;           // 当前堆中元素的数量int capacity;       // 堆的容量
} HP;

核心函数功能

  • HPInit：初始化堆，将数组指针置空，大小和容量设为 0
  • HPDestroy：销毁堆，释放动态分配的内存
  • HPPrint：打印堆中的所有元素
  • Swap：交换两个整数的值
  • AdjustUp：向上调整算法，用于插入元素后维持堆的性质
  • HPPush：向堆中插入元素
  • HPEmpty：判断堆是否为空
  • AdjustDown：向下调整算法，用于删除元素后维持堆的性质
  • HPPop：删除堆顶元素
  • HPTop：获取堆顶元素的值
void HPInit(HP* php);
void HPDestroy(HP* php);
void HPPrint(HP* php);void Swap(int* x, int* y);
void AdjustUp(HPDataType* arr, int child);
void AdjustDown(HPDataType* arr, int parent, int n);void HPPush(HP* php, HPDataType x);
void HPPop(HP* php);
//取堆顶数据
HPDataType HPTop(HP* php);// 判空
bool HPEmpty(HP* php);
初始化
void HPInit(HP* php)
{php->arr = NULL;php->size = php->capacity = 0;
}
打印
void HPPrint(HP* php)
{for (int i = 0; i < php->size; i++){printf("%d ", php->arr[i]);}printf("\n");
}
交换数据
void Swap(int* x, int* y)
{int tmp = *x;*x = *y;*y = tmp;
}

如果不用指针，直接传递变量的值，函数内部的交换操作不会影响到函数外部的变量

向上调整法
void AdjustUp(HPDataType* arr, int child)
{int parent = (child - 1) / 2;while (child > 0){//大堆：>//小堆：<if (arr[child] > arr[parent]){//调整Swap(&arr[child], &arr[parent]);child = parent;parent = (child - 1) / 2;}else {break;}}
}

当新元素被插入到堆的末尾时，可能会破坏堆的性质（父节点值大于子节点值）。AdjustUp 函数通过将新插入的元素（从最后一个位置）向上移动，与父节点比较并交换，直到重新满足堆的性质。

细节：

  1. 父节点索引计算公式 (child - 1) / 2 是由完全二叉树的性质决定的

  2. 循环终止条件 child > 0 确保不会越界访问（根节点没有父节点）

  3. 若要实现小根堆，只需将比较运算符 > 改为 <

入堆
//入堆
void HPPush(HP* php, HPDataType x)
{assert(php);//判断空间是否足够if (php->size == php->capacity){int newCapacity = php->capacity == 0 ? 4 : 2 * php->capacity;HPDataType* tmp = (HPDataType*)realloc(php->arr, newCapacity * sizeof(HPDataType));if (tmp == NULL){perror("realloc fail!");exit(1);}php->arr = tmp;php->capacity = newCapacity;}php->arr[php->size] = x;//向上调整AdjustUp(php->arr, php->size);++php->size;
}
  • 新元素先放在数组末尾（对应完全二叉树的最后一个位置）
  • 调用AdjustUp函数向上调整，确保插入后仍满足堆的性质
  • 最后更新堆的元素数量
注意：

realloc 的核心作用是重新分配已有的动态内存块，可以：

  • 当原内存块后面有足够空间时，直接在原地扩展，无需复制数据
  • 当空间不足时，自动分配新内存块并将原数据复制过去
    而 malloc 只能分配全新的内存块，如果用 malloc 实现扩容，需要手动完成
  • 当堆的内存块后面有连续的空闲空间时，realloc 可以直接扩展内存，避免数据复制，效率远高于 malloc + memcpy + free 的组合。
时间复杂度
  • 扩容操作的时间复杂度：O (n)（最坏情况，需要复制所有元素），但由于采用 2 倍扩容策略，平均下来是 O (1)
  • 向上调整操作的时间复杂度：O (log n)（最多需要调整到根节点，路径长度为堆的高度）
  • 因此，HPPush操作的平均时间复杂度为 O (log n)。
判空
// 判空
bool HPEmpty(HP* php)
{assert(php);return php->size == 0;
}
向下调整法
//向下调整算法
void AdjustDown(HPDataType* arr, int parent, int n)
{int child = parent * 2 + 1;//左孩子while (child < n){//大堆：<//小堆：>if (child + 1 < n && arr[child] < arr[child + 1]){child++;}//大堆: >//小堆：<if (arr[child] > arr[parent]){//调整Swap(&arr[child], &arr[parent]);parent = child;child = parent * 2 + 1;}else {break;}}
}
  • HPDataType* arr：存储堆元素的数组
  • int parent：需要向下调整的起始父节点索引（通常是堆顶元素索引 0）
  • int n：堆中有效元素的个数（调整范围不超过此值）

  • 关键细节：

    • 先判断右孩子是否存在且更大（child + 1 < n确保不越界），目的是找到两个孩子中的最大值
    • 若子节点大于父节点，交换后继续向下调整；否则说明已满足堆性质，停止调整
    • 若要实现小根堆，只需将两处比较运算符<和>分别改为>和<
带入实例：

假设大根堆当前状态为 [60, 50, 40, 30]，删除堆顶元素后，最后一个元素30移到堆顶，数组变为 [30, 50, 40, ...]（size减 1 后n=3）：

 
时间复杂度

AdjustDown的时间复杂度为O(log n)，因为最多需要调整到堆的最底层，路径长度为堆的高度（完全二叉树的高度为log2(n+1)）。

  1. parent=0，child=1（左孩子 50）
  2. 右孩子child+1=2（值 40）存在，50>40，所以child保持 1
  3. 子节点 50 > 父节点 30，交换后数组为 [50, 30, 40]，parent=1，child=3
  4. child=3不小于n=3，循环终止，调整完成，结果为 [50, 30, 40]，满足大根堆性质
删除堆顶元素：
void HPPop(HP* php)
{assert(!HPEmpty(php));// 0 php->size-1Swap(&php->arr[0], &php->arr[php->size - 1]);--php->size;//向下调整AdjustDown(php->arr, 0, php->size);
}
  • 时间复杂度：O (log n)，主要由AdjustDown操作决定
  • 空间复杂度：O (1)，仅使用常数级额外空间
获取堆顶元素
//取堆顶数据
HPDataType HPTop(HP* php)
{assert(!HPEmpty(php));return php->arr[0];
}
堆的销毁
void HPDestroy(HP* php)
{if (php->arr)free(php->arr);php->arr = NULL;php->size = php->capacity = 0;
}

测试代码（堆排序---向下调整法建堆）

void arrPrint(int* arr, int n)
{for (int i = 0; i < n; i++){printf("%d ", arr[i]);}printf("\n");
}
void BubbleSort(int* arr, int n)
{for (int i = 0; i < n; i++){for (int j = 0; j < n - i - 1; j++){if (arr[j] > arr[j + 1]){Swap(&arr[j], &arr[j + 1]);}}}
}//堆排序
void HeapSort1(int* arr, int n)
{HP hp; //——————借助数据结构堆来实现堆排序HPInit(&hp);for (int i = 0; i < n; i++){HPPush(&hp, arr[i]);}int i = 0;while (!HPEmpty(&hp)){int top = HPTop(&hp);arr[i++] = top;HPPop(&hp);}HPDestroy(&hp);
}void HeapSort(int* arr, int n)
{//建堆——向下调整算法建堆for (int i = (n - 1 - 1) / 2; i >= 0; i--){AdjustDown(arr, i, n);}//堆排序int end = n - 1;while (end > 0){Swap(&arr[0], &arr[end]);AdjustDown(arr, 0, end);end--;}}void test01()
{HP hp;HPInit(&hp);HPPush(&hp, 56);HPPush(&hp, 10);HPPush(&hp, 15);HPPush(&hp, 30);//HPPush(&hp, 70);//HPPush(&hp, 25);HPPrint(&hp);HPPop(&hp);HPPrint(&hp);HPPop(&hp);HPPrint(&hp);HPPop(&hp);HPPrint(&hp);HPPop(&hp);HPPrint(&hp);HPDestroy(&hp);
}void test02()
{HP hp;HPInit(&hp);HPPush(&hp, 56);HPPush(&hp, 10);HPPush(&hp, 15);HPPush(&hp, 30);HPPrint(&hp);while (!HPEmpty(&hp)){int top = HPTop(&hp);printf("%d ", top);HPPop(&hp);}HPDestroy(&hp);
}int main()
{//test01();//test02();int arr[6] = { 19,15,20,17,13,10 };printf("排序之前：");arrPrint(arr, 6);//堆排序HeapSort(arr, 6);printf("排序之后：");arrPrint(arr, 6);return 0;
}

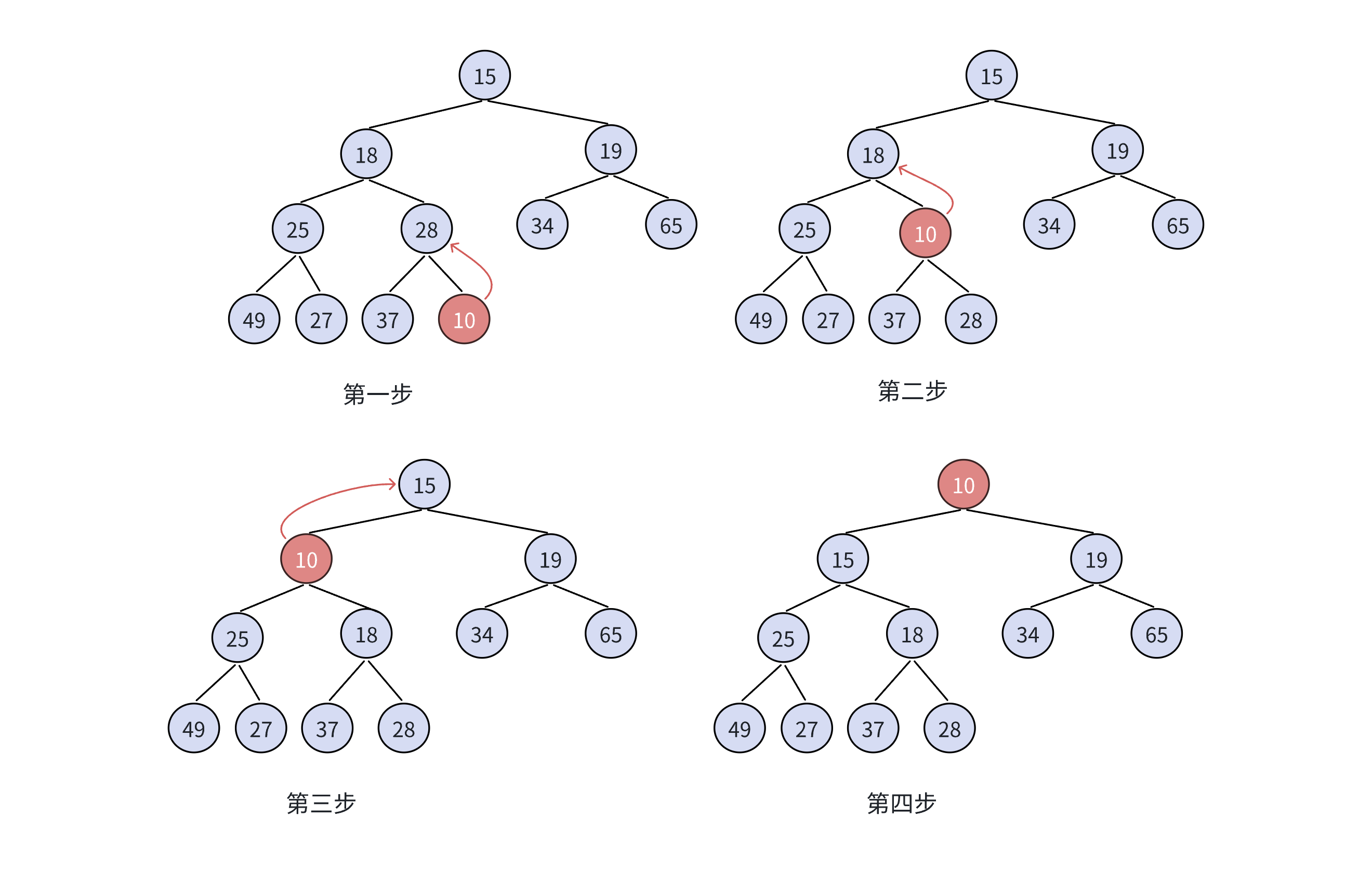
向上调整法建堆

将元素逐个插入堆中，每次插入后通过 “向上调整” 操作，确保新元素与父节点的关系符合堆的性质（最小堆中父节点值小于等于子节点值；最大堆中父节点值大于等于子节点值）。

步骤：

  1. 插入新元素：将新元素暂时放在堆的末尾（数组的最后一个位置）。
  2. 向上调整：比较新元素与其父节点的值，若不符合堆的性质（如最大堆中，新元素 > 父节点），则交换两者位置。
  3. 重复调整：继续将新元素与其新的父节点比较，直到新元素的父节点符合堆的性质，或新元素成为根节点（此时无法再向上调整）。

代码实现（完整）：

#include <stdio.h>// 交换两个元素
void Swap(int* a, int* b) {int temp = *a;*a = *b;*b = temp;
}// 向上调整算法（用于建堆）
// 假设构建的是最大堆
void AdjustUp(int* arr, int child) {int parent = (child - 1) / 2;// 当子节点索引大于0且子节点值大于父节点值时，需要调整while (child > 0) {if (arr[child] > arr[parent]) {Swap(&arr[child], &arr[parent]);child = parent;parent = (child - 1) / 2;} else {// 符合最大堆性质，无需继续调整break;}}
}// 向下调整算法（用于堆排序过程中维持堆性质）
// 假设构建的是最大堆
void AdjustDown(int* arr, int parent, int n) {int child = 2 * parent + 1; // 左孩子索引while (child < n) {// 选择左右孩子中值较大的那个if (child + 1 < n && arr[child + 1] > arr[child]) {child++;}// 如果父节点值小于子节点值，交换它们if (arr[parent] < arr[child]) {Swap(&arr[parent], &arr[child]);parent = child;child = 2 * parent + 1;} else {// 符合最大堆性质，无需继续调整break;}}
}// 堆排序函数
void HeapSort(int* arr, int n) {if (arr == NULL || n <= 1) {return; // 空数组或只有一个元素无需排序}// 建堆----向上调整法建堆for (int i = 0; i < n; i++) {AdjustUp(arr, i);}// 堆排序int end = n - 1;while (end > 0) {// 将堆顶元素（最大值）与末尾元素交换Swap(&arr[0], &arr[end]);// 调整剩余元素为最大堆AdjustDown(arr, 0, end);end--;}
}// 测试函数
int main() {int arr[] = {3, 1, 4, 1, 5, 9, 2, 6};int n = sizeof(arr) / sizeof(arr[0]);printf("排序前: ");for (int i = 0; i < n; i++) {printf("%d ", arr[i]);}printf("\n");HeapSort(arr, n);printf("排序后: ");for (int i = 0; i < n; i++) {printf("%d ", arr[i]);}printf("\n");return 0;
}

改变点：

向上向下建堆方法时间复杂度

向下调整法

相关计算：

①T (h) = 2 0 ∗ (h − 1) + 2 1 ∗ (h − 2) + 2 2 ∗ (h − 3) + 2 3 ∗ (h − 4) + .. + 2 h−3 ∗ 2 + 2 h−2 ∗ 1
② 2 ∗ T (h) = 2 1 ∗ (h − 1) + 2 2 ∗ (h − 2) + 2 3 ∗ (h − 3) + 2 4 ∗ (h − 4) + ... + 2 h−2 ∗ 2 + 2 h−1 ∗ 1
② ⼀ ① 错位相减：
T (h) = 1 − h + 2 1 + 2 2 + 2 3 + 2 4 + .. + 2 h−2 + 2 h−1T (h) = 2 0 + 2 1 + 2 2 + 2 3 + 2 4 + . + 2 h−2 + 2 h−1 − h
T (h) = 2 h − 1 − h
根据⼆叉树的性质： n = 2 h − 1 和 h = log2 (n + 1)
T (n) = n − log2 (n + 1) ≈ n
则向下调整法时间复杂度为o（n）

向上调整法

先将元素插⼊到堆的末尾,即最后⼀个孩子之后
插⼊之后如果堆的性质遭到破坏，将新插⼊结点顺着其双双亲往上调整到合适位置即可

第1层， 2^ 0 个结点，需要向上移动0层
第2层， 2 ^1 个结点，需要向上移动1层
第3层， 2 ^2 个结点，需要向上移动2层
第4层， 2 ^3 个结点，需要向上移动3层
......
第h层， 2 ^(h−1) 个结点，需要向上移动h-1层
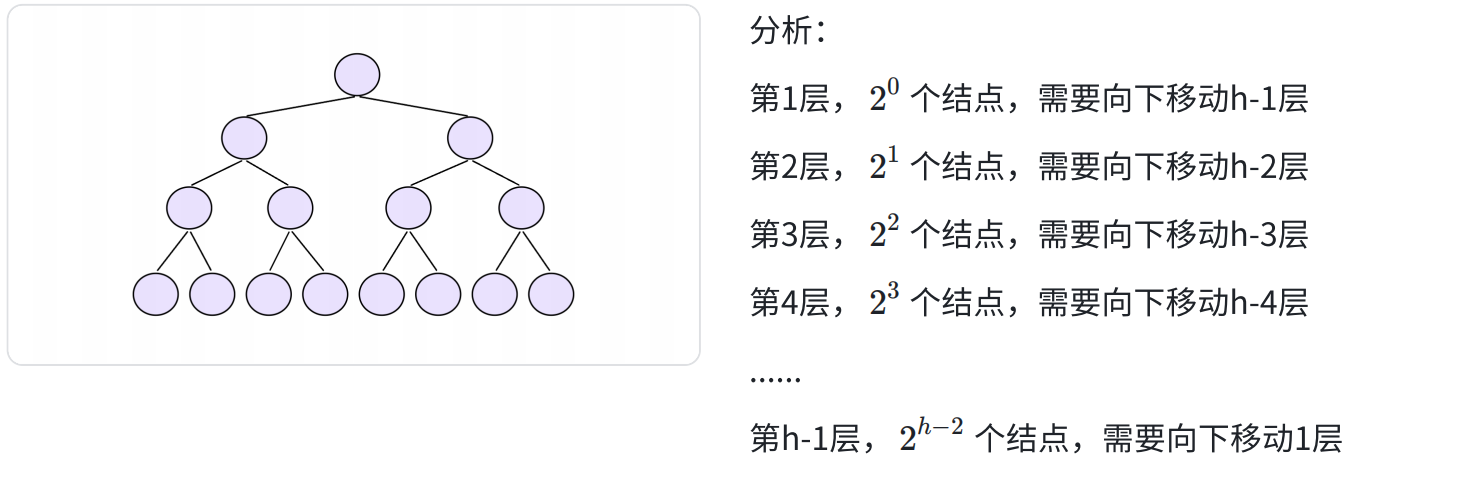
相关计算：
向上调整算法建堆时间复杂度为： O(n ∗ log2 n)

http://www.dtcms.com/a/330438.html

相关文章：

  • 18.14 全量微调实战手册：7大核心配置提升工业级模型训练效率
  • 阿里云RDS SQL Server实例之间数据库迁移方案
  • 通信算法之313：FPGA中实现滑动相关消耗DSP资源及7045/7035的乘法器资源
  • 工具栏扩展应用接入说明
  • React和Vue
  • Webpack Plugin 深度解析：从原理到实战开发指南
  • 使用AI编程自动实现自动化操作
  • Java 设计模式-组合模式
  • python的艺术品收藏管理系统
  • 数学建模层次分析法（AHP）笔记
  • C++入门自学Day11-- List类型的自实现
  • 2025天府杯数学建模B题分析
  • Vite 为什么比 Webpack 快？原理深度分析
  • Mac 新电脑安装cocoapods报错ruby版本过低
  • 一周学会Matplotlib3 Python 数据可视化-绘制面积图(Area)
  • 如何用aiohttp实现每秒千次的网页抓取
  • 机器视觉的磁芯定位贴合应用
  • PHP现代化全栈开发：实时应用与WebSockets实践
  • JVM字节码文件结构
  • PHP持久连接与普通连接的区别
  • 【大模型私有化部署】实战部分：Ollama 部署教程
  • 云蝠智能 VoiceAgent：重构物流售后场景的智能化引擎
  • Lua语言程序设计2：函数、输入输出、控制结构
  • 在CentOS系统中怎么查看Apache日志文件
  • Morph Studio-一站式AI视频创作平台
  • 亚马逊品牌权力重构：第三方卖家崛起下的竞争生态与系统性应对框架
  • AI引擎重构数据安全：下一代分类分级平台的三大技术跃迁
  • 从概率填充到置信度校准：GPT-5如何从底层重构AI的“诚实”机制
  • 深入解析 Chrome UI 布局配置的设计思想与实现机制
  • 快速搭建python HTTP Server测试环境