当前位置： 首页 > news >正文

红黑树的特性与实现

news 2025/8/14 17:06:46

在数据结构领域，二叉搜索树（BST）凭借 O (log n) 的平均时间复杂度成为查找、插入和删除操作的优选结构。但它有个致命缺陷：当输入数据有序时，会退化为链表，时间复杂度骤降至 O (n)。为解决这一问题，计算机科学家设计了多种自平衡二叉搜索树，红黑树（Red-Black Tree）便是其中应用最广泛的一种。它通过巧妙的着色规则和有限的旋转操作，在保证平衡的同时将维护成本降到最低，成为 STL 容器、Linux 内核等工业级系统的核心数据结构。本文将从底层原理到工程实践，全面剖析红黑树的工作机制。

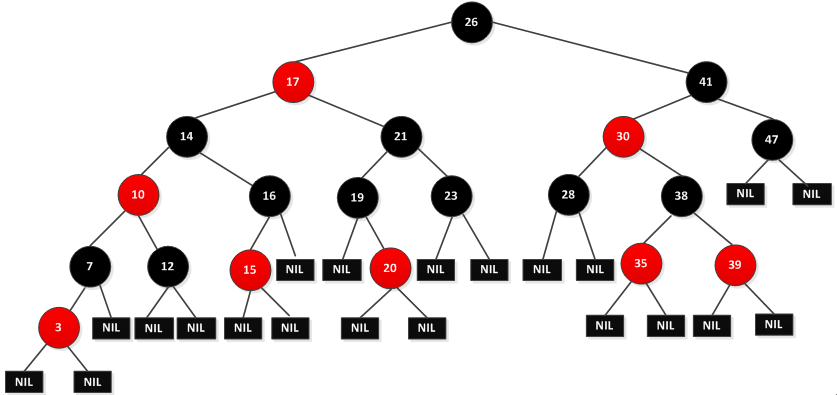
一、红黑树的核心特性与平衡原理

红黑树是一种自平衡二叉搜索树，其每个节点除了存储键值、左右子节点和父节点指针外，还额外包含一个颜色属性（红色或黑色）。通过严格遵循以下 5 条性质，红黑树实现了结构平衡：

  1. 颜色约束：每个节点要么是红色，要么是黑色。
  2. 根节点规则：根节点必须是黑色。
  3. 叶子节点规则：所有叶子节点（NIL 节点，即空节点）都是黑色。
  4. 连续红色禁止：如果一个节点是红色，则它的两个子节点必须是黑色（不存在连续的红色节点）。
  5. 黑色平衡规则：从任意节点到其所有后代叶子节点的路径中，包含的黑色节点数量相同（称为 "黑高"）。

平衡原理深度解析

这些特性共同构建了红黑树的 "平衡能力"：

  • 性质 4 避免了 "红色链" 的无限延伸，限制了树的倾斜程度；
  • 性质 5 保证了所有路径的 "黑高" 一致，而红色节点仅能穿插在黑色节点之间；
  • 由此可推导出关键结论：红黑树中最长路径的长度不会超过最短路径的 2 倍（最短路径全为黑色节点，最长路径为黑红交替）。

这一结论直接确保了红黑树的高度始终为 O (log n)，从而保证了所有操作的最坏时间复杂度为 O (log n)。

二、红黑树的节点结构与基础定义

2.1 节点结构设计

红黑树的节点需要存储 5 类信息：键值、颜色、左子节点、右子节点和父节点。为简化边界条件处理（如空节点的颜色判断），通常将所有空节点统一指向一个哨兵节点（NIL 节点），该节点永久为黑色，且左右子节点和父节点均指向自身。

enum Color { RED, BLACK };// 节点结构定义
struct Node {int key;          // 键值Color color;      // 节点颜色Node *left;       // 左子节点Node *right;      // 右子节点Node *parent;     // 父节点// 构造函数：新节点默认红色（插入时优化）Node(int k) : key(k), color(RED), left(nullptr), right(nullptr), parent(nullptr) {}
};// 哨兵节点定义（全局唯一）
Node *NIL_NODE = new Node(0);
NIL_NODE->color = BLACK;
NIL_NODE->left = NIL_NODE;
NIL_NODE->right = NIL_NODE;
NIL_NODE->parent = NIL_NODE;

2.2 关键设计细节

  • 哨兵节点的作用：将所有空指针替换为 NIL_NODE，避免在操作中频繁判断nullptr，统一边界处理逻辑；
  • 新节点默认红色：插入红色节点仅可能违反性质 4（连续红色），而插入黑色节点会直接违反性质 5（黑高不一致），前者修复成本更低；
  • 父节点指针的必要性：红黑树的旋转和修复操作需要回溯到祖先节点，必须通过父指针实现向上遍历。

三、红黑树的核心操作：插入与修复

3.1 插入流程

红黑树的插入操作分为两步：

  1. 按 BST 规则插入：找到合适位置插入新节点（默认红色）；
  2. 修复红黑树性质：通过旋转和变色消除对红黑树性质的破坏。
插入核心代码（BST 部分
void insert(Node *&root, int key) {Node *z = new Node(key);Node *y = NIL_NODE;  // 记录x的父节点Node *x = root;// 查找插入位置while (x != NIL_NODE) {y = x;if (z->key < x->key) {x = x->left;} else {x = x->right;}}// 确定新节点的父节点z->parent = y;if (y == NIL_NODE) {root = z;  // 树为空，新节点成为根} else if (z->key < y->key) {y->left = z;} else {y->right = z;}// 初始化新节点的子节点为哨兵z->left = NIL_NODE;z->right = NIL_NODE;z->color = RED;  // 新节点默认红色// 修复红黑树性质insertFixup(root, z);
}

3.2 插入后的修复操作（insertFixup）

插入红色节点后，可能违反的性质为：

  • 性质 2（根节点为红色）：仅当插入的是第一个节点时可能发生；
  • 性质 4（连续红色节点）：当父节点为红色时发生。

修复过程通过循环处理，直到上述性质均被满足。根据 "叔节点"（父节点的兄弟节点）的颜色，分为 3 种情况：

情况 1：叔节点为红色
  • 场景：新节点（z）的父节点（p）为红色，叔节点（u）为红色；
  • 破坏性质：仅可能违反性质 4（连续红色）；
  • 修复逻辑：
    1. 将父节点（p）和叔节点（u）改为黑色；
    2. 将祖父节点（g）改为红色；
    3. 令 z = g，继续向上修复（祖父节点可能与它的父节点形成连续红色）。
// 情况1：叔节点为红色
case 1:z->parent->parent->left->color = BLACK;  // 叔节点变黑z->parent->parent->right->color = BLACK; // 父节点变黑z->parent->parent->color = RED;          // 祖父节点变红z = z->parent->parent;                   // 向上追溯break;
情况 2：叔节点为黑色，且新节点是右孩子
  • 场景：父节点（p）为红色，叔节点（u）为黑色，z 是右孩子；
  • 破坏性质：性质 4（连续红色）；
  • 修复逻辑：
    1. 对父节点（p）执行左旋，将 z 转为左孩子；
    2. 转化为情况 3 处理（统一修复逻辑）。
// 情况2：叔节点为黑色，z是右孩子
case 2:z = z->parent;              // z指向父节点leftRotate(root, z);        // 左旋父节点// 转化为情况3
情况 3：叔节点为黑色，且新节点是左孩子
  • 场景：父节点（p）为红色，叔节点（u）为黑色，z 是左孩子；
  • 破坏性质：性质 4（连续红色）；
  • 修复逻辑：
    1. 对祖父节点（g）执行右旋；
    2. 交换父节点（p）和祖父节点（g）的颜色；
    3. 修复完成（无需继续向上追溯）。
// 情况3：叔节点为黑色，z是左孩子
case 3:z->parent->color = BLACK;   // 父节点变黑z->parent->parent->color = RED;  // 祖父节点变红rightRotate(root, z->parent->parent);  // 右旋祖父节点z = root;  // 退出循环break;

3.3 旋转操作的实现

旋转是红黑树维护平衡的核心手段，分为左旋和右旋，作用是改变节点间的父子关系而不破坏 BST 性质。

左旋操作（leftRotate）
void leftRotate(Node *&root, Node *x) {Node *y = x->right;  // y是x的右子节点x->right = y->left;  // 将y的左子树转为x的右子树if (y->left != NIL_NODE) {y->left->parent = x;  // 更新y左子树的父节点}y->parent = x->parent;  // 更新y的父节点// 处理x是根节点的情况if (x->parent == NIL_NODE) {root = y;} else if (x == x->parent->left) {x->parent->left = y;  // x是左孩子时，y替代x的位置} else {x->parent->right = y; // x是右孩子时，y替代x的位置}y->left = x;  // x成为y的左孩子x->parent = y;  // 更新x的父节点
}
右旋操作（rightRotate）

右旋与左旋对称，核心是将左子节点提升为父节点，此处不再赘述。

四、红黑树的删除操作与修复

删除操作是红黑树中最复杂的部分，核心挑战是如何在删除节点后维持红黑树的 5 条性质。删除流程分为 3 步：

  1. 按 BST 规则删除节点：找到待删除节点，根据节点的子节点数量（0、1、2）执行不同删除逻辑；
  2. 记录关键信息：跟踪 "替代节点"（实际被移除的节点）及其原始颜色；
  3. 修复红黑树性质：若删除的是黑色节点，需通过修复流程恢复平衡。

4.1 BST 删除逻辑

  • 叶子节点（无孩子）：直接删除；
  • 单孩子节点：用子节点替代该节点；
  • 双孩子节点：找到中序后继（右子树最小节点），复制其值到当前节点，再删除后继节点（转化为前两种情况）。

4.2 删除后的修复操作（deleteFixup）

删除节点后，若被删除节点是黑色，会破坏性质 5（黑高不一致），此时需要通过 "双重黑色" 标记来修复。"双重黑色" 表示该路径上缺少一个黑色节点，需要通过以下 4 种情况消除：

情况 1：兄弟节点为红色
  • 场景：当前节点（x）为双重黑色，兄弟节点（s）为红色；
  • 修复逻辑：
    1. 将兄弟节点（s）改为黑色，父节点（p）改为红色；
    2. 对父节点（p）执行左旋；
    3. 转化为其他情况（兄弟节点变为黑色）。
情况 2：兄弟节点为黑色，且兄弟的两个孩子均为黑色
  • 场景：x 为双重黑色，s 为黑色，s 的左右孩子均为黑色；
  • 修复逻辑：
    1. 将兄弟节点（s）改为红色；
    2. 令 x = p（将双重黑色上移）；
    3. 继续向上修复。
情况 3：兄弟节点为黑色，左孩子红色，右孩子黑色
  • 场景：x 为双重黑色，s 为黑色，s 的左孩子红、右孩子黑；
  • 修复逻辑：
    1. 将 s 的左孩子改为黑色，s 改为红色；
    2. 对 s 执行右旋；
    3. 转化为情况 4。
情况 4：兄弟节点为黑色，右孩子为红色
  • 场景：x 为双重黑色，s 为黑色，s 的右孩子为红色；
  • 修复逻辑：
    1. 将 s 的颜色改为 p 的颜色；
    2. 将 p 改为黑色，s 的右孩子改为黑色；
    3. 对 p 执行左旋；
    4. 令 x = root（修复完成）。

4.3 修复操作的核心目标

  • 消除 "双重黑色" 标记，恢复路径上的黑高平衡；
  • 避免出现连续红色节点，维持性质 4；
  • 通过最少的旋转和变色操作完成修复，降低时间开销。

五、红黑树与 AVL 树的深度对比

特性红黑树AVL 树
平衡标准颜色规则 + 黑高平衡左右子树高度差≤1（严格平衡）
旋转次数插入最多 2 次，删除最多 3 次插入最多 2 次，删除可能 O (log n)
空间开销存储颜色（1bit）存储平衡因子（通常需 2-4bit）
查找性能平均 O (log n)，最坏 O (2log n)严格 O (log n)（高度更优）
插入 / 删除性能更优（旋转少）较差（严格平衡导致旋转频繁）
适用场景插入删除频繁的场景（如 STL 容器）查找频繁的场景（如数据库索引）

红黑树的工业级优势：在大多数实际场景中，红黑树的综合性能优于 AVL 树。虽然 AVL 树的高度更优，但红黑树的旋转操作更少，维护成本更低，尤其适合插入删除频繁的动态数据场景。

六、红黑树的实际应用场景

  1. C++ STL 容器：std::map、std::set、std::multimap等关联容器底层均采用红黑树实现，利用其 O (log n) 的插入、删除和查找性能；
  2. Linux 内核：
    • 进程调度：CFS（完全公平调度器）用红黑树管理进程运行队列，快速找到下一个待调度进程；
    • 虚拟内存管理：VM_area_struct 结构体用红黑树组织，高效管理内存区域；
  3. Java 集合框架：TreeMap、TreeSet底层基于红黑树，提供有序映射和集合功能；
  4. 数据库：部分数据库（如 MongoDB）的索引结构采用红黑树，平衡查询和更新性能；
  5. 编译器实现：语法分析阶段的符号表常用红黑树存储变量和函数信息，支持快速查找和插入。
http://www.dtcms.com/a/330335.html

相关文章：

  • 打靶日常-文件上传
  • 【Python】新手入门：什么是python运算符？python运算符有哪些种类？运算符优先级是怎么样的？
  • Go语言函数详解：从基础到高阶的行为逻辑构建
  • C5.4:光电器件
  • RagFlow启动源码说明
  • Linux framebuffer 编程入门：直接操作显存画图
  • Flutter权限管理三步曲：检查、申请、处理全攻略
  • 【超算】算力的精度，数据中心的划分标准与行业现状（国家超级计算机，企业万卡GPU集群）
  • 深入详解C语言的循环结构：while循环、do-while循环、for循环，结合实例，讲透C语言的循环结构
  • 关于linux软件编程4：目录IO和一些时间函数
  • PAT 1065 A+B and C (64bit)
  • 驱动开发系列62 - glBufferDataARB实现分析
  • Windows下cuda的安装和配置
  • BGP 笔记梳理
  • 110. 字符串接龙
  • 【Spring AI 1.0.0】Spring AI 1.0.0框架快速入门(6)——MCP Client（MCP客户端）
  • 最新Coze（扣子）智能体工作流：用Coze实现「图片生成-视频制作」全自动化，3分钟批量产出爆款内容
  • Docker网络命名空间隔离与VPS服务器环境的连通性测试方法解析
  • kali linux 2025.2配置局域网打印服务器惠普打印机HP1108p
  • MySQL查询表结构、表大小
  • 告别意外中断，iOS辅助工具按键精灵「异常停止重启脚本」功能介绍
  • ＜c1:C1DateTimePicker的日期时间控件，控制日期可以修改，时间不能修改，另外控制开始时间的最大值比结束时间小一天
  • git clone 支持在命令行临时设置proxy
  • 康托展开与逆康托展开
  • 词向量转化
  • RocketMQ 消息存储机制 CommitLog和ConsumerQu
  • 第八课：python的运算符
  • 从 VLA 到 VLM：低延迟RTSP|RTMP视频链路在多模态AI中的核心角色与工程实现
  • 论文分享 | Flashboom：一种声东击西攻击手段以致盲基于大语言模型的代码审计
  • 04-spring-手写spring-demo-aop0V1