LeetCode刷题记录----437.路径总和Ⅲ(medium)
2025/8/13
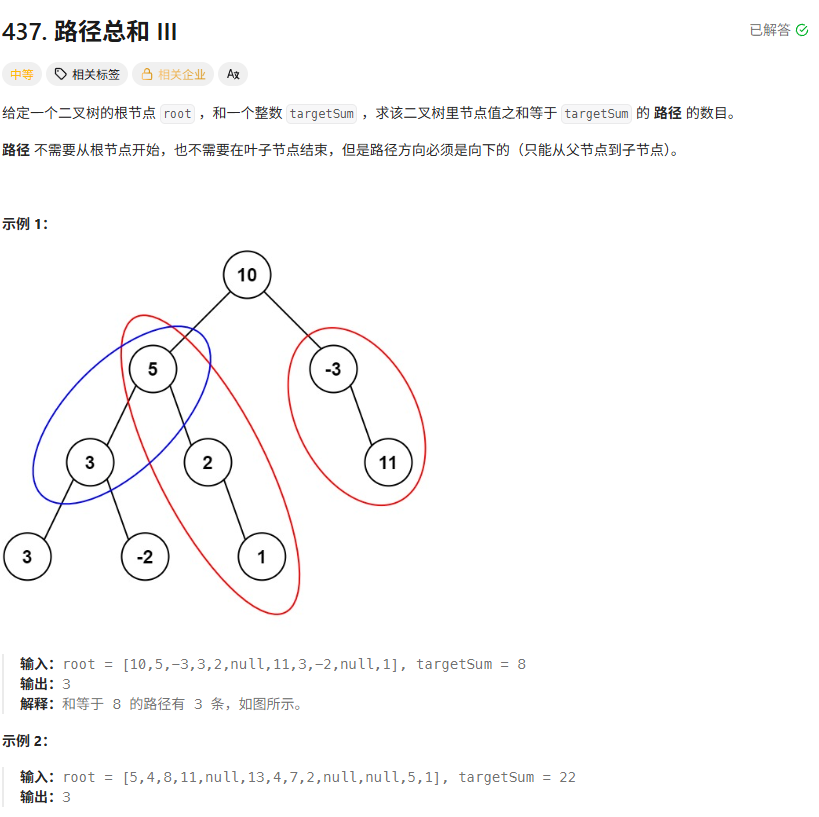
题目(medium):
我的思路:
很容易的可以想到的是把这颗树中所有的路径都求一次路径和,然后来判断有几条路径是满足题目的要求的。因此我们要考虑如何对所有的路径进行遍历。
首先路径肯定是由起点和终点组成的,那所有的路径肯定是所有的节点都会成为起点,而该节点作为根节点的子树中的节点也都会作为该节点的终点。
因此通过以上的分析我们可以知道:
①对每一个节点都要进行一次它作为根节点的子树遍历
②且这个子树遍历到的位置都是作为这个路径的终点
那还剩一个需要考虑的就是如何判断该路径的合法性:
①只要给每个作为终点遍历到的节点位置传入它这个节点需要的目标值即可(比如根节点是10,而目标值是8,现在遍历到了它的左孩子位置,我们自然希望左孩子的值是8-10 = -2,其他的节点以此类推)
综上可以知道算法步骤如下:
①传入树的根节点作为起点,并深度优先搜索来遍历它的所有子节点作为终点
②对于每个子节点判断他的值是否等于(根节点值-目标值),若等于则答案值+1
③在对树的根节点这样检索完毕之后,再把它的左右子树按步骤一二继续进行检索判断
具体代码如下:
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:def pathSum(self, root: Optional[TreeNode], targetSum: int) -> int:#深搜遍历每一种可能#该函数用于求以当前根节点作为路径起始点的时候得到的目标路径的数量def rootSum(root:Optional[TreeNode], targetSum:int) -> int:if root is None:return 0#先判断根节点自己满不满足目标值res = 0if root.val == targetSum:res += 1#然后判断根节点的左右子树中满足的个数res += rootSum(root.left, targetSum - root.val)res += rootSum(root.right, targetSum - root.val)return resif root is None:return 0res = rootSum(root, targetSum) #以根节点作为起始节点满足的路径数res += self.pathSum(root.left, targetSum) #求左子树中满足的路径数res += self.pathSum(root.right, targetSum) #求右子树中满足的路径数return res
时间复杂度:O()【对于每个节点都要作为起点去检索一次它作为根节点的子树】
空间复杂度:O(N)
优化思路:
显然,时间复杂度这么高的原因在于其中存在着很多重复的计算。从上面的方法我们也可以感觉到,它似乎和N数之和这种题目有些相似。而N数之和我们是可以用前缀和的方式来解决,对于这个题目当然也是可以的。这里的前缀和我们定义为:从树的根节点到该节点的值的和
即我们如何快速判断当前节点作为终点的时候,有没有适配的节点作为起点和它组成路径呢?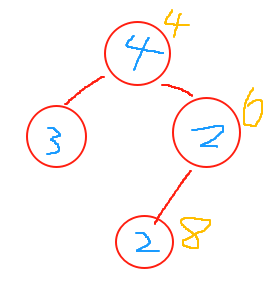
以该图为例子,蓝色的字表示节点的值,黄色的字表示从根节点到这个节点的路径的路径和。我们可以知道4→2→2这条路径的路径和是8,那如果我想要知道2→2这条路径的路径和该怎么求呢?那直接通过8-4 = 4 即可求得。此时我们的得知一个节点的前缀和 - 另一个节点的前缀和 = 路径和
那我们要判断是否存在有效路径只要通过终点节点的前缀和 - 起点节点的父节点的前缀和 ?= targetNum即可。假设targetNum == 4 , 则我们直接通过逆向思维可以知道 终点节点的前缀和 - targetNum == 起点节点的父节点的前缀和。这里正好 8(终点前缀和) - 4(目标值) == 4,而正好又存在一个前缀和为4的节点(图中为根节点),因此这里存在一条路径和为4的路径。
因此我们会进行如下的操作:
①声明一个哈希表(没有值的键对应的值为0),用于记录某个路径和的值有几条路径对应
②传入当前节点位置的路径和,然后让路径和的值加上当前节点的值求得当前节点的前缀和
③用当前节点的前缀和 - 目标值得到的值去哈希表中搜素这个前缀和的节点有几个,并加在结果值上
④把哈希表以当前节点的前缀和作为键的值+1
⑤递归计算左右子树中的有效路径数并+在结果值上
⑥然后把哈希表以当前节点的前缀和作为键的值-1【因为此时说明当前节点作为根节点的树的所有前缀和都已经应用完毕,移除出去避免影响其他树的路径和计算】
具体代码如下:
class Solution:def pathSum(self, root: Optional[TreeNode], targetSum: int) -> int:prefix = collections.defaultdict(int)prefix[0] = 1def dfs(root, curr):if root is None:return 0#计算到该节点为终点的路径的前缀和curr += root.valres = 0res += prefix[curr - targetSum] #判断是否有满足条件的起始节点的前缀和#更新当前节点作为起始节点的前缀和prefix[curr] += 1#然后再得到左右子树的有效路径数res += dfs(root.left, curr)res += dfs(root.right, curr)#到这里说明这个根节点作为起点进行有效路径检索的前缀和已经结束#需要把他移除出去避免影响另一边子树的路径判断prefix[curr] -= 1return resreturn dfs(root, 0)时间复杂度:O(N)
空间复杂度:O(N)
总结:
①对求所有的东西中哪些东西是合法的这种问题可以考虑暴力地把每一个东西都具体求出来并判断
②对于有关N个数相乘或者相加的问题的合法性判断,可以考虑使用前缀和和哈希表配合来对暴力算法进行优化
