[Robotics_py] 机器人运动模型 | `update`函数 | 微积分矩阵
第三章:机器人运动模型
欢迎回来,未来的机器人专家~
在第一章:机器人状态/位姿中,我们学习了机器人如何跟踪自身状态:位置、朝向和速度。接着在第二章:环境表征(栅格地图)中,我们探索了机器人如何通过栅格地图理解周围世界。
现在,机器人已经知道自身位置并拥有环境地图。
但它如何真正实现从一处移动到另一处?当它决定加速或转向时,如何预测自身位置?
这正是机器人运动模型的核心作用!
什么是机器人运动模型?
可将机器人运动模型视为机器人的"物理引擎"。
这是一组数学规则,描述机器人基于接收的"指令"或"控制输入"随时间推移如何改变其状态(即第一章提到的x、y、yaw和v)。
为何这个"物理引擎"如此重要?
假设我们试图玩一个预测抛球落点的游戏,需要理解重力、抛掷力度和方向。机器人运动与之相似!运动模型使机器人能够:
- 预测未来位置:"若车轮如此转向并施加特定动力,下一秒钟我会处于何处?"这对
路径规划和避障至关重要。 - 模拟运动:运行虚拟机器人以测试算法,无需实体机器人。
- 估计自身位置:正如我们将在第四章:定位滤波器所见,这些预测是
帮助机器人确定*实际*精确位置的关键要素,即使传感器存在噪声。
本质上,运动模型是机器人规划与理解自身运动的核心。
运动模型的关键概念
要理解机器人运动机制,需考虑以下要素:
| 概念 | 描述 | 类比 |
|---|---|---|
| 当前状态 | 机器人此刻的位置(x、y、yaw、v)。 | 地图上的当前坐标。 |
| 控制输入 | 机器人执行的动作(如加速度、转向角、轮速)。 | 踩油门踏板力度与方向盘转动角度。 |
时间步长(dt) | 用于计算运动的极小时段。 | 逐帧观看电影。 |
| 下一状态 | 执行dt时长动作后的新x、y、yaw、v。 | 移动瞬间后的新位置。 |
运动模型本质上是: 当前状态和控制输入结合时间步长,输出下一状态。
如何使用简单运动模型(update函数)
其实我们已在第一章见过简单运动模型——展示机器人状态变化的update函数。
让我们重温这个PythonRobotics中众多运动模型的核心。
该模型常被称为运动学自行车模型或**独轮车模型**,因其将
类车机器人简化为两轮(前轮与后轮),不考虑摩擦或引擎动力等复杂力。
它适用于低速路径规划。
以下是PathTracking/pure_pursuit/pure_pursuit.py &PathPlanning/ModelPredictiveTrajectoryGenerator/motion_model.py中update函数的简化版:
import math
import numpy as np # 常用于数学函数或数组操作
from utils.angle import angle_mod # 帮助将角度保持在合理范围内 WB = 2.9 # 车辆轴距(前后轮间距,单位:米)
dt = 0.1 # 时间步长(秒),例如每0.1秒更新一次 class State: def __init__(self, x=0.0, y=0.0, yaw=0.0, v=0.0): self.x = x self.y = y self.yaw = yaw self.v = v def update_motion_model(state, acceleration, steering_angle): # 1. 更新速度(加速/减速) state.v += acceleration * dt # 2. 更新位置(前进/后退) state.x += state.v * math.cos(state.yaw) * dt state.y += state.v * math.sin(state.yaw) * dt # 3. 更新朝向(转向) # 'yaw'变化基于当前速度、轴距和转向角 state.yaw += state.v / WB * math.tan(steering_angle) * dt state.yaw = angle_mod(state.yaw) # 保持yaw在-π到π之间 return state
代码解析:
update_motion_model(state, acceleration, steering_angle):该函数接收机器人state(当前x, y, yaw, v)、acceleration指令(速度变化量)和steering_angle指令(前轮转向角度)。state.v += acceleration * dt:更新速度。若acceleration为正则加速,为负则减速。state.x += state.v * math.cos(state.yaw) * dt:X坐标变化。state.v * dt给出dt时间内的移动距离,math.cos(state.yaw)和math.sin(state.yaw)将前进运动分解为X、Y轴变化,考虑机器人朝向。state.yaw += state.v / WB * math.tan(steering_angle) * dt:转向核心逻辑。yaw变化取决于移动速度、轴距和转向角度。state.yaw = angle_mod(state.yaw):来自utils/angle.py的辅助函数,保持yaw在-π到π弧度(-180°到180°)间,避免无限增长。
示例:机器人运动仿真
观察机器人多步运动:
# 创建初始状态
initial_state = State(x=0.0, y=0.0, yaw=math.radians(0), v=0.0)
print(f"初始状态: X={initial_state.x:.2f}, Y={initial_state.y:.2f}, " f"Yaw={math.degrees(initial_state.yaw):.2f}°, V={initial_state.v:.2f} m/s") # 3秒仿真循环
current_time = 0.0
total_sim_time = 3.0
print("\n--- 运动仿真 ---") while current_time < total_sim_time: # 施加恒定加速度和小转向角 accel_cmd = 0.5 # m/s²(加速) steer_cmd = math.radians(5.0) # 5°(温和右转) # 更新机器人状态 current_state = update_motion_model(initial_state, accel_cmd, steer_cmd) current_time += dt # 演示时每秒打印一次 if int(current_time * 10) % 10 == 0: print(f"时间: {current_time:.1f}s | " f"X={current_state.x:.2f}, Y={current_state.y:.2f}, " f"Yaw={math.degrees(current_state.yaw):.2f}°, V={current_state.v:.2f} m/s") print(f"\n{total_sim_time:.1f}秒后最终状态:")
print(f"X={current_state.x:.2f}, Y={current_state.y:.2f}, " f"Yaw={math.degrees(current_state.yaw):.2f}°, V={current_state.v:.2f} m/s")
输出(近似值):
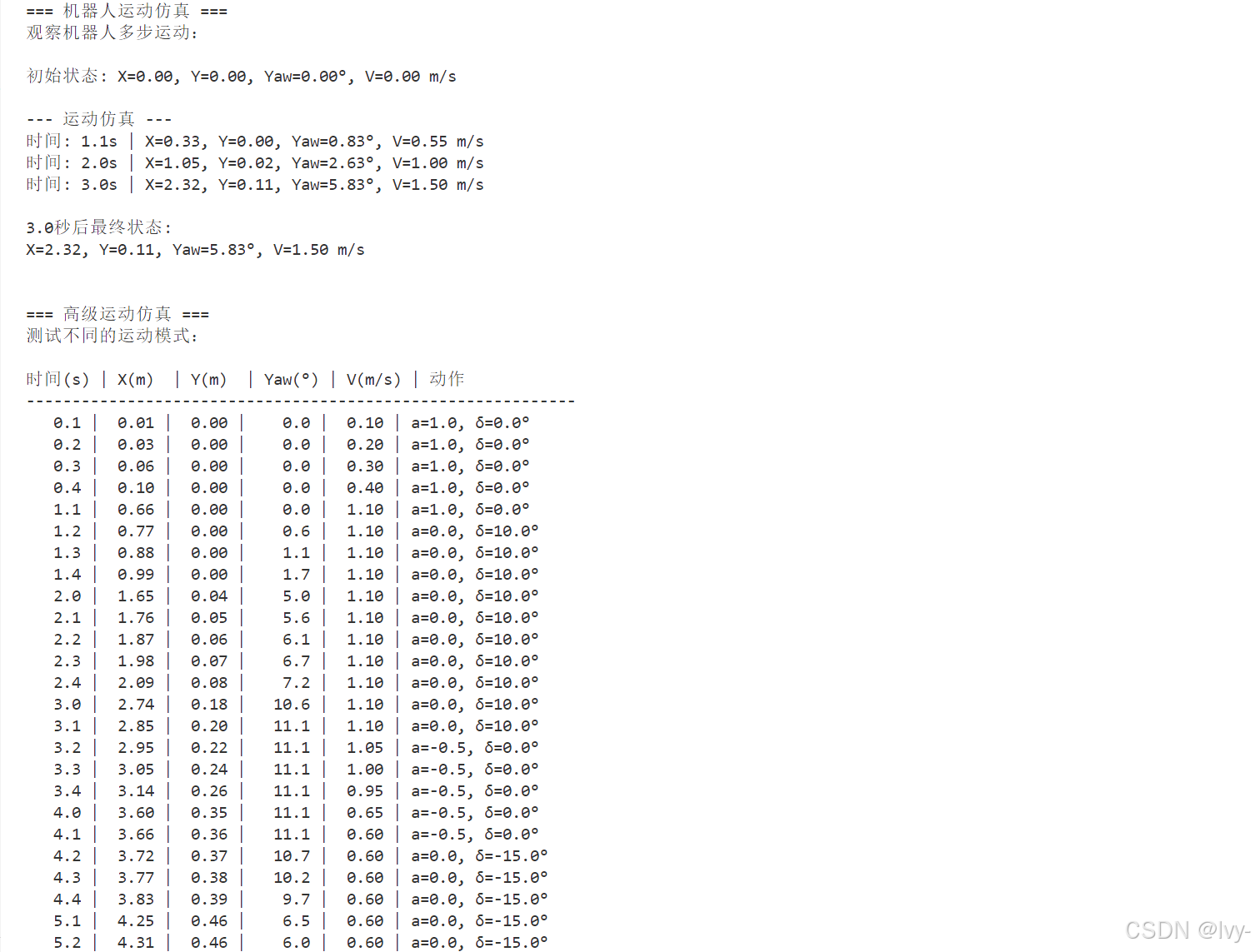
可见x、y、yaw和v随时间逐步变化。通过重复调用此update函数,我们能仿真机器人在环境中的路径。
运动模型内部工作原理
可视化运动模型在机器人思考流程中的作用:
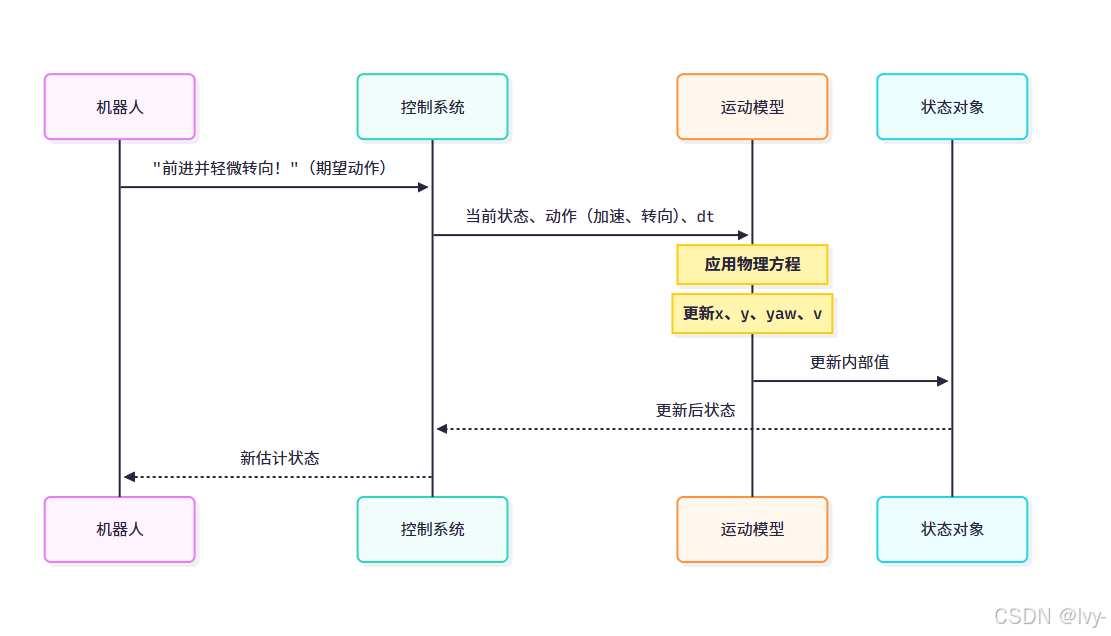
更新背后的数学原理
update_motion_model函数的方程基于基础微积分。当dt(时间步长)极小时,我们可近似计算变化量:
- X变化:
dx = v * cos(yaw) * dt - Y变化:
dy = v * sin(yaw) * dt - Yaw变化:
dyaw = (v / WB) * tan(steering_angle) * dt - 速度变化:
dv = acceleration * dt
新状态即旧状态加上这些微小变化:
new_x = old_x + dx
new_y = old_y + dy
new_yaw = old_yaw + dyaw
new_v = old_v + dv
这正是update_motion_model函数逐步计算的内容。
矩阵形式(高级模型)
部分运动模型(尤其用于扩展卡尔曼滤波器等高级滤波器)用矩阵表示这些方程。
初看可能复杂,但实质是相同关系的紧凑表达。
例如,在Localization/extended_kalman_filter/extended_kalman_filter.py中,motion_model函数如下:
# 摘自Localization/extended_kalman_filter/extended_kalman_filter.py def motion_model(x, u): # x是状态向量[x, y, yaw, v]' # u是控制输入向量[速度指令, 偏航率指令]' # DT是时间步长 # F矩阵描述当前状态(x)如何直接影响下一状态 F = np.array([[1.0, 0, 0, 0], [0, 1.0, 0, 0], [0, 0, 1.0, 0], [0, 0, 0, 0]]) # F[3,3]为0,因速度通过B*u改变 # B矩阵描述控制输入(u)如何影响状态变化 B = np.array([[DT * math.cos(x[2, 0]), 0], # 速度引起的x变化 [DT * math.sin(x[2, 0]), 0], # 速度引起的y变化 [0.0, DT], # 偏航率引起的yaw变化 [1.0, 0.0]]) # 加速度引起的速度变化 # 新状态为 F * 旧状态 + B * 控制输入 x = F @ x + B @ u # @表示矩阵乘法 return x
解析:
x作为列向量(垂直排列的数值列表:[x, y, yaw, v])。F矩阵表明在考虑控制输入前,“新x等于旧x”,其他状态同理。B矩阵添加控制输入引起的变化。例如,假设u[0,0]为速度v,DT * math.cos(x[2, 0])(x[2,0]即yaw角)计算v*dt*cos(yaw)对应的dx。
虽然数学形式不同,但结果一致:基于机器人动作预测其下一x、y、yaw和v。
PythonRobotics中的各类运动模型
根据算法或机器人类型,PythonRobotics使用不同运动学模型变体,核心思想始终如一:根据当前状态和控制输入预测下一状态。
项目代码库中的几个示例:
PathTracking/pure_pursuit/pure_pursuit.py:使用与所述update_motion_model相似的State.update方法,适用于类车机器人,特别追踪rear_x和rear_y(后轴位置),这对纯追踪算法很重要。PathPlanning/ModelPredictiveTrajectoryGenerator/motion_model.py:包含update函数和generate_trajectory函数,后者重复调用update以预测未来状态序列,生成完整轨迹,这对规划至关重要。PathTracking/cgmres_nmpc/cgmres_nmpc.py:使用differential_model函数计算瞬时变化率(dx、dy、dyaw、dv),通过积分(小dt步长累加)得到新状态,虽更复杂但仍基于相同运动学原理。
这些示例表明,尽管实现细节不同(如直接状态更新与微分方程、矩阵形式与简单方程),机器人运动模型的根本目的一致:
回答"若执行这些动作,机器人将处于何处?"
结语
本章解析了机器人运动模型这一关键概念。
我们了解到它是机器人的内部"物理引擎",基于当前状态和控制输入(如加速度和转向)预测未来状态(x、y、yaw、v)。我们探索了简单却强大的update函数,理解其 利用小dt步长仿真运动。
理解运动模型是机器人仿真、规划及定位的基础。
在下一章第四章:定位滤波器中,我们将看到这些预测如何与现实传感器数据结合,帮助机器人以更高精度确定真实位置与朝向。
下一章:定位滤波器
