【递归、搜索与回溯算法】综合练习

一、找出所有子集的异或总和再求和

题目描述：

思路讲解：
本道题需要我们根据一个数组 nums ，求出 nums 中每个子集的异或总和 ，计算并返回这些值相加之和，那么首先我们就要先解决找到全部子集的问题。

思路一：逐步选择元素，构建所有可能的子集，通过回溯法在每一步决定是否选择当前元素，最终生成所有不重复的子集。

思路二：按照子集的大小（即包含的元素个数）进行分类，然后分别找出每一类所有子集。

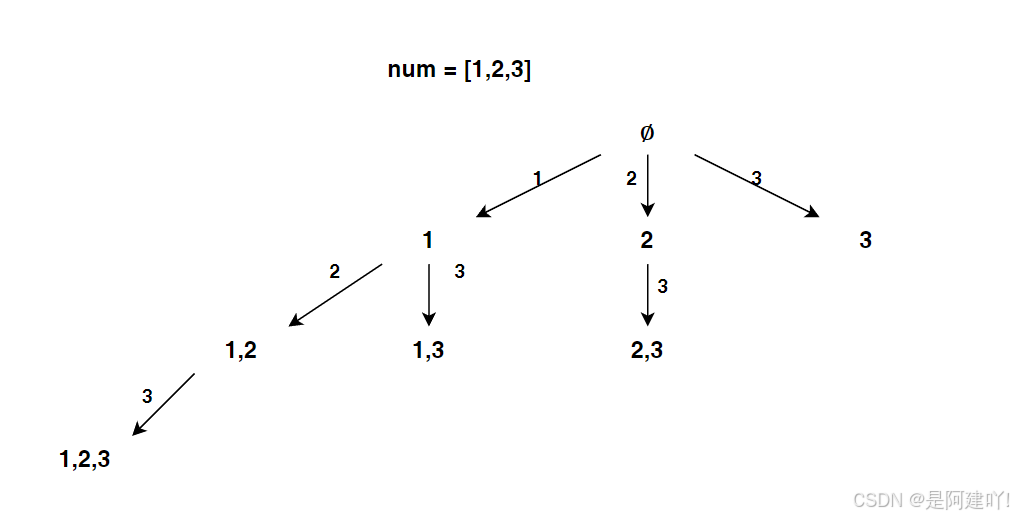
以下是思路二的具体思路：

• 全局变量：
  • cur：当前正在构建的子集中所有元素的异或结果
  • ans：存储所有子集的结果集
• 递归逻辑：
  • 空集（0 个元素）：
    • 初始调用时 cur=0（空集的异或总和为 0），首次进入递归函数即执行 ans += cur，将空集结果计入总和
  • 1 个元素的子集：
    • 从 pos=0 开始遍历，首次选择 nums[0] 时，cur 更新为 nums[0]，递归进入下一层后将该值加入 ans；同理，后续依次选择 nums[1]、nums[2] 等单个元素，生成所有 1 个元素的子集并累加异或结果
  • k 个元素的子集（k≥2）：
    • 递归过程中，通过 for 循环从 pos 开始选择元素，每次选择 nums[i] 后，cur 异或该元素，再递归探索从 i+1 开始的元素，形成包含 k 个元素的子集
  • 回溯实现元素个数的切换：
    • 每次递归返回后，通过 cur ^= nums[i] 撤销当前元素的选择，回到上一层状态，继续遍历下一个元素，切换到其他相同个数或更少个数元素的子集生成路径

编写代码：

class Solution {int ans = 0 , cur = 0;
public:void _subsetXORSum(vector<int>& nums , int pos) {ans += cur;for(int i = pos ; i < nums.size() ; i++){cur ^= nums[i];_subsetXORSum(nums,i + 1);cur ^= nums[i];}}int subsetXORSum(vector<int>& nums) {_subsetXORSum(nums,0);return ans;}
};

---

二、全排列 II

题目描述：

思路讲解：
本道题需要我们根据一个可包含重复数字的序列 nums ，按任意顺序 返回所有不重复的全排列，通过递归尝试所有可能的元素排列，在每一步选择一个未使用的元素加入当前排列（该元素不能是已经使用的重复数字），完成选择后回溯并尝试下一个元素，直到生成所有完整排列。以下是具体思路：

• 核心任务：
  • 数组含重复元素时，直接递归会生成重复排列，需通过排序 + 跳过重复元素的方式去重
• 全局变量：
  • path：当前正在构建的排列
  • isuse：记录元素是否已被使用
  • ans：存储所有完整排列的结果集
• 终止条件：
  • 当 path 的长度等于 nums 的长度时，说明已生成一个完整排列，将其加入 ans 并返回
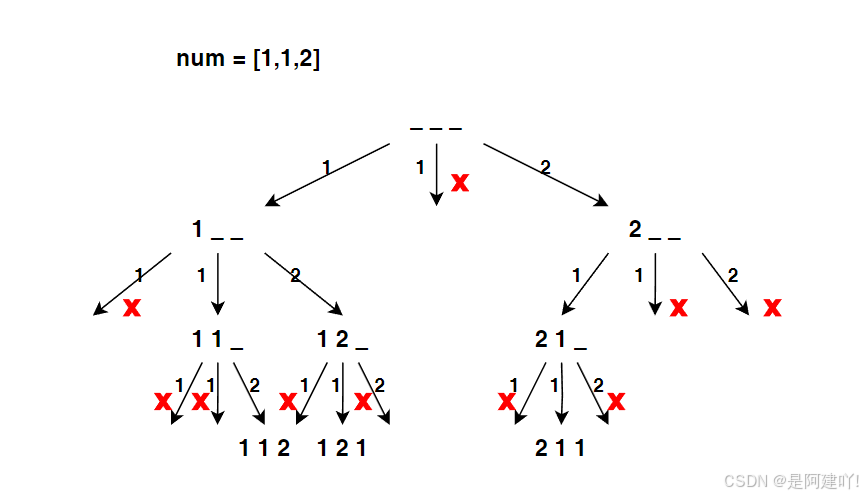
• 去重逻辑：
  • 先对 nums 排序，使重复元素相邻，为去重提供条件
  • 在遍历选择元素时，若当前元素与前一个元素相同，且前一个元素未被使用，则跳过当前元素
• 递归逻辑：
  • 遍历数组元素，若元素未被使用且不满足重复跳过条件：
    • 选择元素：将元素加入 path，标记 isuse[i] = true
    • 递归深入：继续构建下一个位置的元素
    • 回溯撤销：递归返回后，将元素从 path 中移除，标记 isuse[i] = false

编写代码：

class Solution {vector<vector<int>> ans;bool isuse[9];vector<int> path;int size;
public:void _permuteUnique(vector<int>& nums) {if(path.size() == nums.size()){ans.push_back(path);return;}for(int i = 0 ; i < size ; i++){if(isuse[i] == false && (i == 0 || (nums[i] != nums[i-1] || isuse[i-1] == true ))){path.push_back(nums[i]);isuse[i] = true;_permuteUnique(nums);isuse[i] = false;path.pop_back();}}}vector<vector<int>> permuteUnique(vector<int>& nums) {sort(nums.begin(),nums.end());size = nums.size();_permuteUnique(nums);return ans;}
};

---

三、电话号码的字母组合

题目描述：

思路讲解：
本道题需要我们给定一个仅包含数字 2-9 的字符串，返回所有它能表示的字母组合。我们可以通过回溯法，逐层拼接每个数字对应的字母，生成所有可能的组合。以下是具体思路：

• 建立映射关系：
  • 首先建立数字到对应字母的映射，便于根据输入数字快速获取可选字母
• 全局变量：
  • path：当前正在构建的字母组合
  • ans：存储所有完整组合的结果集
  • numTostr：数字到字母的映射表
• 终止条件：
  • 当 path 的长度等于 digits 的长度时，说明已处理完所有数字，将 path 加入 ans 并返回
• 递归逻辑：
  • 获取当前数字对应的字母串
  • 遍历该字母串中的每个字母：
    • 将字母加入 path 中，构建当前位置的组合
    • 递归处理下一个数字（pos + 1）
    • 从 path 中移除刚加入的字母，尝试下一个字母

编写代码：

class Solution {vector<string> numTostr = {"","","abc","def","ghi","jkl","mno","pqrs","tuv","wxyz"};string path;vector<string> ans;
public:void _letterCombinations(string& digits , int pos) {if(path.size() == digits.size()){ans.push_back(path);return;}string str = numTostr[digits[pos]-'0'];int cnt = str.size();for(int i = 0 ; i < cnt ; i++){path += str[i];_letterCombinations(digits,pos + 1);path.pop_back();}}vector<string> letterCombinations(string digits) {if(digits.size() == 0) return ans;_letterCombinations(digits,0);return ans;}
};

---

四、括号生成

题目描述：

思路讲解：
本道题需要我们根据数组n生成所有可能的并且有效的括号组合。那么我们需要先了解什么是有效的括号组合。

1. 左括号的数量 = 右括号的数量
2. 从头开始的任意子串中左括号的数量 >= 右括号的数量

根据这两个条件再对括号进行组合即可生成所以有效的括号组合，以下是具体思路：

• 全局变量：
  • path：当前正在构建的括号字符串
  • ans：存储所有有效组合的结果集
• 函数参数：
  • n：目标括号对数
  • left：当前已使用的左括号数量
  • right：当前已使用的右括号数量
• 终止条件：
  • 当右括号的数量等于n时，说明已生成一个有效组合，将其加入 ans 并返回
    递归逻辑：
  • 添加左括号：若 left < n（左括号未用完），则在 path 后加 ‘(’，递归时 left 加 1
  • 添加右括号：若 right < left（右括号数量小于左括号，确保前缀有效），则在 current 后加 ‘)’，递归时 right 加 1

编写代码：

class Solution {vector<string> ans;string path;
public:void dfs(int left , int right , int n){if(right == n){ans.push_back(path);return;}if(left < n){path += '(';dfs(left+1,right,n);path.pop_back();}if(left > right){path += ')';dfs(left,right+1,n);path.pop_back();}}vector<string> generateParenthesis(int n) {dfs(0,0,n);return ans;}
};

---

五、组合

题目描述：

思路讲解：
本道题需要我们返回范围 [1, n] 中所有可能的 k 个数的组合。以下是具体思路：

• 全局变量：
  • path：当前正在构建的组合
  • ans：存储所有符合条件的组合
• 终止条件：
  • 当path的长度等于 k 时，说明已生成一个有效组合，将其加入ans并返回
• 递归逻辑：
  • 从pos开始遍历到 n，选择每个数作为组合的下一个元素
  • 选择元素i后，将其加入path，并递归选择下一个元素（起始位置为i+1，确保递增）
  • 递归返回后，继续选择下一个数

编写代码：

class Solution {vector<vector<int>> ans;vector<int> path;
public:void _combine(int n, int k, int pos) {if(k == 0){ans.push_back(path);return;}for(int i = pos ; i <= n ; i++){path.push_back(i);_combine(n,k-1,i+1);path.pop_back();}}vector<vector<int>> combine(int n, int k) {_combine(n,k,1);return ans;}
};

---

六、目标和

题目描述：

思路讲解：
本道题需要我们根据整数数组 nums 构造表达式，获取表达式结果等于target的表达式的个数。对于数组中的每个数字，有两种选择：添加 “+”（加上当前数字值）或添加 “-”（减去该值）。通过递归遍历所有可能的符号组合，计算表达式值结果，统计等于 target 的情况。以下是具体思路：

• 全局变量：
  • ans：统计满足要求表达式的总数量
• 函数参数：
  • nums：原始数组
  • target：目标结果
  • pos：当前处理的数字索引
  • cur：当前表达式的累计结果
• 终止条件：
  • 当index等于数组长度时，若cur等于target，则ans加 1，否则不计数，直接返回
• 递归逻辑：
  • 处理第pos个数字时，分两种情况递归：
    • 给当前数字加 “+”：cur + nums[pos]，递归处理下一个数字（pos + 1）
    • 给当前数字加 “-”：cur - nums[pos]，递归处理下一个数字（pos + 1）

编写代码：

class Solution {int ans;
public:void _findTargetSumWays(vector<int>& nums, int target , int cur , int pos) {if(pos == nums.size()){if(cur == target){ans += 1;}return;}_findTargetSumWays(nums,target,cur+nums[pos],pos+1);_findTargetSumWays(nums,target,cur-nums[pos],pos+1);}int findTargetSumWays(vector<int>& nums, int target) {_findTargetSumWays(nums,target,0,0);return ans;}
};

---

七、组合总和

题目描述：

思路讲解：
本道题需要我们根据整数数组 candidates 中的数，找出组合中元素和为目标整数 target的组合个数，元素可无限制重复选取，但组合不能重复。以下是具体思路：

• 全局变量：
  • path：当前正在构建的组合
  • ans：存储所有符合条件的组合
• 函数参数：
  • candidates：无重复元素的数组
  • target：目标和
  • pos：当前选择的起始索引
  • cur：当前组合的累计和
• 终止条件：
  • 若cur == target：将path加入ans并返回
  • 若cur > target：当前组合已超过目标和，直接返回
• 递归逻辑：
  • 从pos开始遍历数组元素
  • 选择元素candidates[i]：将其加入path，更新cur
  • 由于元素可重复选取，下一次选择仍从i开始
  • 递归返回后，从path中移除该元素，恢复cur，继续尝试下一个元素

编写代码：

class Solution {vector<vector<int>> ans;vector<int> path;int size;
public:void _combinationSum(vector<int>& candidates, int target , int pos, int cur) {if(cur >= target){if(cur == target)ans.push_back(path);return;}for(int i = pos ; i < size ; i++){path.push_back(candidates[i]);_combinationSum(candidates,target,i,cur+candidates[i]);path.pop_back();}}vector<vector<int>> combinationSum(vector<int>& candidates, int target) {size = candidates.size();_combinationSum(candidates,target,0,0);return ans;}
};

---

八、字母大小写全排列

题目描述：

思路讲解：
将字符串中的某个字母转变大小写，这样可以获得一个新的字符串，本道题需要我们将字符串中的每个字母转变大小写，返回能得到的字符串集合 。通过遍历字符串每个位置，对字母进行大小写转换的所有可能尝试，生成所有排列。以下是具体思路：

• 全局变量：
  • ans：存储所有符合条件的字符串
• 函数参数：
  • s：当前处理的字符串
  • pos：当前处理的字符位置
• 终止条件：
  • 当 pos 等于字符串长度时，说明已处理完所有字符，将当前字符串 s 加入结果集 ans 并返回
• 递归逻辑：
  • 不修改当前字符：直接递归处理下一个位置（pos + 1），保持当前字符不变
  • 修改当前字符：
    • 若为小写字母（a-z）：转换为大写（ASCII 码减 32），递归处理下一个位置
    • 若为大写字母（A-Z）：转换为小写（ASCII 码加 32），递归处理下一个位置
  • 非字母字符（如数字、符号）：仅执行 “不修改” 分支，无大小写转换

编写代码：

class Solution {vector<string> ans;
public:void dfs(string s , int pos){if(pos == s.size()){ans.push_back(s);return;}dfs(s,pos+1);if('a' <= s[pos] && s[pos] <= 'z'){s[pos] -= 32;dfs(s,pos+1);}else if('A' <= s[pos] && s[pos] <= 'Z'){s[pos] += 32;dfs(s,pos+1);}}vector<string> letterCasePermutation(string s) {dfs(s,0);return ans;}
};

---

九、优美的排列

题目描述：

思路讲解：
本道题需要我们根据一个整数 n ，返回可以构造的优美排列的数量。通过回溯法尝试在每个位置放置符合条件的数字，统计所有可能的优美排列数量。以下是具体思路：

• 全局变量：
  • ans：统计优美排列的总数量
  • isuse：标记数字是否已被使用
• 函数参数：
  • n：整数范围上限
  • pos：当前要填充的位置
• 终止条件：
  • 当 pos 等于 n + 1 时，说明所有位置（1 到 n）都已填充完毕，构成一个有效排列，因此 ans 加 1 并返回
• 递归逻辑：
  • 遍历 1 到 n 的所有整数，对每个未使用的数字 i：
    • 检查是否满足优美排列条件：pos 能被 i 整除 或 i 能被 pos 整除
    • 若满足条件：标记 i 为已使用，递归处理下一个位置（pos + 1）
    • 递归返回后，回溯：将 i 标记为未使用，继续尝试其他数字

编写代码：

class Solution {bool isuse[16];int ans = 0;
public:void dfs(int n , int pos){if(pos == n + 1) {ans++;return;}for(int i = 1 ; i <= n ; i++){if((pos % i == 0 || i % pos == 0) && isuse[i] == false){isuse[i] = true;dfs(n , pos + 1);isuse[i] = false;}}}int countArrangement(int n) {dfs(n , 1);return ans;}
};

---

十、N 皇后

题目描述：

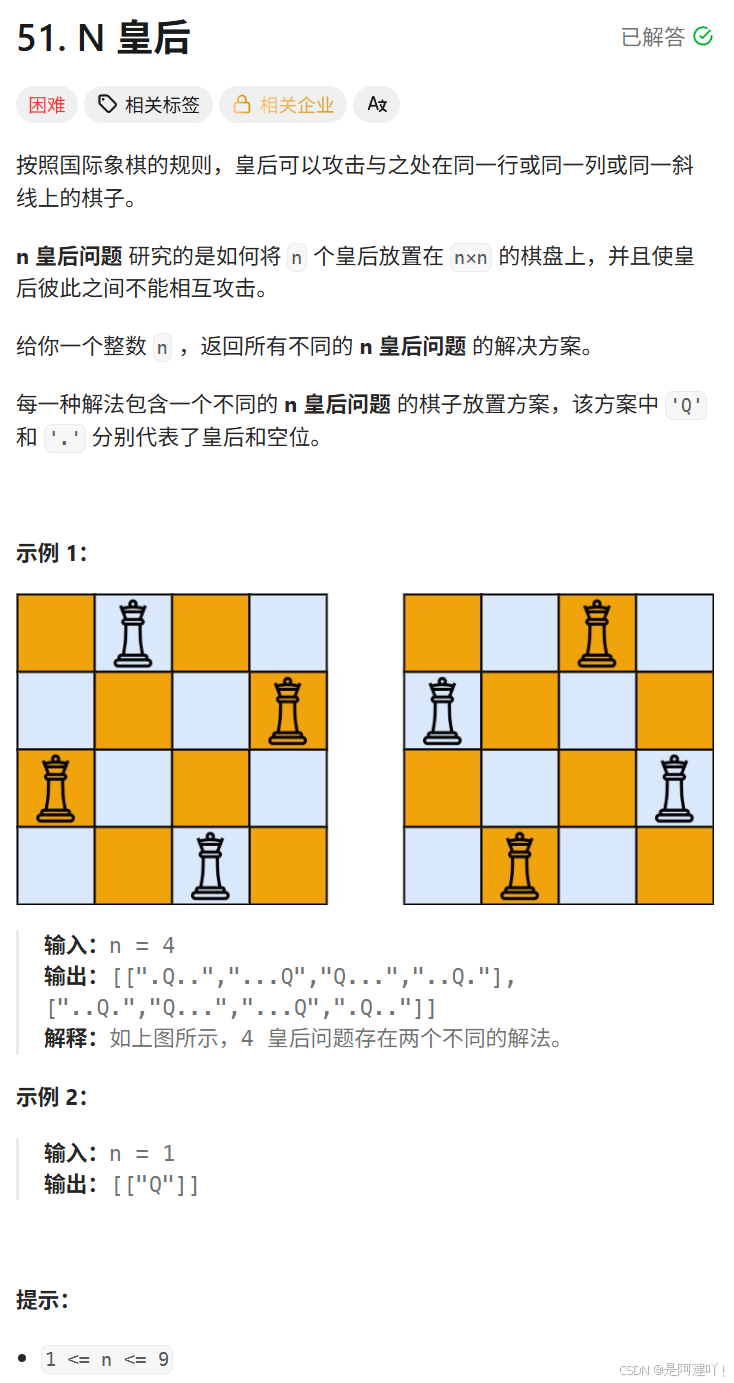
思路讲解：
本道题需要我们找到n*n中n个皇后的摆放问题，皇后不能处于同一行、同一列或同一斜线（包括正斜线和反斜线），所以本道题核心问题就是判断皇后是否与其他皇后处于同一行、同一列或同一斜线。这里先讲述一下如何判断是否在同一斜线，我们将每一个格子想象为一个点 ，当为正斜线时，根据 y = x + b 可以推断出 y - x = b，也就是说当两个点的纵坐标 - 横坐标的值相等，那么这两个点就处于同一条斜线，同理当为反斜线时，根据 y = -x + b 可以推断出 y + x = b，也是就说两个点的纵坐标 + 横坐标的值相等，那么这两个点就在同一条斜线。

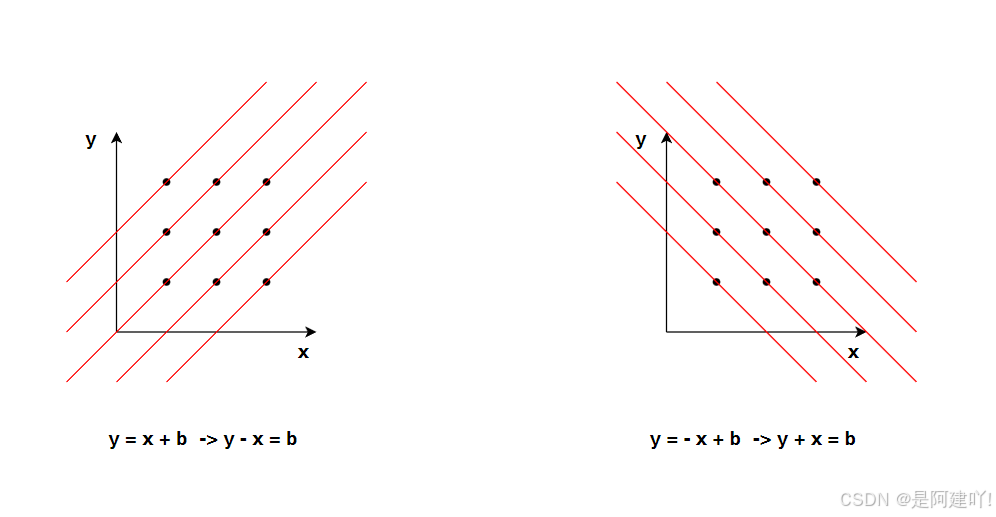
以下是本道题具体思路：

• 函数参数：
  • n：棋盘大小
  • col：当前要放置皇后的列
• 全局变量：
  • path：当前棋盘状态
  • row_used：标记行是否已放置皇后
  • isuse1：标记正斜线是否已有皇后
  • isuse2：标记反斜线是否已有皇后
  • ans：存储所有合法的摆放方案
• 终止条件：
  • 当 col == n 时，说明所有列都已成功放置皇后，将当前棋盘状态 path 加入结果集 ans 并返回
• 递归逻辑：
  • 遍历当前列（col）的每一行（i），检查是否可以放置皇后：
    • 若当前行、正斜线、反斜线均未被占用：
      • 在 path[i][col] 放置皇后（‘Q’）
      • 标记对应的行和斜线为已使用
      • 递归处理下一列（col + 1）
      • 撤销当前皇后的放置（恢复为 ‘.’），并重置辅助数组的标记

编写代码：

class Solution {vector<vector<string>> ans;vector<string> path;bool isuse1[20];bool isuse2[20];bool row_used[10];
public:void dfs(int n , int col){if(col == n){ans.push_back(path);return;}for(int i = 0 ; i < n ; i++){if(row_used[i] == false && isuse1[i-col+n] == false && isuse2[i+col] == false){path[i][col] = 'Q';row_used[i] = true;isuse1[i-col+n] = true;isuse2[i+col] = true;dfs(n,col+1);path[i][col] = '.';row_used[i] = false;isuse1[i-col+n] = false;isuse2[i+col] = false;}}}vector<vector<string>> solveNQueens(int n) {string str;for(int i = 0 ; i < n ; i++)str += '.';for(int i = 0 ; i < n ; i++)path.push_back(str);dfs(n,0);return ans;}
};

---

十一、有效的数独

题目描述：

思路讲解：
本道题需要我们判断数独的有效性，本道题通过迭代遍历 + 哈希标记的方式验证数独有效性，使用三个辅助数组标记当前数字是否在在当前行、列、3x3 宫中出现，以下是具体思路：

• 全局变量：
  • rows_used：rows_used[i][num] 标记第 i 行中数字 num 是否已出现（第一维为行索引 0-8，第二维为数字 1-9）
  • cols_used：cols_used[num][j] 标记第 j 列中数字 num 是否已出现（第一维为数字 1-9，第二维为列索引 0-8）
  • block_used：block_used[x][y][num] 标记第 (x,y) 个 3x3 宫内数字 num 是否已出现（x = i/3，y = j/3，对应 3x3 宫的行和列索引 0-2）
• 遍历整个数独棋盘：
  • 两层循环遍历 9x9 棋盘的每个单元格 (i,j)（i 为行索引，j 为列索引）
• 处理数字：
  • 若单元格内容为数字，将其转换为整数 num
• 检查重复冲突：
  • 若 rows_used[i][num] 为 true：第 i 行已出现 num，返回无效
  • 若 cols_used[num][j] 为 true：第 j 列已出现 num，返回无效
  • 若 block_used[i/3][j/3][num] 为 true：当前 3x3 宫已出现 num，返回无效
• 标记数字使用状态：
  • 若未冲突，则将上述三个数组中对应位置标记为 true，记录该数字已出现
• 遍历完成：
  • 若所有单元格均无冲突，返回有效（true）

编写代码：

class Solution {bool rows_used[10][10];bool cols_used[10][10];bool block_used[3][3][10];
public:bool isValidSudoku(vector<vector<char>>& board) {for (int i = 0; i < 9; i++) {for (int j = 0; j < 9; j++) {int num = board[i][j] - '0';if (board[i][j] != '.'){if((rows_used[i][num] || cols_used[num][j] || block_used[i/3][j/3][num]))return false;rows_used[i][num] = true;cols_used[num][j] = true;block_used[i/3][j/3][num] = true;}}}return true;}
};

---

十二、解数独

题目描述：

思路讲解：
本道题需要我们填充空格来解决数独问题，首先使用三个辅助数组标记已在数组中出现的数字是否在在当前行、列、3x3 宫中出现，再找到数独的空白格，通过回溯法尝试为每个空格填充合法数字，并利用辅助数组确保符合数独规则，以下是具体思路：

• 全局变量：
  • rows_used：rows_used[i][num] 标记第 i 行中数字 num 是否已出现（第一维为行索引 0-8，第二维为数字 1-9）
  • cols_used：cols_used[num][j] 标记第 j 列中数字 num 是否已出现（第一维为数字 1-9，第二维为列索引 0-8）
  • block_used：block_used[x][y][num] 标记第 (x,y) 个 3x3 宫内数字 num 是否已出现（x = i/3，y = j/3，对应 3x3 宫的行和列索引 0-2）
• 初始化准备：
  • 遍历数独初始状态，将已填充的数字对应的辅助数组位置标记为true，为递归填充做准备
• 终止条件：
  • 当遍历完所有单元格，返回true
• 递归逻辑：
  • 两层循环遍历棋盘，找到第一个空白格（board[row][col] = ‘.’）
  • 对 1-9 的每个数字num，检查是否符合行、列、宫格约束
  • 选择与递归：
    • 若数字num合法，填充到空白格，并更新辅助数组标记为true
    • 若返回true，说明当前填充可通向解，直接返回true
    • 若递归返回false，撤销当前填充（恢复为 ‘.’），重置辅助数组，尝试下一个数字
  • 若 1-9 均无法填入当前空白格，返回false，回溯到上一层

编写代码：

class Solution {bool row_used[10][10];bool col_used[10][10];bool block_used[3][3][10];public:bool dfs(vector<vector<char>>& board){for(int row = 0 ; row < 9 ; row++){for(int col = 0 ; col < 9 ; col++){if(board[row][col] == '.'){for(int num = 1 ; num <= 9 ; num++){if(row_used[row][num] == false && col_used[num][col] == false && block_used[row/3][col/3][num] == false){board[row][col] = num + '0';row_used[row][num] = col_used[num][col] = block_used[row/3][col/3][num] = true;if(dfs(board) == false){row_used[row][num] = col_used[num][col] = block_used[row/3][col/3][num] = false;continue;}return true;}}board[row][col] = '.';return false;}}}return true;}void solveSudoku(vector<vector<char>>& board) {for(int i = 0 ; i < 9 ; i++){for(int j = 0 ; j < 9 ; j++){if(board[i][j] != '.'){int num = board[i][j] - '0';row_used[i][num] = col_used[num][j] = block_used[i/3][j/3][num] = true;}}}dfs(board);}
};

---

十三、单词搜索

题目描述：

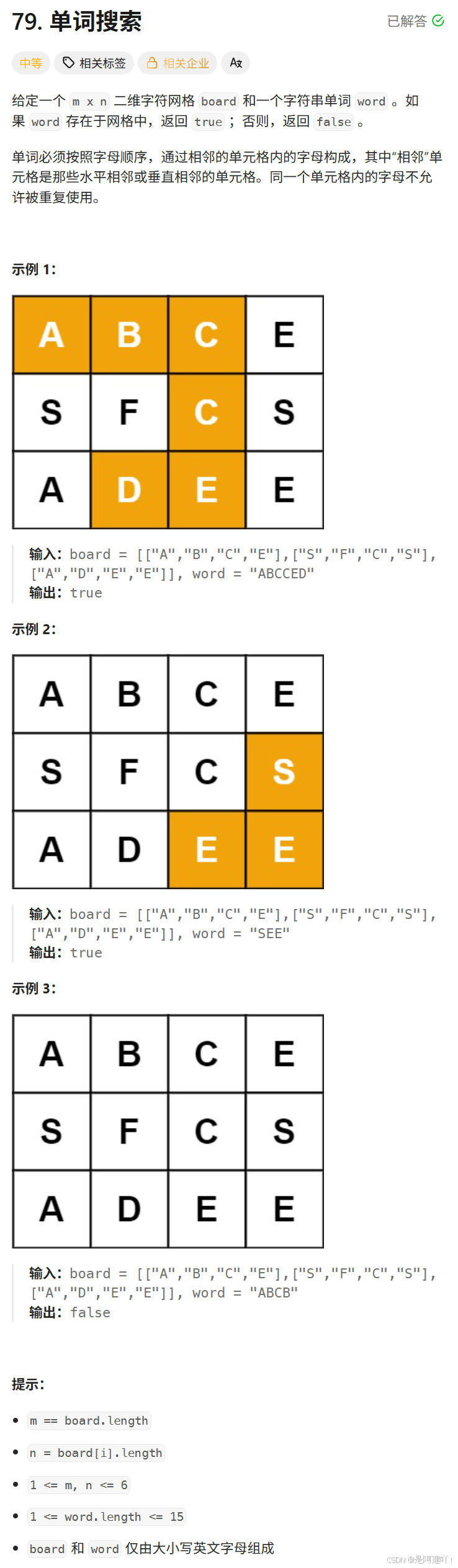
思路讲解：
本道题需要我们根据给定的 m x n 二维字符网格，判断是否通过相邻的单元格内的字母构成字符串单词 word 。可以从与单词首字母匹配的单元格开始，向上下左右四个方向递归探索，依次匹配单词的每个后续字母，确保路径连续且单元格不重复使用。以下是具体思路：

• 函数参数：
  • board：二维字符网格
  • word：目标单词
  • row，col：当前探索的起始网格坐标
  • curpos：当前需要匹配的单词字符索引
• 全局变量：
  • vis：标记单元格是否已访问的二维数组
  • dx，dy：方向数组，代表右、左、上、下四个移动方向
• 终止条件：
  • 当 curpos 等于单词长度时，说明所有字符已匹配成功，返回 true
• 递归逻辑：
  • 遍历四个方向，计算新坐标 (x,y)，对其进行合法性检查：
    • 处于网格边界内（0 <= x < rows 且 0 <=y < cols）
    • 未被访问过（vis[x][y] = false）
    • 字符与单词 curpos 位置的字符匹配（board[x][y] == word[curpos]）
  • 若满足条件：
    • 标记 (x,y) 为已访问（vis[x][y] = true）
    • 递归探索下一个字符（curpos + 1），若递归返回 true，则当前路径有效，直接返回 true
    • 若递归失败，取消 (x,y) 的访问标记（vis[x][y] = false），继续尝试其他方向
  • 若所有方向均匹配失败，返回 false
• 初始启动：
  • 遍历网格，找到与单词首字母（word[0]）匹配的单元格，标记其为已访问后，启动 DFS 递归

编写代码：

class Solution {int dx[4] = {0,0,-1,1};int dy[4] = {1,-1,0,0};int rows , cols;bool vis[7][7];
public:bool dfs(vector<vector<char>>& board, string& word , int row , int col ,int curpos) {if(curpos == word.size())return true;for(int i = 0 ; i < 4 ; i++){int x = row + dx[i];int y = col + dy[i];if(0 <= x && x < rows && 0 <= y && y < cols && board[x][y] == word[curpos] && vis[x][y] == false){vis[x][y] = true;if(dfs(board,word,x,y,curpos+1)) return true;vis[x][y] = false;}}return false;}bool exist(vector<vector<char>>& board, string word) {rows = board.size() , cols = board[0].size();for(int i = 0 ; i < rows ; i++){for(int j = 0 ; j < cols ; j++){if(board[i][j] == word[0]){vis[i][j] = true;if(dfs(board,word,i,j,1)) return true;vis[i][j] = false;}}}return false;}
};

---

十四、黄金矿工

题目描述：

思路讲解：
本道题需要我们根据规则找到最多的黄金，我们可以通过从每个有黄金的单元格出发，向四周探索所有可能的开采路径，记录最大黄金收益。以下是具体思路：

• 函数参数：
  • grid：黄金分布的二维网格
  • row，col：当前矿工所在的网格坐标
  • cur：当前开采路径的黄金总和
• 全局变量：
  • vis：标记单元格是否已开采的二维数组
  • dx，dy：方向数组，代表右、左、上、下四个移动方向
  • ans：记录所有路径中的最大黄金收益
• 递归逻辑：
  • 进入递归后，首先将当前路径的黄金总和cur与ans比较，更新ans为较大值
  • 遍历四个方向，计算新坐标(x,y)
  • 坐标合法性检查，新坐标需要满足：
    • 在网格边界内（0 <= x < rows 且 0 <=y < cols）
    • 未被开采过（vis[x][y] = false）
  • 递归开采：
    • 标记新坐标为已开采（vis[x][y] = true）
    • 递归探索该方向，更新当前黄金总和（cur + grid[x][y]）
    • 递归返回后，取消新坐标的开采标记（vis[x][y] = false），尝试其他方向
• 初始探索：
  • 遍历网格所有单元格，若单元格有黄金，则以此为起点调用递归函数

编写代码：

class Solution {int dx[4] = {0,0,-1,1};int dy[4] = {1,-1,0,0};int ans = 0 ;int rows , cols;bool vis[16][16];
public:void dfs(vector<vector<int>>& grid , int row , int col , int cur) {ans = max(ans,cur);if(grid[row][col] == 0) return;for(int i = 0 ; i < 4 ; i++){int x = row + dx[i] , y = col + dy[i];if(0 <= x && x < rows && 0 <= y && y < cols && vis[x][y] == false){vis[x][y] = true;dfs(grid,x,y,cur+grid[x][y]);vis[x][y] = false;}}}int getMaximumGold(vector<vector<int>>& grid) {rows = grid.size() , cols = grid[0].size();for(int i = 0 ; i < rows ; i++){for(int j = 0 ; j < cols ; j++){if(grid[i][j] != 0){vis[i][j] = true;dfs(grid,i,j,grid[i][j]);vis[i][j] = false;}}}return ans;}   
};

---

十五、不同路径 III

题目描述：

思路讲解：
本道题需要我们找出从起点到终点的所有路径，需要保证每一个无障碍方格都要通过一次。本道题可以通过采用深度优先搜索递归思路，通过统计空方格总数并校验路径长度，高效统计从起点到终点且经过所有无障碍方格的路径数目，以下是具体思路：

• 全局变量：
  • rows，cols：网格的行数和列数
  • cnt：空方格的总数
  • path：当前路径的长度
  • ans：符合条件的路径总数
  • dx，dy：方向数组，表示上下左右四个移动方向
• 函数参数：
  • grid：原始网格
  • vis：标记方格是否已访问的二维数组
  • row，col：当前所在的网格坐标
• 初始准备：
  • 遍历网格，定位起点坐标（grid[i][j] == 1）
  • 统计空方格总数 cnt（grid[i][j] == 0 的数量）
  • 初始化路径长度 path 为 1（起点已被计入路径），并标记起点为已访问
• 递归逻辑：
  • 当当前方格为终点（grid[row][col] == 2）时，检查路径长度是否满足 path == cnt + 2：
  • 若满足条件，说明所有无障碍方格均已遍历，ans 计数加 1；否则路径无效，直接返回
  • 遍历四个方向，计算新坐标 (x, y)，检查其合法性：
    • 处于网格边界内（0 <= x < rows 且 0 <= y < cols）
    • 未被访问过（vis[x][y] == false）
    • 不是障碍（grid[x][y] != -1）
  • 递归与回溯：
    • 更新路径长度，标记新坐标为已访问
    • 递归探索该方向的下一个方格
    • 递归返回后，恢复路径长度和访问标记未访问，尝试其他方向

编写代码：

class Solution {int dx[4] = {0,0,-1,1};int dy[4] = {1,-1,0,0};int begin_row , begin_cow , end_row , end_cow;int rows , cols;int cnt = 0 , path = 0;int ans = 0;
public:void dfs(vector<vector<int>>& grid , vector<vector<bool>>& vis ,int row , int col){if(row == end_row && col == end_cow){if(path == cnt + 2)ans++;return;}for(int i = 0 ; i < 4 ; i++){int x = row + dx[i] , y = col + dy[i];if(0 <= x && x < rows && 0 <= y && y < cols && vis[x][y] == false && grid[x][y] != -1){path++;vis[x][y] = true;dfs(grid,vis,x,y);path--;vis[x][y] = false;}}}int uniquePathsIII(vector<vector<int>>& grid) {rows = grid.size() , cols = grid[0].size();vector<vector<bool>> vis(rows,vector<bool>(cols,false));for(int i = 0 ; i < rows ; i++){for(int j = 0 ; j < cols ; j++){if(grid[i][j] == 1){begin_row = i;begin_cow = j;}   else if(grid[i][j] == 2){end_row = i;end_cow = j;}  else if(grid[i][j] == 0){cnt++;}}}path++;vis[begin_row][begin_cow] = true;dfs(grid,vis,begin_row,begin_cow);return ans;}
};

---

结尾

如果有什么建议和疑问，或是有什么错误，大家可以在评论区中提出。
希望大家以后也能和我一起进步！！🌹🌹
如果这篇文章对你有用的话，希望大家给一个三连支持一下！！🌹🌹