当前位置：首页 > news >正文

【DL】浅层神经网络

news 2025/8/16 15:38:17

线性模型

回归，regression，直观理解就是根据过去的一堆数据进行预测。

为了评估回归模型的精度，通常使用均方误差（Mean Squared Error, MSE）或平均绝对误差（Mean Absolute Error, MAE）作为度量标准，这就是所谓的目标函数，有时也叫损失函数。【均方误差是指预测值与真实值之差的平方和的平均数，而平均绝对误差则是指预测值与真实值之差的绝对值的平均数。较低的均方误差或平均绝对误差表明模型的预测精度较高。】

目标函数通常是建立在训练数据集上的，并且在训练过程中不断优化。

优化器：随机梯度下降法

机器学习优化器可以分为基于梯度的优化器和非基于梯度的优化器。

基于梯度的优化器是基于损失函数的梯度来更新模型参数的。常用的基于梯度的优化器包括随机梯度下降（SGD）、动量法（Momentum）、Adagrad、RMSProp和Adam。

非基于梯度的优化器是基于非梯度信息来更新模型参数的。常用的非基于梯度的优化器包括模拟退火法（Simulated Annealing）和遗传算法（Genetic Algorithm）。

最简单的优化器是随机梯度下降（SGD）。它是一种基于梯度的优化器，在每次迭代时使用一个小的训练样本来计算损失函数的梯度。SGD的优点在于它简单易用，但是可能不够稳定，因为它可能会跳出最优解。

神经网络基本原理

神经网络（Neural Network）是一种模拟人脑神经系统功能的计算模型。它由多个节点组成，节点之间通过权重相连，这些节点构成了多个层，每一层节点的输入和输出都是上一层节点的输出，最终输出层的输出即为神经网络的结果。

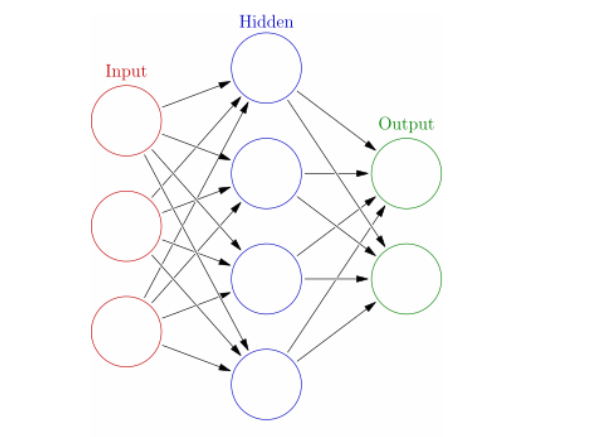
输入层的节点数量等于输入信息的维度，输出层的节点数量等于输出信息的维度。隐藏层的节点数量是由设计者决定的，一般来说，隐藏层节点数量越多，神经网络的表示能力就越强。但同时也要注意，隐藏层节点数量过多会导致训练时间增加，同时也容易导致过拟合。

网络的结构是静态的，但是它的权重是动态的。通过训练，神经网络可以学习输入数据的内在规律，并通过调整权重来改进对输入数据的预测能力。训练过程通常使用反向传播算法（Backpropagation）来实现。这种方法常用于调整神经网络的权重，使得预测的输出与实际的输出尽可能接近。

神经网络中的每个节点都是一个线性模型，它将输入数据乘以权重，然后通过一个非线性激活函数进行转换，最后输出一个值。这样，多个线性模型就组合起来，通过调整每个节点的权重和非线性激活函数，可以学习输入数据的复杂关系。

神经网络的非线性激活函数是神经网络的重要组成部分，它的作用是在输入数据的基础上进行非线性转换，从而使得神经网络具有更强的表示能力。常用的非线性激活函数包括 Sigmoid 函数、Tanh 函数、ReLU 函数和 Leaky ReLU 函数等。

分类问题

多分类问题的数学表示

机器学习算法的套路往往都是先用一个数学模型描述一个问题，然后找到一个目标函数，再用最优化的方法逼近求解得到模型参数。这个过程就是机器学习，也就是训练的过程。

在数学表示中，我们通常使用一个向量来表示输入数据。这个向量通常被称为“特征向量”，并且由输入数据的多个特征构成。

线性模型和Softmax回归

Softmax回归，也被称为多项式逻辑回归，可以输出多个类别的概率。用数学的语言来说，设输入图像的向量表示为x，模型可以写成如下形式：

y^=softmax(Wx+b)

其中W和b是模型参数，也是要学习的变量。W是个矩阵，其中的每一列对应一个特征，每一行对应一个类别。b是一个向量，其中的每一个元素对应一个类别。y^是模型输出，它是一个长度为K的向量，K是类别的数量。每一个元素y^i表示输入图像属于i个类别的概率。我们希望每个元素y^i越大越好，因为这意味着输入图像属于第i个类别的可能性越大。 softmax(⋅)是一个函数，它可以将向量Wx+b中的每一个元素转换为概率值。在多分类问题中使用 Softmax 运算的好处是因为它可以将输入的特征向量转换为概率值，这个概率值更加符合我们的直觉，从而方便进行决策。